1. 小妍将完全相同的圆柱用三种不同的方式进行切分(如图),圆柱的底面直径都是4厘米。
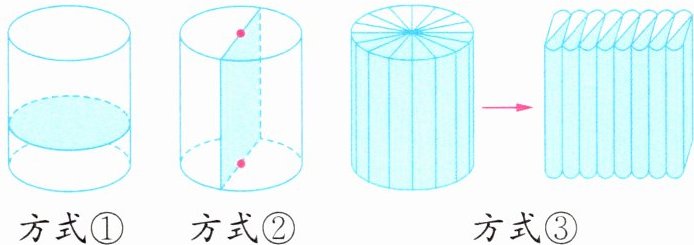
(1) 方式①表面积增加了(
(2) 无论怎样切分,形成的立体图形的体积(或体积和)都是(

(1) 方式①表面积增加了(
25.12
)平方厘米,方式②表面积增加了40平方厘米,方式③表面积增加了(20
)平方厘米。切分之前每个圆柱的表面积都是(87.92
)平方厘米。(2) 无论怎样切分,形成的立体图形的体积(或体积和)都是(
62.8
)立方厘米。答案:1.(1)25.12 20 87.92 (2)62.8
2. 一个圆锥的高和底面半径都等于一个正方体的棱长,已知正方体的体积是60立方厘米,圆锥的体积是(
62.8
)立方厘米。答案:2.62.8 解析 设正方体的棱长为$a$厘米,$a^{3}=60$,因为圆锥的高和底面半径都等于正方体的棱长,即为$a$厘米,那么圆锥的体积就是$3.14 × a^{2} × a × \frac{1}{3}=3.14 × a^{3} × \frac{1}{3}=3.14 × 60 × \frac{1}{3}=62.8$(立方厘米)。
解析:
设正方体的棱长为$a$厘米,由正方体体积是$60$立方厘米,可得$a^{3}=60$。圆锥的高和底面半径都等于正方体的棱长$a$厘米,圆锥体积公式为$\frac{1}{3}\pi r^{2}h$,则圆锥体积为$\frac{1}{3}×3.14× a^{2}× a=\frac{1}{3}×3.14× a^{3}$,将$a^{3}=60$代入,得$\frac{1}{3}×3.14×60 = 62.8$立方厘米。
62.8
62.8
3. 一支未用过的圆柱形铅笔长18 cm,体积是9 cm³。使用一段时间后变成下面的样子,此时铅笔的体积是(

5
)cm³。
答案:3.5 解析 把题图中铅笔的体积看作是等底的高9cm的圆柱与高3cm的圆锥的体积和,根据题意可知高9cm的圆柱体积是原来铅笔体积的$9 ÷ 18=\frac{1}{2}$,就是$9 × \frac{1}{2}=4.5(cm^{3})$),高3cm的圆锥体积是原来铅笔体积的$3 ÷ 18 × \frac{1}{3}=\frac{1}{18}$,就是$9 × \frac{1}{18}=0.5(cm^{3})$,所以此时铅笔的体积是$4.5+0.5=5(cm^{3})$。
解析:
高9cm的圆柱体积是原来铅笔体积的$9÷18=\frac{1}{2}$,即$9×\frac{1}{2}=4.5\ \mathrm{cm}^3$;高3cm的圆锥体积是原来铅笔体积的$3÷18×\frac{1}{3}=\frac{1}{18}$,即$9×\frac{1}{18}=0.5\ \mathrm{cm}^3$;此时铅笔体积为$4.5 + 0.5=5\ \mathrm{cm}^3$。
1. 下面各图形以虚线为轴旋转一周形成一个立体图形,图形(

A
)形成的体积与右图形成的体积相等。

答案:1.A
(2025·南通海门区期末)如图,将棱长
相等的两块正方体木料①、②分别加工
成1个大圆柱和4个相同的小圆柱,剩
下的木料体积相比,结果是( )。

答案:C
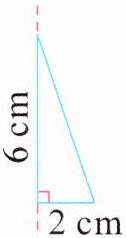
1. 明明用彩纸和小棒做了一面长方形的彩旗(如图)。旋转小棒,观察下图并想象彩旗旋转一周所形成的立体图形,形成的立体图形的蓝色部分和绿色部分的体积分别是多少?(小棒忽略不计)


答案:1.$3.14 × 6^{2} × 5=565.2$(立方厘米)
蓝色部分:$565.2 × \frac{1}{3}=188.4$(立方厘米)
绿色部分:$565.2-188.4=376.8$(立方厘米)
蓝色部分:$565.2 × \frac{1}{3}=188.4$(立方厘米)
绿色部分:$565.2-188.4=376.8$(立方厘米)
2. 一块蛋糕如图,在它的表面涂上奶油(下底面不涂),需要涂多少平方厘米的奶油? 这块蛋糕的体积是多少立方厘米?


答案:2.$3.14 × 10^{2} × \frac{1}{4}+3.14 × 10 × 2 × 8 × \frac{1}{4}+10 × 8 × 2=364.1$(平方厘米) $3.14 × 10^{2} × 8 × \frac{1}{4}=628$(立方厘米)
解析:
涂奶油面积:$3.14×10^{2}×\frac{1}{4}+3.14×10×2×8×\frac{1}{4}+10×8×2=364.1$(平方厘米)
体积:$3.14×10^{2}×8×\frac{1}{4}=628$(立方厘米)
体积:$3.14×10^{2}×8×\frac{1}{4}=628$(立方厘米)