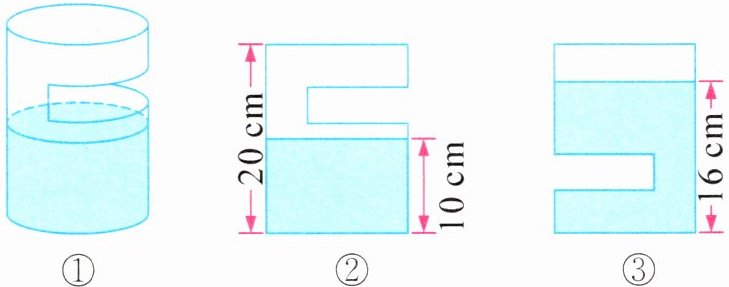
8. 有一玻璃密封器皿中有一些水,如图①,测得器皿高为 20 厘米。如图②放置时,测得液面高 10 厘米;如图③放置时,测得液面高 16 厘米,容器中水的体积占容器容积的(
$\frac{5}{7}$
)。
答案:8. $\frac{5}{7}$
解析:
设圆柱底面积为$S$,容器容积为$V$,水的体积为$V_{水}$。
由图②:$V_{水}=10S$。
由图③:无水部分体积为$(20 - 16)S=4S$,则$V_{水}=V - 4S$。
因为$V = 20S$,所以$10S=20S - 4S$,解得$V_{水}=10S$,$V = 14S$。
$\frac{V_{水}}{V}=\frac{10S}{14S}=\frac{5}{7}$。
$\frac{5}{7}$
由图②:$V_{水}=10S$。
由图③:无水部分体积为$(20 - 16)S=4S$,则$V_{水}=V - 4S$。
因为$V = 20S$,所以$10S=20S - 4S$,解得$V_{水}=10S$,$V = 14S$。
$\frac{V_{水}}{V}=\frac{10S}{14S}=\frac{5}{7}$。
$\frac{5}{7}$
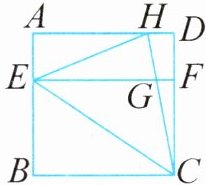
9. 如图,正方形 ABCD 的边长为 4 cm,EF 和 BC 平行,三角形 ECH 的面积是 7 cm²,EG 的长为(
3.5
)cm。
答案:9. 3.5
解析:
证明:设$EG = x$,$GF = y$,则$EF = x + y$。
因为$EF // BC$,正方形$ABCD$边长为$4$,所以$\triangle ECH$的面积可表示为$\frac{1}{2} × EF × 4 - \frac{1}{2} × GF × 4$。
即$\frac{1}{2} × (x + y) × 4 - \frac{1}{2} × y × 4 = 7$,化简得$2(x + y) - 2y = 7$,$2x = 7$,解得$x = \frac{7}{2} = 3.5$。
故$EG$的长为$3.5$cm。
因为$EF // BC$,正方形$ABCD$边长为$4$,所以$\triangle ECH$的面积可表示为$\frac{1}{2} × EF × 4 - \frac{1}{2} × GF × 4$。
即$\frac{1}{2} × (x + y) × 4 - \frac{1}{2} × y × 4 = 7$,化简得$2(x + y) - 2y = 7$,$2x = 7$,解得$x = \frac{7}{2} = 3.5$。
故$EG$的长为$3.5$cm。
10. 王叔叔是建筑工人,不下雨时他每天的工资是 280 元,雨天时他每天的工资是 180 元。他四月份一天都没有休息,共得工资 7400 元,这个月雨天有(
10
)天。答案:10. 10
解析:
设这个月雨天有$x$天,则不下雨的天数为$(30 - x)$天。
根据题意可列方程:$180x + 280(30 - x) = 7400$
展开括号:$180x + 8400 - 280x = 7400$
移项合并同类项:$-100x = 7400 - 8400$
计算得:$-100x = -1000$
解得:$x = 10$
10
根据题意可列方程:$180x + 280(30 - x) = 7400$
展开括号:$180x + 8400 - 280x = 7400$
移项合并同类项:$-100x = 7400 - 8400$
计算得:$-100x = -1000$
解得:$x = 10$
10
11. 要把 1 米长的铜管锯成 54 毫米和 76 毫米两种规格的铜管,每锯一次都要损耗 1 毫米的铜管,只有当锯得的 54 毫米的铜管为(
7
)段,76 毫米的铜管为(8
)段时,才能使损耗的铜管最少。答案:11. 7 8 解析:设54毫米的有a段,76毫米的有b段,1米=1000毫米。可列出等式54a+76b+(a+b−1)×1=1000,可求出5a+7b=91,a,b都是自然数,试算可知,①a=0,b=13时,式子成立,但题中要求锯成两种规格,所以此方案不合适;②a=7,b=8时,损耗7+8−1=14(毫米);③a=14,b=3时,损耗14+3−1=16(毫米),14<16,则a=7,b=8时,损耗的铜管最少。
解析:
设54毫米的铜管有$a$段,76毫米的铜管有$b$段,1米=1000毫米。
根据题意,损耗的铜管长度为$(a + b - 1)$毫米,可列出方程:
$54a + 76b + (a + b - 1) = 1000$
化简得:
$55a + 77b = 1001$
两边同时除以11:
$5a + 7b = 91$
因为$a$、$b$为自然数,求解方程$5a + 7b = 91$:
当$b = 8$时,$5a = 91 - 7×8 = 91 - 56 = 35$,解得$a = 7$;
当$b = 3$时,$5a = 91 - 7×3 = 91 - 21 = 70$,解得$a = 14$。
计算两种情况下的损耗:
当$a = 7$,$b = 8$时,损耗为$7 + 8 - 1 = 14$毫米;
当$a = 14$,$b = 3$时,损耗为$14 + 3 - 1 = 16$毫米。
因为$14 < 16$,所以当$a = 7$,$b = 8$时损耗最少。
7
8
根据题意,损耗的铜管长度为$(a + b - 1)$毫米,可列出方程:
$54a + 76b + (a + b - 1) = 1000$
化简得:
$55a + 77b = 1001$
两边同时除以11:
$5a + 7b = 91$
因为$a$、$b$为自然数,求解方程$5a + 7b = 91$:
当$b = 8$时,$5a = 91 - 7×8 = 91 - 56 = 35$,解得$a = 7$;
当$b = 3$时,$5a = 91 - 7×3 = 91 - 21 = 70$,解得$a = 14$。
计算两种情况下的损耗:
当$a = 7$,$b = 8$时,损耗为$7 + 8 - 1 = 14$毫米;
当$a = 14$,$b = 3$时,损耗为$14 + 3 - 1 = 16$毫米。
因为$14 < 16$,所以当$a = 7$,$b = 8$时损耗最少。
7
8
1. 六年级一班男生人数是女生人数的$\frac{2}{7}$,已知六年级一班人数在 50~60 之间,六年级一班有女生(
A.42
B.12
C.18
D.40
A
)人。A.42
B.12
C.18
D.40
答案:1. A
解析:
设女生人数为$x$,则男生人数为$\frac{2}{7}x$,总人数为$x+\frac{2}{7}x=\frac{9}{7}x$。
因为人数必须为整数,所以$x$是7的倍数。
总人数在50~60之间,即$50<\frac{9}{7}x<60$,解得$\frac{350}{9}<x<\frac{420}{9}$,约$38.89<x<46.67$。
7的倍数在该范围内的是42,所以女生人数为42人。
A
因为人数必须为整数,所以$x$是7的倍数。
总人数在50~60之间,即$50<\frac{9}{7}x<60$,解得$\frac{350}{9}<x<\frac{420}{9}$,约$38.89<x<46.67$。
7的倍数在该范围内的是42,所以女生人数为42人。
A
2. 对生活中数的估计,最合理的是(
A.六年级数学课本的封面大约是 500 cm²
B.六年级学生的跑步速度大约是 0.75 米/秒
C.一个六年级学生的体重约是 0.5 吨
D.一台家用冰箱的容积大约是 10000 mL
A
)。A.六年级数学课本的封面大约是 500 cm²
B.六年级学生的跑步速度大约是 0.75 米/秒
C.一个六年级学生的体重约是 0.5 吨
D.一台家用冰箱的容积大约是 10000 mL
答案:2. A
3. 新情境 真实生活 某小区投放了甲、乙两种品牌的共享汽车,甲品牌投放的共享汽车的数量占总数的$\frac{5}{8}$,后来甲品牌又投放了 30 辆,这时甲品牌共享汽车的数量正好是乙品牌共享汽车数量的 2 倍,这个小区现在甲、乙两种品牌的共享汽车共投放了(
A.200
B.210
C.270
D.240
C
)辆。A.200
B.210
C.270
D.240
答案:3. C
解析:
设小区最初投放共享汽车总数为$x$辆。
甲品牌最初数量:$\frac{5}{8}x$,乙品牌最初数量:$x - \frac{5}{8}x=\frac{3}{8}x$。
甲品牌投放30辆后数量:$\frac{5}{8}x + 30$。
由题意得:$\frac{5}{8}x + 30 = 2×\frac{3}{8}x$
解得:$x = 240$
现在总数:$240 + 30 = 270$
C
甲品牌最初数量:$\frac{5}{8}x$,乙品牌最初数量:$x - \frac{5}{8}x=\frac{3}{8}x$。
甲品牌投放30辆后数量:$\frac{5}{8}x + 30$。
由题意得:$\frac{5}{8}x + 30 = 2×\frac{3}{8}x$
解得:$x = 240$
现在总数:$240 + 30 = 270$
C
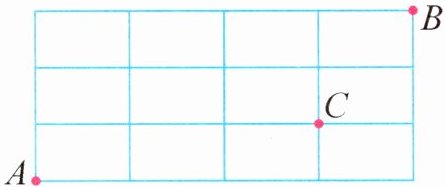
4. 如图,明明从家所在的 A 点去学校所在的 B 点,但途中不能经过 C 点的商店,不同的最短路线一共有(
A.20
B.23
C.30
D.35
B
)条。
A.20
B.23
C.30
D.35
答案:
4. B 解析:如图,根据标数法,可得共有23条最短路线。
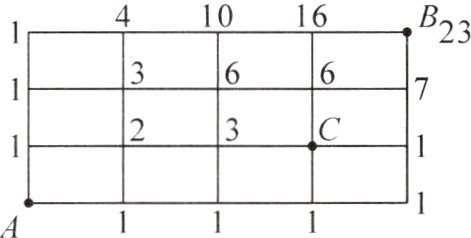
4. B 解析:如图,根据标数法,可得共有23条最短路线。

5. 根据中国传统礼仪,给客人倒水时应倒满茶杯的 70%~80%,如图中的一壶水最多可以倒(
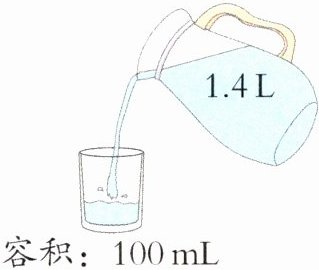
A.14
B.17.5
C.30
D.20
D
)杯。
A.14
B.17.5
C.30
D.20
答案:5. D
解析:
1.4L=1400mL
1400÷(100×70%)=20
D
1400÷(100×70%)=20
D
1. 请分别表示出下图的 50%和 0.5 m。(2 分)


答案:
1.
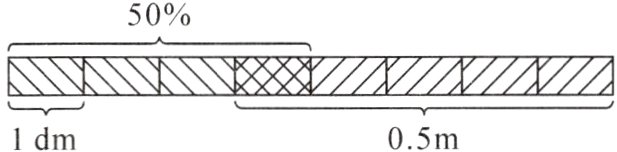
1.

2. 方格图中每个小方格的边长表示 300 米。
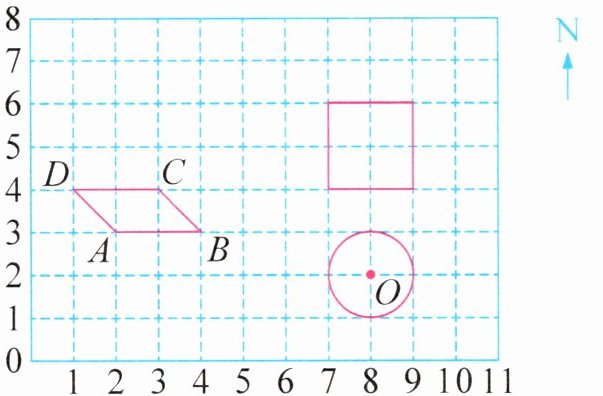
(1)点 A 在点 C 的()偏()()°方向。(3 分)
(2)画出图中平行四边形绕点 B 逆时针旋转 90°后的图形,旋转后 A、C、D 三点的位置用数对表示分别是 A( , ),C( , ),D( , )。(4 分)
(3)把圆向北平移 1 格,平移后圆心 O 与点 B 的实际距离是()米,平移后的圆与正方形组成的图形有()条对称轴。(2 分)

(1)点 A 在点 C 的()偏()()°方向。(3 分)
(2)画出图中平行四边形绕点 B 逆时针旋转 90°后的图形,旋转后 A、C、D 三点的位置用数对表示分别是 A( , ),C( , ),D( , )。(4 分)
(3)把圆向北平移 1 格,平移后圆心 O 与点 B 的实际距离是()米,平移后的圆与正方形组成的图形有()条对称轴。(2 分)
答案:2. (1)南 西 45 (2)画图略 (4,1)
(3,2) (3,0) (3)1200 1
(3,2) (3,0) (3)1200 1