1. 意大利著名数学家斐波那契在研究兔子繁殖问题时,发现了这样一组数:1,1,2,3,5,8,13,…计算 $1^{2}+2^{2}+3^{2}+5^{2}+8^{2}+13^{2}$ 这样的算式时有简便方法吗?明明遇到这个问题时,想到用“数形结合”的方法来探索,于是他以这组数中各个数作为正方形的边长构造正方形,再拼在一起进行研究。
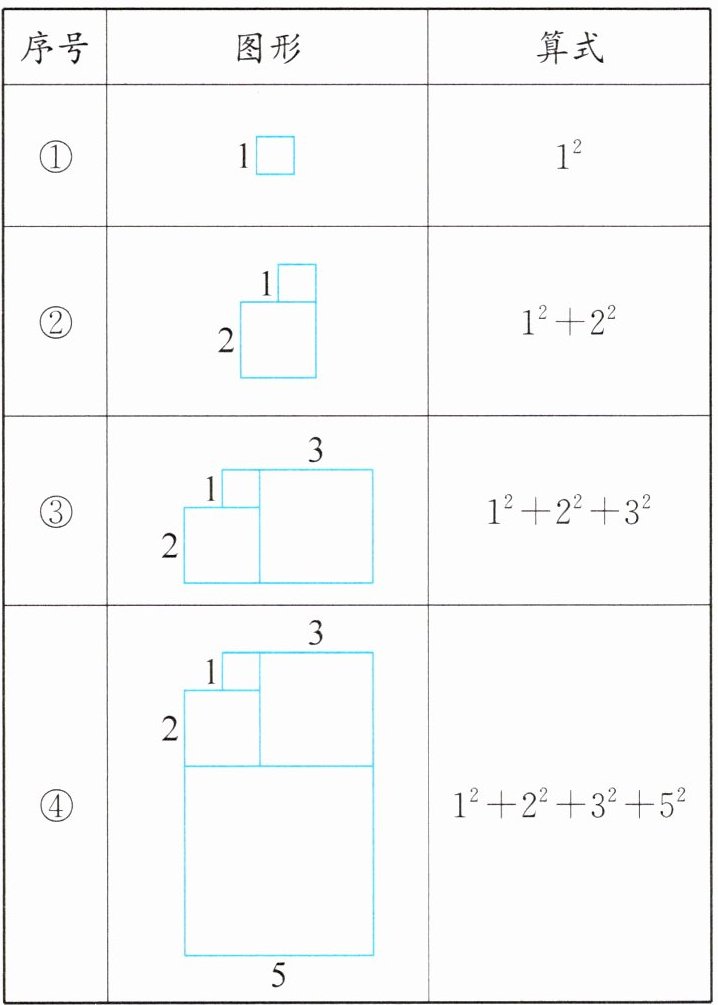
(1)观察上面的图形和算式,把下面的算式补充完整。
$1^{2}=1×2 - 1$
$1^{2}+2^{2}=2×3 - 1$
$1^{2}+2^{2}+3^{2}=(\quad)×(\quad) - 1$
$1^{2}+2^{2}+3^{2}+5^{2}=(\quad)×(\quad) - 1$
$1^{2}+2^{2}+3^{2}+5^{2}+8^{2}+13^{2}=(\quad)×(\quad) - 1$
(2)若按此规律继续拼图形,则序号为(

(1)观察上面的图形和算式,把下面的算式补充完整。
$1^{2}=1×2 - 1$
$1^{2}+2^{2}=2×3 - 1$
$1^{2}+2^{2}+3^{2}=(\quad)×(\quad) - 1$
$1^{2}+2^{2}+3^{2}+5^{2}=(\quad)×(\quad) - 1$
$1^{2}+2^{2}+3^{2}+5^{2}+8^{2}+13^{2}=(\quad)×(\quad) - 1$
(2)若按此规律继续拼图形,则序号为(
⑦
)的图形面积是 713。答案:1.(1)3 5 5 8 13 21 (2)⑦ 解析:观察图形和算式发现,拼成的图形可看成一个长方形减去一个边长为1的正方形,假设补上一个边长为1的正方形,这个图形就成为一个长方形,长方形的宽等于这一列数最后一个数,长方形的长等于这一列数最后一个数与倒数第二个数的和,那么求这一列数的平方和就相当于求长方形的面积,所以图中所求图形面积分别为$1^2 + 2^2 + 3^2 = 3 × 5 - 1$,$1^2 + 2^2 + 3^2 + 5^2 = 5 × 8 - 1$,$1^2 + 2^2 + 3^2 + 5^2 + 8^2 + 13^2 = 13 × 21 - 1$。观察这组数1,1,2,3,5,8,13······可发现,后一个数是前两个数的和,由此可知,这组数继续往后写为1,1,2,3,5,8,13,21······$21 × (13 + 21) - 1 = 713$,即$1^2 + 2^2 + 3^2 + 5^2 + 8^2 + 13^2 + 21^2 = 21 × 34 - 1$,所以序号为⑦。
解析:
(1)3 5;5 8;13 21
(2)⑦
(2)⑦
2. A、B、C、D、E 五位运动员参加羽毛球循环赛,每两位之间都比一场,每场比赛规定胜者得 2 分,负者得 0 分,已知比赛结果如下:
(1)A 与 B 并列第一名。
(2)C 是第二名。
(3)D 与 E 并列第三名。
求 C 的得分。
(1)A 与 B 并列第一名。
(2)C 是第二名。
(3)D 与 E 并列第三名。
求 C 的得分。
答案:2.C得了4分。 解析:根据题意可知,比赛的场数共为$5 × (5 - 1) ÷ 2 = 10$(场),由于A、B并列第一名,所以A、B不可能都赢4场,最多赢3场;D、E并列第三名,所以D、E不可能都输4场,至少赢1场。根据名次可知,5人得了3种不同的分数,可以确定10场比赛A、B各赢了3场,C赢了2场,D、E各赢了1场,则C得了4分。
解析:
比赛总场数:$5×(5-1)÷2=10$场,总分为$10×2=20$分。
A、B并列第一,最多各赢3场(若赢4场则需胜其他4人,A、B间比赛必有一负,矛盾),各得$3×2=6$分,共$6×2=12$分。
D、E并列第三,至少各赢1场(若赢0场则全负,得分相同但名次应在最后,与C是第二名矛盾),各得$1×2=2$分,共$2×2=4$分。
C的得分为$20-12-4=4$分。
C的得分是$4$分。
A、B并列第一,最多各赢3场(若赢4场则需胜其他4人,A、B间比赛必有一负,矛盾),各得$3×2=6$分,共$6×2=12$分。
D、E并列第三,至少各赢1场(若赢0场则全负,得分相同但名次应在最后,与C是第二名矛盾),各得$1×2=2$分,共$2×2=4$分。
C的得分为$20-12-4=4$分。
C的得分是$4$分。
3. 有 9 个大小、颜色都相同的玻璃球,其中有一个次品比其他正品的质量轻些。用一台天平(不用砝码),至少要称(
2
)次就可以把次品挑出来。答案:3.2 解析:第一次:在天平两端各放3个玻璃球,若平衡,则次品在剩下的3个玻璃球中;若不平衡,则轻的一端的3个玻璃球中有次品。第二次:从含有次品的3个玻璃球中取2个分别放在天平两端,若平衡,则剩下的玻璃球是次品;若不平衡,则轻的一端是次品。
4. 从下面 5 组积木中选取 3 组积木可以拼成下面的正方体,正确的是(
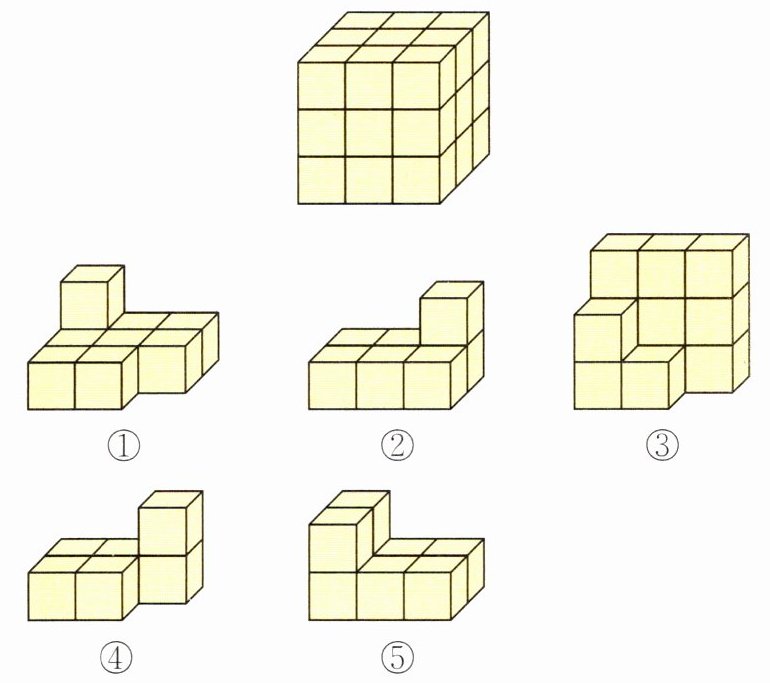
A.①②③
B.①③④
C.②③⑤
D.③④⑤
B
)。
A.①②③
B.①③④
C.②③⑤
D.③④⑤
答案:4.B