7. 新趋势 学科融合 《三国志》中《魏书》的卷数是其他两书之和的$\frac{6}{7},$《蜀书》的卷数是其他两书之和的$\frac{3}{10},$已知《吴书》有20卷,《三国志》全书共有(
65
)卷。答案:7. 65
解析:
设《三国志》全书共有$x$卷。
《魏书》的卷数是其他两书之和的$\frac{6}{7}$,则《魏书》卷数为$\frac{6}{6 + 7}x=\frac{6}{13}x$。
《蜀书》的卷数是其他两书之和的$\frac{3}{10}$,则《蜀书》卷数为$\frac{3}{3 + 10}x=\frac{3}{13}x$。
《吴书》卷数为$x-\frac{6}{13}x-\frac{3}{13}x=\frac{4}{13}x$。
已知《吴书》有20卷,$\frac{4}{13}x = 20$,解得$x=65$。
65
《魏书》的卷数是其他两书之和的$\frac{6}{7}$,则《魏书》卷数为$\frac{6}{6 + 7}x=\frac{6}{13}x$。
《蜀书》的卷数是其他两书之和的$\frac{3}{10}$,则《蜀书》卷数为$\frac{3}{3 + 10}x=\frac{3}{13}x$。
《吴书》卷数为$x-\frac{6}{13}x-\frac{3}{13}x=\frac{4}{13}x$。
已知《吴书》有20卷,$\frac{4}{13}x = 20$,解得$x=65$。
65
8. 笼子里有鸡和兔,一共有26条腿,后来又往笼子里放进(
3
)只兔,并抓出同样只数的鸡,这时笼子里的鸡和兔共有32条腿。答案:8. 3
解析:
设放进的兔和抓出的鸡的只数都为$x$。每放进1只兔增加4条腿,每抓出1只鸡减少2条腿,实际每操作1只净增$4 - 2=2$条腿。根据腿数变化可列方程:$2x=32 - 26$,解得$x=3$。
3
3
9. 大、小两袋糖的质量之比是4:1,从大袋中拿出130克糖放入小袋,这时大、小两袋糖的质量比是7:5。这两袋糖一共重(
600
)克。答案:9. 600
解析:
设两袋糖一共重$x$克。
大袋糖原来的质量为$\frac{4}{4 + 1}x=\frac{4}{5}x$克,小袋糖原来的质量为$\frac{1}{4 + 1}x=\frac{1}{5}x$克。
从大袋拿出130克放入小袋后,大袋糖的质量为$(\frac{4}{5}x - 130)$克,小袋糖的质量为$(\frac{1}{5}x + 130)$克。
根据此时质量比为$7:5$,可得$\frac{\frac{4}{5}x - 130}{\frac{1}{5}x + 130}=\frac{7}{5}$
交叉相乘得:$5(\frac{4}{5}x - 130)=7(\frac{1}{5}x + 130)$
化简:$4x - 650=\frac{7}{5}x + 910$
移项:$4x-\frac{7}{5}x=910 + 650$
$\frac{20}{5}x-\frac{7}{5}x=1560$
$\frac{13}{5}x=1560$
解得$x = 1560×\frac{5}{13}=600$
600
大袋糖原来的质量为$\frac{4}{4 + 1}x=\frac{4}{5}x$克,小袋糖原来的质量为$\frac{1}{4 + 1}x=\frac{1}{5}x$克。
从大袋拿出130克放入小袋后,大袋糖的质量为$(\frac{4}{5}x - 130)$克,小袋糖的质量为$(\frac{1}{5}x + 130)$克。
根据此时质量比为$7:5$,可得$\frac{\frac{4}{5}x - 130}{\frac{1}{5}x + 130}=\frac{7}{5}$
交叉相乘得:$5(\frac{4}{5}x - 130)=7(\frac{1}{5}x + 130)$
化简:$4x - 650=\frac{7}{5}x + 910$
移项:$4x-\frac{7}{5}x=910 + 650$
$\frac{20}{5}x-\frac{7}{5}x=1560$
$\frac{13}{5}x=1560$
解得$x = 1560×\frac{5}{13}=600$
600
10. (2025·苏州吴江区期末)2025年是新中国成立76周年,实验小学举行了以“礼赞新中国,放歌新时代”为主题的歌咏比赛。比赛分单人独唱和双人合唱,共有18组,30名学生参加比赛,单人独唱有(
6
)组,双人合唱有(12
)组。答案:10. 6 12
解析:
设单人独唱有$x$组,双人合唱有$y$组。
根据题意可得方程组:
$\begin{cases}x + y = 18 \\ x + 2y = 30\end{cases}$
用第二个方程减去第一个方程得:$x + 2y - (x + y) = 30 - 18$,即$y = 12$
将$y = 12$代入$x + y = 18$,得$x = 18 - 12 = 6$
单人独唱有$6$组,双人合唱有$12$组。
根据题意可得方程组:
$\begin{cases}x + y = 18 \\ x + 2y = 30\end{cases}$
用第二个方程减去第一个方程得:$x + 2y - (x + y) = 30 - 18$,即$y = 12$
将$y = 12$代入$x + y = 18$,得$x = 18 - 12 = 6$
单人独唱有$6$组,双人合唱有$12$组。
11. 夏阳(男)和苏文(女)是学校围棋社的社员。夏阳说:“除了我,男、女生的人数比是1:2。”苏文说:“除了我,男、女生的人数比是2:3。”围棋社有男生(
6
)人,女生(10
)人。答案:11. 6 10 解析:除夏阳之外的社员人数与除苏文之外的社员人数是相等的,可看作单位“1”,除夏阳之外的男生人数占单位“1”的$\frac{1}{1+2}$,总的男生人数占单位“1”的$\frac{2}{2+3}$,这两个分数的差对应的就是夏阳这1人,因此单位“1”是1÷($\frac{2}{2+3}$ - $\frac{1}{1+2}$)=15(人),那么男生人数是15×$\frac{2}{2+3}$=6(人),女生人数是15+1 - 6=10(人)。
解析:
设除夏阳之外的社员人数为单位“1”。
除夏阳之外男、女生人数比是1:2,所以除夏阳之外男生人数占单位“1”的$\frac{1}{1+2}=\frac{1}{3}$。
除苏文之外男、女生人数比是2:3,此时总人数仍为单位“1”(因为除夏阳和除苏文的社员人数相等),所以此时男生人数占单位“1”的$\frac{2}{2+3}=\frac{2}{5}$。
这两个男生占比的差对应夏阳1人,故单位“1”的人数为:$1÷(\frac{2}{5}-\frac{1}{3})=1÷(\frac{6}{15}-\frac{5}{15})=1÷\frac{1}{15}=15$(人)。
男生人数为:$15×\frac{2}{5}=6$(人)。
总人数为:$15 + 1 = 16$(人)(加上夏阳)。
女生人数为:$16 - 6 = 10$(人)。
6;10
除夏阳之外男、女生人数比是1:2,所以除夏阳之外男生人数占单位“1”的$\frac{1}{1+2}=\frac{1}{3}$。
除苏文之外男、女生人数比是2:3,此时总人数仍为单位“1”(因为除夏阳和除苏文的社员人数相等),所以此时男生人数占单位“1”的$\frac{2}{2+3}=\frac{2}{5}$。
这两个男生占比的差对应夏阳1人,故单位“1”的人数为:$1÷(\frac{2}{5}-\frac{1}{3})=1÷(\frac{6}{15}-\frac{5}{15})=1÷\frac{1}{15}=15$(人)。
男生人数为:$15×\frac{2}{5}=6$(人)。
总人数为:$15 + 1 = 16$(人)(加上夏阳)。
女生人数为:$16 - 6 = 10$(人)。
6;10
1.

求已经看了多少页,小妍在做这一题时想到以下四种方法:
$①48÷4×3 ②48×\frac{3}{4} ③48÷\frac{3}{4} ④48×\frac{7}{4}−48$
在这些方法中,正确的有(
A.1
B.2
C.3
D.4

求已经看了多少页,小妍在做这一题时想到以下四种方法:
$①48÷4×3 ②48×\frac{3}{4} ③48÷\frac{3}{4} ④48×\frac{7}{4}−48$
在这些方法中,正确的有(
C
)种。A.1
B.2
C.3
D.4
答案:1. C
2. 某班女生人数是男生人数的$\frac{4}{5},$下列推断错误的是(
A.男生人数比女生人数多$\frac{1}{4}$
B.男生人数与女生人数的比是5:4
C.女生人数比男生人数少$\frac{1}{4}$
D.女生人数与全班人数的比是4:9
C
)。A.男生人数比女生人数多$\frac{1}{4}$
B.男生人数与女生人数的比是5:4
C.女生人数比男生人数少$\frac{1}{4}$
D.女生人数与全班人数的比是4:9
答案:2. C
解析:
设男生人数为$5x$,则女生人数为$4x$。
A. 男生人数比女生人数多$\frac{5x - 4x}{4x} = \frac{1}{4}$,正确。
B. 男生人数与女生人数的比是$5x:4x = 5:4$,正确。
C. 女生人数比男生人数少$\frac{5x - 4x}{5x} = \frac{1}{5}$,错误。
D. 女生人数与全班人数的比是$4x:(5x + 4x) = 4:9$,正确。
C
A. 男生人数比女生人数多$\frac{5x - 4x}{4x} = \frac{1}{4}$,正确。
B. 男生人数与女生人数的比是$5x:4x = 5:4$,正确。
C. 女生人数比男生人数少$\frac{5x - 4x}{5x} = \frac{1}{5}$,错误。
D. 女生人数与全班人数的比是$4x:(5x + 4x) = 4:9$,正确。
C
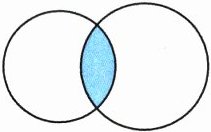
3. 如图,两个圆重叠,重叠部分的面积是大圆面积的$\frac{1}{8},$是小圆面积的$\frac{1}{5},$那么小圆面积是大圆面积的(
A.$\frac{5}{8}$
B.$\frac{8}{5}$
C.$\frac{3}{8}$
D.$ \frac{3}{5}$
A
)。
A.$\frac{5}{8}$
B.$\frac{8}{5}$
C.$\frac{3}{8}$
D.$ \frac{3}{5}$
答案:3. A
解析:
设重叠部分面积为$S$。
因为重叠部分面积是大圆面积的$\frac{1}{8}$,所以大圆面积为$8S$。
又因为重叠部分面积是小圆面积的$\frac{1}{5}$,所以小圆面积为$5S$。
则小圆面积与大圆面积的比为$\frac{5S}{8S}=\frac{5}{8}$。
A
因为重叠部分面积是大圆面积的$\frac{1}{8}$,所以大圆面积为$8S$。
又因为重叠部分面积是小圆面积的$\frac{1}{5}$,所以小圆面积为$5S$。
则小圆面积与大圆面积的比为$\frac{5S}{8S}=\frac{5}{8}$。
A
4. 2025年第九届亚洲冬季运动会的吉祥物“滨滨”和“妮妮”自亮相以来,深受人们喜爱。某纪念品商店购入一批吉祥物玩偶,已经售卖了全部的65%,还剩下140个玩偶,该纪念品商店共购入多少个吉祥物玩偶?列式正确的是(
A.140×(1−65%)
B.140÷(1−65%)
C.140÷65%
D.140÷(1+65%)
B
)。A.140×(1−65%)
B.140÷(1−65%)
C.140÷65%
D.140÷(1+65%)
答案:4. B