4. 如图,一顶圆锥形帐篷的底面半径$BC$是1.25米,平平测得它的影子$CD$是1.25米,同时又测得一根竹竿的长度是0.8米,影长是1米。这顶帐篷高多少米?(5分)
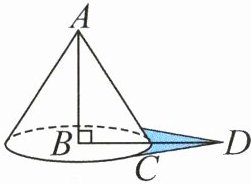

答案:4. 解:设这顶帐篷高x米。
$\frac{0.8}{1}=\frac{x}{1.25 + 1.25}$,x = 2
答:这顶帐篷高2米。
$\frac{0.8}{1}=\frac{x}{1.25 + 1.25}$,x = 2
答:这顶帐篷高2米。
5. 俄罗斯古代难题:一个雇工每年的工资是12卢布加1件长袍,工作7个月以后,他准备离开,雇主付给他1件长袍和5卢布。这件长袍的价格是多少卢布?(5分)
答案:5. 解:设这件长袍的价格是x卢布。
(12 + x):12 = (5 + x):7,x = 4.8
答:这件长袍的价格是4.8卢布。
(12 + x):12 = (5 + x):7,x = 4.8
答:这件长袍的价格是4.8卢布。
1. 师徒两人加工一批零件,师父每小时加工40个,徒弟每小时加工30个。师父先加工了这批零件的一半后,剩下的由徒弟去加工,两人共用3.5小时完成了这批零件的加工任务。这批零件共有(
120
)个。(4分)答案:1. 120 解析:根据题意可知,师徒两人加工的零件个数相同,则他们每小时加工的零件个数与加工的时间成反比例。师徒两人每小时加工的零件个数之比是40:30 = 4:3,则加工的时间之比是3:4,则师父加工零件用了3.5×$\frac{3}{4 + 3}$ = 1.5(时),这批零件共有40×1.5×2 = 120(个)。
解析:
师徒每小时加工零件个数比为$40:30 = 4:3$,因加工零件数相同,时间比与效率比成反比,即时间比为$3:4$。
总时间为$3.5$小时,师父加工时间为$3.5×\frac{3}{3 + 4}=1.5$小时。
师父加工零件数为$40×1.5 = 60$个,这批零件共有$60×2 = 120$个。
120
总时间为$3.5$小时,师父加工时间为$3.5×\frac{3}{3 + 4}=1.5$小时。
师父加工零件数为$40×1.5 = 60$个,这批零件共有$60×2 = 120$个。
120
2. 甲、乙两车分别从$A$、$B$两地同时相对开出,当甲车行至全程的$\dfrac{4}{7}$时,乙车已行的路程与剩下的路程的比是$4:5$;当甲车到达$B$地时,乙车离$A$地还有16千米。$A$、$B$两地相距多少千米?(6分)
答案:2. $\frac{4}{7}:\frac{4}{4 + 5}=9:7$ 解:设A、B两地相距x千米。
$\frac{x}{x - 16}=\frac{9}{7}$,x = 72
答:A、B两地相距72千米。 解析:当甲车行了全程的$\frac{4}{7}$时,乙车行了全程的$\frac{4}{4 + 5}=\frac{4}{9}$,甲、乙两车的速度比为$\frac{4}{7}:\frac{4}{9}=9:7$,当甲车到达B地时,两车的路程比为9:7,然后设未知数列比例式解答。
$\frac{x}{x - 16}=\frac{9}{7}$,x = 72
答:A、B两地相距72千米。 解析:当甲车行了全程的$\frac{4}{7}$时,乙车行了全程的$\frac{4}{4 + 5}=\frac{4}{9}$,甲、乙两车的速度比为$\frac{4}{7}:\frac{4}{9}=9:7$,当甲车到达B地时,两车的路程比为9:7,然后设未知数列比例式解答。