6. 新趋势图表信息 为贯彻落实“双减”政策,了解我市小学生的校外作业负担情况,某教育部门通过网络平台随机抽取了部分小学三至六年级的学生,并对他们完成校外作业时间进行了问卷调查,统计结果如下:
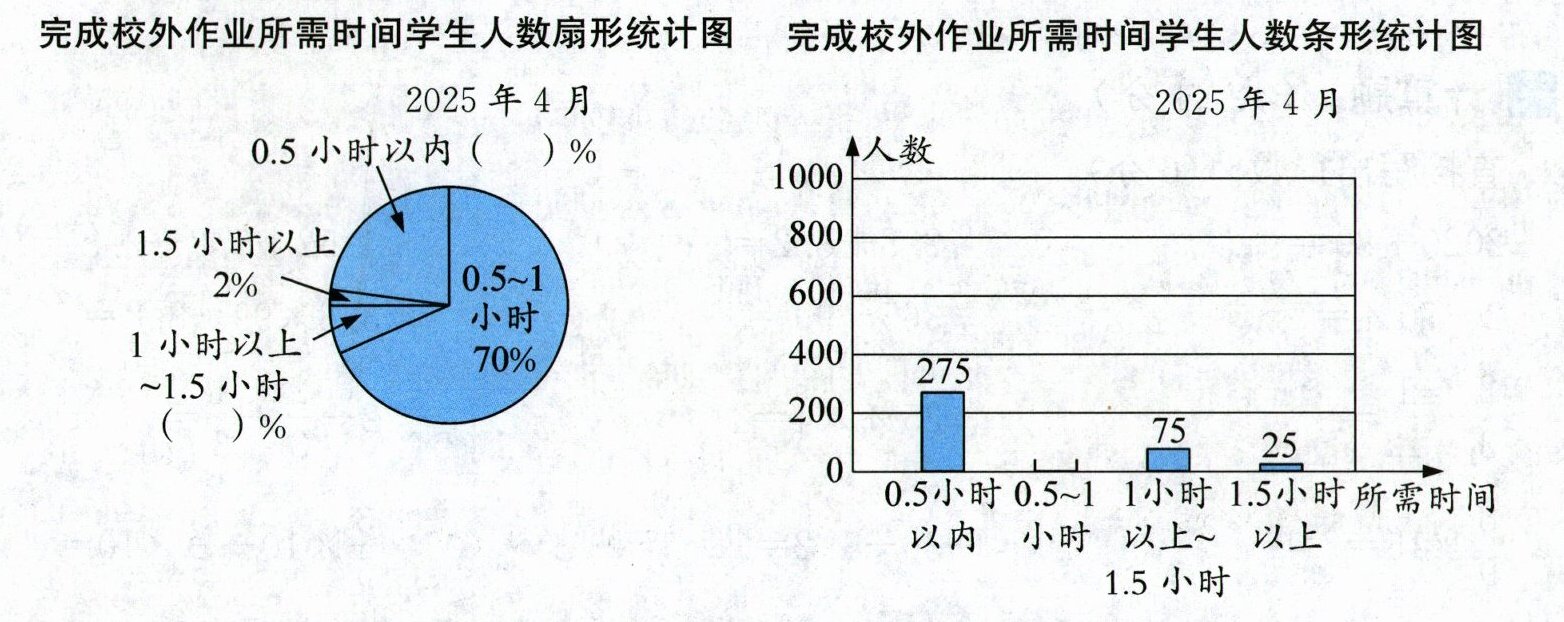
(1) 根据这两幅不完整的统计图,计算出参加问卷调查的总人数。(2分)
(2) 根据信息,把两幅统计图补充完整。(2分)
(3) 按教育部规定,小学中、高年级(三至六年级)学生校外作业时间不得超过1小时。根据统计结果,估计一下我市60000名小学中、高年级学生中大约有多少人达到了此项要求。(3分)

(1) 根据这两幅不完整的统计图,计算出参加问卷调查的总人数。(2分)
(2) 根据信息,把两幅统计图补充完整。(2分)
(3) 按教育部规定,小学中、高年级(三至六年级)学生校外作业时间不得超过1小时。根据统计结果,估计一下我市60000名小学中、高年级学生中大约有多少人达到了此项要求。(3分)
答案:6. (1)25÷2% = 1250(人) (2)扇形统计图略,从上往下填:22 6,条形统计图略,所需时间在0.5~1小时的有875人。
(3)60000×(22% + 70%) = 55200(人)
(3)60000×(22% + 70%) = 55200(人)
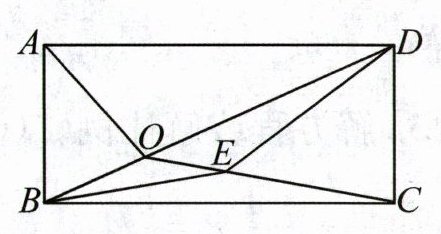
1. 如图,在长方形ABCD中,BD是一条对角线,点O在BD上,三角形ABO的面积是5平方厘米,三角形DEO的面积与三角形DEC的面积比是1:2。三角形ABO的面积比三角形BEO的面积大(
$\frac{10}{3}$
)平方厘米。(4分)
答案:1. $\frac{10}{3}$ 解析:S_三角形ABO + S_三角形AOD = $\frac{1}{2}$S_长方形ABCD,S_三角形AOD + S_三角形BOC = $\frac{1}{2}$S_长方形ABCD,则S_三角形ABO = S_三角形BOC。
因为S_三角形DEO:S_三角形DEC = 1:2,且三角形DEO和三角形DEC等高,所以OE:EC = 1:2,则S_三角形BEO:S_三角形BEC = 1:2,又因为S_三角形BEO + S_三角形BEC = S_三角形BOC = S_三角形ABO = 5平方厘米,所以S_三角形BEO = 5×$\frac{1}{1 + 2}$ = $\frac{5}{3}$(平方厘米),所以S_三角形ABO - S_三角形BEO = 5 - $\frac{5}{3}$ = $\frac{10}{3}$(平方厘米)。
因为S_三角形DEO:S_三角形DEC = 1:2,且三角形DEO和三角形DEC等高,所以OE:EC = 1:2,则S_三角形BEO:S_三角形BEC = 1:2,又因为S_三角形BEO + S_三角形BEC = S_三角形BOC = S_三角形ABO = 5平方厘米,所以S_三角形BEO = 5×$\frac{1}{1 + 2}$ = $\frac{5}{3}$(平方厘米),所以S_三角形ABO - S_三角形BEO = 5 - $\frac{5}{3}$ = $\frac{10}{3}$(平方厘米)。
2. 某校六年级学生共有152人,选出男生的$\frac{1}{11}$和5个女生参加科技小组,剩下的男、女生人数相等。六年级男、女生各有多少人?(6分)
答案:
2. (152 - 5)÷(11 + 10) = 7(人) 男生:7×11 = 77(人) 女生:7×10 + 5 = 75(人) 解析:画图分析:
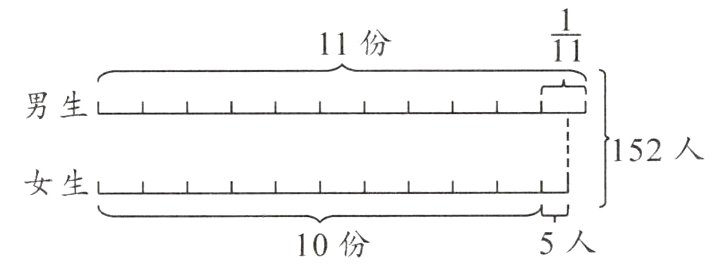
从图中可知,男生有11份,女生有10份多5人,且男、女生共有152人,可求出1份有(152 - 5)÷(11 + 10) = 7(人),再分别求出男、女生人数。
2. (152 - 5)÷(11 + 10) = 7(人) 男生:7×11 = 77(人) 女生:7×10 + 5 = 75(人) 解析:画图分析:

从图中可知,男生有11份,女生有10份多5人,且男、女生共有152人,可求出1份有(152 - 5)÷(11 + 10) = 7(人),再分别求出男、女生人数。