类型 数形结合巧解题
例 如图,东西、南北两条路交叉成直角,甲在路口中心正南方向 1500 米处,乙在路口中心。甲由南向北,乙由西向东,同时出发。5 分钟后,甲还没走到路口,两人离路口中心的距离相等;又走了 45 分钟后,两人离路口中心的距离再次相等。甲、乙两人每分钟各行多少米?

例 如图,东西、南北两条路交叉成直角,甲在路口中心正南方向 1500 米处,乙在路口中心。甲由南向北,乙由西向东,同时出发。5 分钟后,甲还没走到路口,两人离路口中心的距离相等;又走了 45 分钟后,两人离路口中心的距离再次相等。甲、乙两人每分钟各行多少米?

答案:
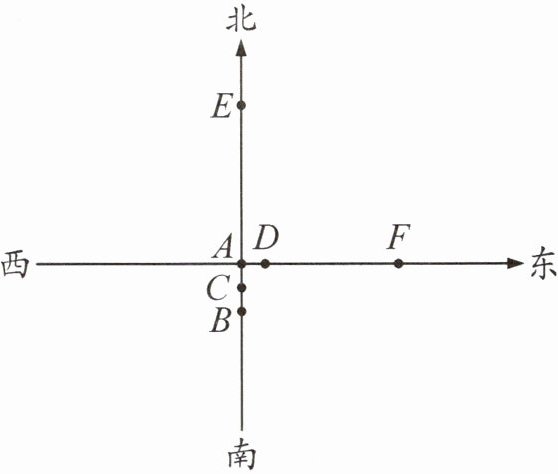
思路分析 如图,5 分钟后,甲从 B 走到 C,乙从 A 走到 D,即 $ AC = AD $,所以甲、乙 5 分钟共行了 AB 段的距离,即 1500 米,这时可求出甲、乙的速度和为 $ 1500 ÷ 5 = 300 $(米/分)。再走 45 分钟后,甲走到 E,乙走到 F,此时 $ AE = AF $,所以甲 50 分钟行 BE 段的距离,比乙 50 分钟多行 AB 段的距离,即 1500 米,这时可求出甲、乙的速度差为 $ 1500 ÷ (5 + 45) = 30 $(米/分),再根据和差问题的数量关系可求出甲、乙的速度。
规范解答 $ 1500 ÷ 5 = 300 $(米/分)
$ 1500 ÷ (5 + 45) = 30 $(米/分) 甲:$ (300 + 30) ÷ 2 = 165 $(米/分) 乙:$ 300 - 165 = 135 $(米/分) 答:甲每分钟行 165 米,乙每分钟行 135 米。
思路分析 如图,5 分钟后,甲从 B 走到 C,乙从 A 走到 D,即 $ AC = AD $,所以甲、乙 5 分钟共行了 AB 段的距离,即 1500 米,这时可求出甲、乙的速度和为 $ 1500 ÷ 5 = 300 $(米/分)。再走 45 分钟后,甲走到 E,乙走到 F,此时 $ AE = AF $,所以甲 50 分钟行 BE 段的距离,比乙 50 分钟多行 AB 段的距离,即 1500 米,这时可求出甲、乙的速度差为 $ 1500 ÷ (5 + 45) = 30 $(米/分),再根据和差问题的数量关系可求出甲、乙的速度。

规范解答 $ 1500 ÷ 5 = 300 $(米/分)
$ 1500 ÷ (5 + 45) = 30 $(米/分) 甲:$ (300 + 30) ÷ 2 = 165 $(米/分) 乙:$ 300 - 165 = 135 $(米/分) 答:甲每分钟行 165 米,乙每分钟行 135 米。
跟踪练习 甲、乙两人分别在一个十字路口的正北方向和正东方向,两人距离十字路口的距离之和是 500 米。若两人都向十字路口走去,则 4 分钟后两人刚好在十字路口相遇;若甲由北向南,乙由西向东走,则 20 分钟后两人离十字路口的距离相等且甲在十字路口南侧。甲、乙两人的速度分别是多少米/分?
答案:
思维创新探究
[跟踪练习] $500 ÷ 4 = 125$(米/分)
$500 ÷ 20 = 25$(米/分)
甲:$(125 + 25) ÷ 2 = 75$(米/分)
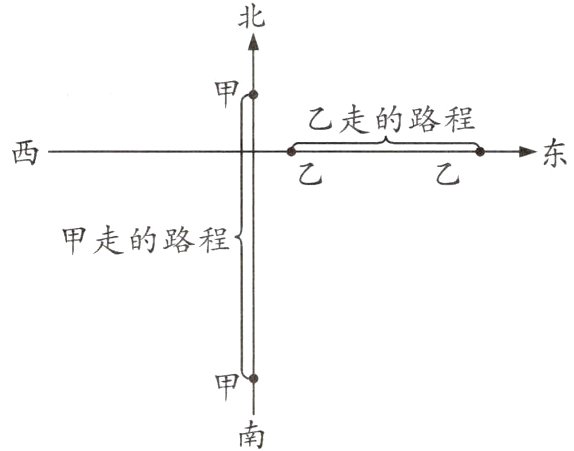
乙:$(125 - 25) ÷ 2 = 50$(米/分) 解析 两人都向十字路口走,可看成是相遇问题,根据相遇时间可求出两人的速度和。甲由北向南、乙由西向东走,两人离十字路口的距离相等,如图,在相同的时间内,甲比乙多走$500$米,从而可求出甲比乙每分钟多走多少米,即两人的速度差。已知两人的速度和与速度差,用和差公式求解即可。
思维创新探究
[跟踪练习] $500 ÷ 4 = 125$(米/分)
$500 ÷ 20 = 25$(米/分)
甲:$(125 + 25) ÷ 2 = 75$(米/分)
乙:$(125 - 25) ÷ 2 = 50$(米/分) 解析 两人都向十字路口走,可看成是相遇问题,根据相遇时间可求出两人的速度和。甲由北向南、乙由西向东走,两人离十字路口的距离相等,如图,在相同的时间内,甲比乙多走$500$米,从而可求出甲比乙每分钟多走多少米,即两人的速度差。已知两人的速度和与速度差,用和差公式求解即可。
