例1 一辆汽车从甲地开往乙地,每小时行驶40千米,返回时每小时行驶50千米,结果返回时比去时少用48分钟。求甲、乙两地之间的路程。
答案:规范解答 去时速度:返回速度=40:50=4:5 去时时间:返回时间=5:4 去时时间:48÷(5−4)×5=240(分) 240分=4时 甲、乙两地之间的路程:40×4=160(千米) 答:甲、乙两地之间的路程是160千米。
跟踪练习1 (2025·泰州海陵区期末改编)在自行车早期发展过程中出现过一种高轮自行车(如图)。前轮和后轮的直径比是()。骑行时,同一时间内前轮和后轮行驶的路程相等,如果前轮比后轮少转动55次,那么后轮转动()次。
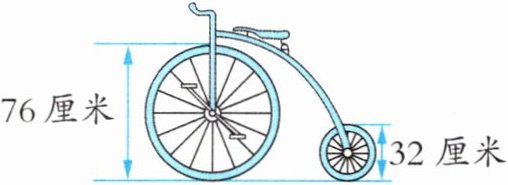

答案:1. 首先求前轮和后轮的直径比:
已知前轮直径$d_1 = 76$厘米,后轮直径$d_2 = 32$厘米。
根据比的定义,$d_1:d_2=76:32$,化简$\frac{76}{32}=\frac{19}{8}$,即$19:8$。
2. 然后根据圆的周长公式$C = \pi d$($C$表示周长,$d$表示直径):
设后轮转动$x$次,因为同一时间内前轮和后轮行驶的路程相等,前轮转动$(x - 55)$次。
由$C_1× n_1=C_2× n_2$($C_1$、$C_2$分别为前轮、后轮周长,$n_1$、$n_2$分别为前轮、后轮转动次数),$C=\pi d$,可得$\pi d_1×(x - 55)=\pi d_2× x$。
两边同时约去$\pi$,把$d_1 = 76$,$d_2 = 32$代入得:$76×(x - 55)=32x$。
展开括号:$76x-76×55 = 32x$。
移项:$76x-32x=76×55$。
合并同类项:$(76 - 32)x=76×55$,即$44x=76×55$。
求解$x$:$x=\frac{76×55}{44}$。
计算$\frac{76×55}{44}=\frac{76×5}{4}=\frac{380}{4}=95$。
所以前轮和后轮的直径比是$19:8$,后轮转动$95$次。
故答案依次为:$19:8$;$95$。
已知前轮直径$d_1 = 76$厘米,后轮直径$d_2 = 32$厘米。
根据比的定义,$d_1:d_2=76:32$,化简$\frac{76}{32}=\frac{19}{8}$,即$19:8$。
2. 然后根据圆的周长公式$C = \pi d$($C$表示周长,$d$表示直径):
设后轮转动$x$次,因为同一时间内前轮和后轮行驶的路程相等,前轮转动$(x - 55)$次。
由$C_1× n_1=C_2× n_2$($C_1$、$C_2$分别为前轮、后轮周长,$n_1$、$n_2$分别为前轮、后轮转动次数),$C=\pi d$,可得$\pi d_1×(x - 55)=\pi d_2× x$。
两边同时约去$\pi$,把$d_1 = 76$,$d_2 = 32$代入得:$76×(x - 55)=32x$。
展开括号:$76x-76×55 = 32x$。
移项:$76x-32x=76×55$。
合并同类项:$(76 - 32)x=76×55$,即$44x=76×55$。
求解$x$:$x=\frac{76×55}{44}$。
计算$\frac{76×55}{44}=\frac{76×5}{4}=\frac{380}{4}=95$。
所以前轮和后轮的直径比是$19:8$,后轮转动$95$次。
故答案依次为:$19:8$;$95$。
例2 如图,在杠杆左侧刻度2处挂了3个质量均为10克的砝码,在右侧刻度5处挂了1个质量为12克的砝码,此时杠杆平衡。如果左侧拿走一个砝码,那么左侧剩下的砝码应移到左侧刻度()处,才能使杠杆仍然保持平衡。
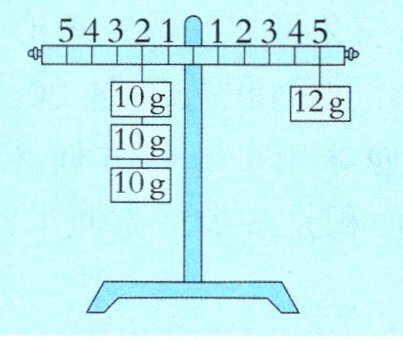

答案:思路分析 首先找变量,确定哪两个量是相关的量。在这道题中,砝码的总质量和砝码到支点的距离是两个相关联的量;然后分析这两个相关联的量之间是什么关系。由题意可知,左侧砝码的总质量×左侧砝码到支点的距离=右侧砝码的总质量×右侧砝码到支点的距离,即(10×3)×2=12×5,它们的乘积一定,此时杠杆平衡。根据题意,右侧没变,左侧拿走一个砝码,左侧砝码的总质量变为10×2=20(克),要使杠杆平衡,应考虑20×()=12×5,从而求出左侧剩下的砝码到支点的距离为12×5÷20=3,所以左侧剩下的砝码应移动到左侧刻度3处,才能使杠杆仍然保持平衡。
规范解答 3
规范解答 3