1. 一组对边
平行
,另一组对边不平行
的四边形叫作梯形,其中互相平行的一组对边中,较短的边叫作梯形的上底
,较长的边叫作梯形的下底
,另外两条边叫作梯形的腰
。答案:1. 平行 不平行 上底 下底 腰
2. 两腰
相等
的梯形叫作等腰梯形。答案:2. 相等
3. 有一个角是
直角
的梯形叫作直角梯形。答案:3. 直角
1. 如图,在梯形 $ABCD$ 中,$∠ B = 115^{\circ}$,则 $∠ C$ 的大小是(
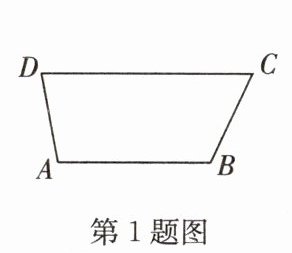
A.$50^{\circ}$
B.$65^{\circ}$
C.$75^{\circ}$
D.$85^{\circ}$
B
)
A.$50^{\circ}$
B.$65^{\circ}$
C.$75^{\circ}$
D.$85^{\circ}$
答案:1. B
解析:
证明:在梯形$ABCD$中,$AB// CD$,
$\because AB// CD$,
$\therefore ∠ B+∠ C=180^{\circ}$(两直线平行,同旁内角互补),
$\because ∠ B = 115^{\circ}$,
$\therefore ∠ C=180^{\circ}-∠ B=180^{\circ}-115^{\circ}=65^{\circ}$。
B
$\because AB// CD$,
$\therefore ∠ B+∠ C=180^{\circ}$(两直线平行,同旁内角互补),
$\because ∠ B = 115^{\circ}$,
$\therefore ∠ C=180^{\circ}-∠ B=180^{\circ}-115^{\circ}=65^{\circ}$。
B
2. 如图,在四边形 $ABCD$ 中,$AD// BC$,$∠ ABC = 90^{\circ}$,$AB = 3$,$AD = 2$,若 $∠ C = 45^{\circ}$,则 $BC$ 的长为(
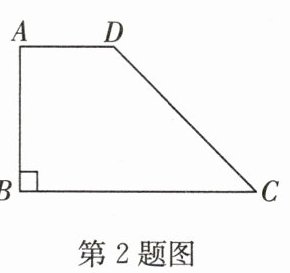
A.$6$
B.$4$
C.$2 + 3\sqrt{2}$
D.$5$
D
)
A.$6$
B.$4$
C.$2 + 3\sqrt{2}$
D.$5$
答案:2. D
解析:
解:过点$D$作$DE ⊥ BC$于点$E$。
因为$AD // BC$,$∠ ABC = 90^{\circ}$,$DE ⊥ BC$,所以四边形$ABED$是矩形。
所以$BE = AD = 2$,$DE = AB = 3$。
在$Rt△ DEC$中,$∠ C = 45^{\circ}$,所以$EC = DE = 3$。
因此$BC = BE + EC = 2 + 3 = 5$。
答案:D
因为$AD // BC$,$∠ ABC = 90^{\circ}$,$DE ⊥ BC$,所以四边形$ABED$是矩形。
所以$BE = AD = 2$,$DE = AB = 3$。
在$Rt△ DEC$中,$∠ C = 45^{\circ}$,所以$EC = DE = 3$。
因此$BC = BE + EC = 2 + 3 = 5$。
答案:D
3. 在梯形 $ABCD$ 中,$AD// BC$,$AB = CD = AD = 2$,$∠ B = 60^{\circ}$,则下底 $BC$ 的长是(
A.$3$
B.$4$
C.$2\sqrt{3}$
D.$2 + 2\sqrt{3}$
B
)A.$3$
B.$4$
C.$2\sqrt{3}$
D.$2 + 2\sqrt{3}$
答案:3. B
解析:
过点$A$作$AE ⊥ BC$于点$E$,过点$D$作$DF ⊥ BC$于点$F$。
因为$AD // BC$,$AE ⊥ BC$,$DF ⊥ BC$,所以四边形$AEFD$是矩形,$EF = AD = 2$。
在梯形$ABCD$中,$AB = CD$,所以梯形$ABCD$是等腰梯形,$∠ B = ∠ C = 60°$。
在$Rt△ ABE$中,$∠ B = 60°$,$AB = 2$,$\cos 60° = \frac{BE}{AB}$,则$BE = AB · \cos 60° = 2 × \frac{1}{2} = 1$。
同理,$CF = 1$。
所以$BC = BE + EF + CF = 1 + 2 + 1 = 4$。
B
因为$AD // BC$,$AE ⊥ BC$,$DF ⊥ BC$,所以四边形$AEFD$是矩形,$EF = AD = 2$。
在梯形$ABCD$中,$AB = CD$,所以梯形$ABCD$是等腰梯形,$∠ B = ∠ C = 60°$。
在$Rt△ ABE$中,$∠ B = 60°$,$AB = 2$,$\cos 60° = \frac{BE}{AB}$,则$BE = AB · \cos 60° = 2 × \frac{1}{2} = 1$。
同理,$CF = 1$。
所以$BC = BE + EF + CF = 1 + 2 + 1 = 4$。
B
4. 如图,在梯形 $ABCD$ 中,$AB// DC$,$DE// CB$,若 $CD = 4$,$△ ADE$ 的周长为 $18$,则梯形 $ABCD$ 的周长为(
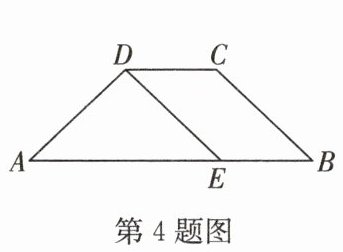
A.$22$
B.$26$
C.$38$
D.$30$
B
)
A.$22$
B.$26$
C.$38$
D.$30$
答案:4. B
解析:
证明:
∵ $AB // DC$,$DE // CB$,
∴ 四边形 $DEBC$ 是平行四边形,
∴ $DE = CB$,$EB = CD = 4$。
∵ $△ ADE$ 的周长为 $18$,
∴ $AD + DE + AE = 18$。
梯形 $ABCD$ 的周长为:
$AD + DC + CB + AB = AD + CD + DE + (AE + EB)$
$= (AD + DE + AE) + CD + EB$
$= 18 + 4 + 4 = 26$。
答案:B
∵ $AB // DC$,$DE // CB$,
∴ 四边形 $DEBC$ 是平行四边形,
∴ $DE = CB$,$EB = CD = 4$。
∵ $△ ADE$ 的周长为 $18$,
∴ $AD + DE + AE = 18$。
梯形 $ABCD$ 的周长为:
$AD + DC + CB + AB = AD + CD + DE + (AE + EB)$
$= (AD + DE + AE) + CD + EB$
$= 18 + 4 + 4 = 26$。
答案:B
5. 一个梯形的下底比上底多 $2\mathrm{cm}$,高是 $5\mathrm{cm}$,面积为 $40\mathrm{cm}^2$,那么这个梯形的上底长为
7
$\mathrm{cm}$。答案:5. 7
解析:
设梯形的上底长为$x\ \mathrm{cm}$,则下底长为$(x + 2)\ \mathrm{cm}$。
根据梯形面积公式$S=\dfrac{(a + b)h}{2}$(其中$a$、$b$为上、下底,$h$为高),可得:
$\begin{aligned}\dfrac{(x + x + 2)×5}{2}&=40\\\dfrac{(2x + 2)×5}{2}&=40\\(2x + 2)×5&=80\\2x + 2&=16\\2x&=14\\x&=7\end{aligned}$
7
根据梯形面积公式$S=\dfrac{(a + b)h}{2}$(其中$a$、$b$为上、下底,$h$为高),可得:
$\begin{aligned}\dfrac{(x + x + 2)×5}{2}&=40\\\dfrac{(2x + 2)×5}{2}&=40\\(2x + 2)×5&=80\\2x + 2&=16\\2x&=14\\x&=7\end{aligned}$
7
6. 如图,在梯形 $ABCD$ 中,$AD// BC$,$M$ 是 $AD$ 的中点,且 $MB = MC$,若 $AD = 4$,$AB = 6$,$BC = 8$,求梯形 $ABCD$ 的周长。
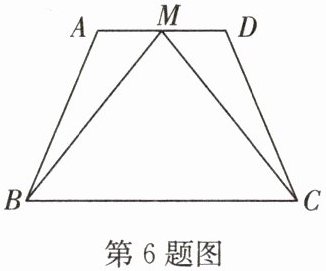

答案:6. 解:
∵AD//BC,
∴∠AMB=∠MBC,∠DMC=∠MCB.
∵MC=MB,
∴∠MBC=∠MCB,
∴∠AMB=∠DMC.
∵M 是 AD 的中点,
∴AM=DM.
在△AMB 和△DMC 中,{ AM = DM, ∠AMB = ∠DMC, MB = MC,
∴△AMB≌△DMC(SAS),
∴DC=AB=6,
∴梯形 ABCD 的周长为 AB+BC+CD+AD=6+8+6+4=24.
∵AD//BC,
∴∠AMB=∠MBC,∠DMC=∠MCB.
∵MC=MB,
∴∠MBC=∠MCB,
∴∠AMB=∠DMC.
∵M 是 AD 的中点,
∴AM=DM.
在△AMB 和△DMC 中,{ AM = DM, ∠AMB = ∠DMC, MB = MC,
∴△AMB≌△DMC(SAS),
∴DC=AB=6,
∴梯形 ABCD 的周长为 AB+BC+CD+AD=6+8+6+4=24.