21.(14分)(2024·秦淮区期末)某校为了丰富学生学习生活，开设城墙文化、英语阅读、篮球三项活动课程以提升学生的素养，学工处随机抽取了部分学生对这三项活动的兴趣情况进行了调查(每人从中只能选一项)，并将调查结果绘制成如图所示的两幅统计图，请结合图中信息解答下列问题：
(1)将条形统计图补充完整；
(2)本次抽样调查的样本容量是
(3)已知该校有1200名学生，请你根据样本估计全校学生中喜欢篮球的人数.
(1)将条形统计图补充完整；
(2)本次抽样调查的样本容量是
100
；(3)已知该校有1200名学生，请你根据样本估计全校学生中喜欢篮球的人数.
答案：
21.(1)解:本次调查的女生有$10÷20\% = 50$(人)，喜欢英语阅读的女生有$50 - 10 - 16 = 24$(人).
补全条形统计图如答图.
喜欢各类活动的学生人数条形统计图
(2)100
(3)解:$1200×\frac{14 + 16}{100} = 360$.
答:估计全校学生中喜欢篮球的人数为360.
21.(1)解:本次调查的女生有$10÷20\% = 50$(人)，喜欢英语阅读的女生有$50 - 10 - 16 = 24$(人).
补全条形统计图如答图.
喜欢各类活动的学生人数条形统计图(2)100
(3)解:$1200×\frac{14 + 16}{100} = 360$.
答:估计全校学生中喜欢篮球的人数为360.
22.(14分)为了增强学生的消防安全意识，某校组织了一次全校2500名学生都参加的“消防安全知识”考试. 阅卷后，学校团委随机抽取了100份考卷进行分析统计，发现考试成绩($x$分)的最低分为51分，最高分为满分100分，并绘制了如下尚不完整的统计图表.
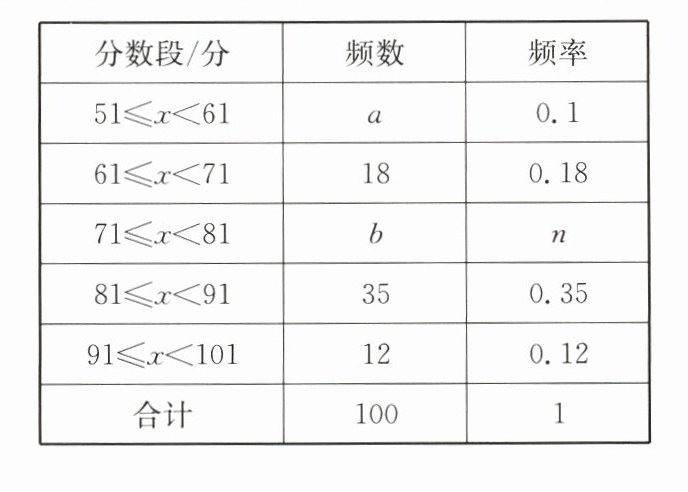
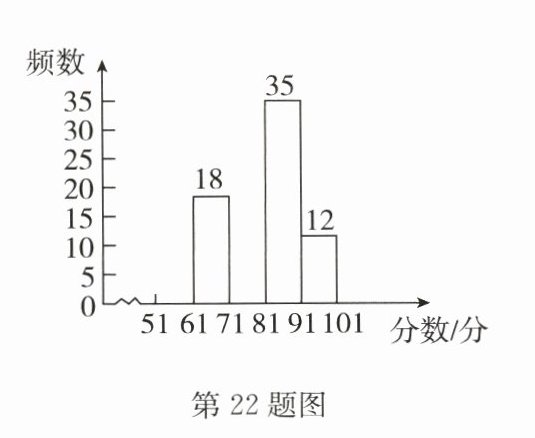
请根据图表提供的信息，解答下列问题：
(1)填空：$a=$
(2)将频数分布直方图补充完整；
(3)该校对考试成绩为$91≤ x≤100$的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1∶3∶6，请你估算全校获得二等奖的学生人数.
请根据图表提供的信息，解答下列问题：
(1)填空：$a=$
10
，$b=$25
，$n=$0.25
；(2)将频数分布直方图补充完整；
(3)该校对考试成绩为$91≤ x≤100$的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1∶3∶6，请你估算全校获得二等奖的学生人数.
答案：
22.(1)10 25 0.25
(2)解:补全频数分布直方图如答图所示.
(3)解:$2500×\frac{12}{100}×\frac{3}{10} = 90$.
答:全校获得二等奖的学生人数约为90.
22.(1)10 25 0.25
(2)解:补全频数分布直方图如答图所示.
(3)解:$2500×\frac{12}{100}×\frac{3}{10} = 90$.
答:全校获得二等奖的学生人数约为90.