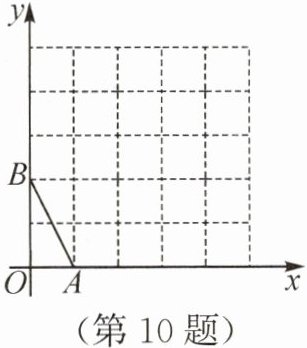
10. 在方格纸中,每个小方格的顶点称为格点,以格点的连线为边的三角形称为格点三角形.在如图所示的$5× 5$的方格纸中(每个小正方形的边长均为$1$),如果想作格点三角形$ABC$与三角形$OAB$相似(相似比不能为$1:1$),那么点$C$的坐标为
]
$(4,4)$或$(5,2)$
.
]
答案:10.$(4,4)$或$(5,2)$
解析:
解:由图可知,点$O(0,0)$,$A(1,0)$,$B(0,2)$,则$OA=1$,$OB=2$,$AB=\sqrt{(1-0)^2+(0-2)^2}=\sqrt{5}$。
因为$\triangle ABC$与$\triangle OAB$相似且相似比不为$1:1$,分两种情况:
情况一: 当$\triangle ABC ∼ \triangle OBA$时,$\frac{AB}{OB}=\frac{AC}{OA}=\frac{BC}{AB}$,即$\frac{\sqrt{5}}{2}=\frac{AC}{1}=\frac{BC}{\sqrt{5}}$,解得$AC=\frac{\sqrt{5}}{2}$(非格点,舍去)。
情况二: 当$\triangle ABC ∼ \triangle AOB$时,$\frac{AB}{AO}=\frac{AC}{BO}=\frac{BC}{AB}$,即$\frac{\sqrt{5}}{1}=\frac{AC}{2}=\frac{BC}{\sqrt{5}}$,解得$AC=2\sqrt{5}$,$BC=5$。
设$C(x,y)$,则$\sqrt{(x-1)^2+y^2}=2\sqrt{5}$,$\sqrt{x^2+(y-2)^2}=5$,解得$x=4$,$y=4$或$x=5$,$y=2$。
情况三: 当$\triangle ACB ∼ \triangle AOB$时,同理可得$C(4,4)$或$C(5,2)$。
综上,点$C$的坐标为$(4,4)$或$(5,2)$。
$(4,4)$或$(5,2)$
因为$\triangle ABC$与$\triangle OAB$相似且相似比不为$1:1$,分两种情况:
情况一: 当$\triangle ABC ∼ \triangle OBA$时,$\frac{AB}{OB}=\frac{AC}{OA}=\frac{BC}{AB}$,即$\frac{\sqrt{5}}{2}=\frac{AC}{1}=\frac{BC}{\sqrt{5}}$,解得$AC=\frac{\sqrt{5}}{2}$(非格点,舍去)。
情况二: 当$\triangle ABC ∼ \triangle AOB$时,$\frac{AB}{AO}=\frac{AC}{BO}=\frac{BC}{AB}$,即$\frac{\sqrt{5}}{1}=\frac{AC}{2}=\frac{BC}{\sqrt{5}}$,解得$AC=2\sqrt{5}$,$BC=5$。
设$C(x,y)$,则$\sqrt{(x-1)^2+y^2}=2\sqrt{5}$,$\sqrt{x^2+(y-2)^2}=5$,解得$x=4$,$y=4$或$x=5$,$y=2$。
情况三: 当$\triangle ACB ∼ \triangle AOB$时,同理可得$C(4,4)$或$C(5,2)$。
综上,点$C$的坐标为$(4,4)$或$(5,2)$。
$(4,4)$或$(5,2)$
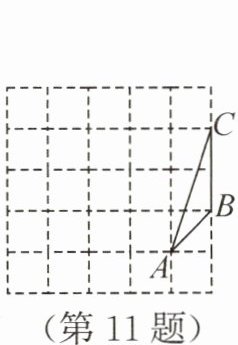
11. 如图,由$25$个边长为$1$的小正方形组成的正方形网格中有一个$\triangle ABC$,请在网格中画一个顶点在格点上,且与$\triangle ABC$相似的面积最大的$\triangle A'B'C'$,此时它的面积为
$5$
.
答案:
11.(画法不唯一)如图所示:

$5$解析:$S_{\triangle A'B'C'}=\frac{1}{2}×5×5 - \frac{1}{2}×1×3 - \frac{1}{2}×2×4 - 1×2 = 5$。故此时$\triangle A'B'C'$的面积为$5$。
11.(画法不唯一)如图所示:

$5$解析:$S_{\triangle A'B'C'}=\frac{1}{2}×5×5 - \frac{1}{2}×1×3 - \frac{1}{2}×2×4 - 1×2 = 5$。故此时$\triangle A'B'C'$的面积为$5$。
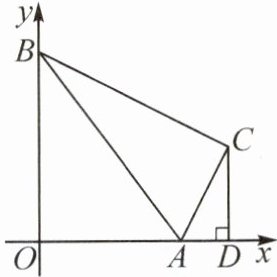
12. 如图,$\triangle ABC$各顶点的坐标分别为$A(3,0)$,$B(0,4)$,$C(4,2)$,过点$C$作$CD ⊥ x$轴,垂足为$D$.求证:$\angle ACD = \angle ABC$.
]

]
答案:12.过点$C$作$CH⊥ OB$于点$H$,则$\angle CHB=\angle CHO=90^{\circ}$。因为$CD⊥ x$轴,所以$\angle CDO=90^{\circ}$。又$\angle DOH=90^{\circ}$,所以四边形$CDOH$是矩形,所以$CD=OH$,$CH=OD$。因为$A(3,0)$,$B(0,4)$,$C(4,2)$,所以$OA=3$,$OB=4$,$CD=OH=2$,$CH=OD=4$,所以$AB=\sqrt{OA^{2}+OB^{2}}=5$,$AD=OD - OA = 1$,$BH=OB - OH = 2$,所以$AC=\sqrt{CD^{2}+AD^{2}}=\sqrt{5}$,$BC=\sqrt{CH^{2}+BH^{2}}=2\sqrt{5}$,所以$\frac{AD}{AC}=\frac{CD}{BC}=\frac{AC}{AB}=\frac{\sqrt{5}}{5}$,所以$\triangle ACD∼\triangle ABC$,所以$\angle ACD=\angle ABC$。
解析:
证明:过点$C$作$CH ⊥ OB$于点$H$,则$\angle CHB = \angle CHO = 90°$。
因为$CD ⊥ x$轴,所以$\angle CDO = 90°$。
又$\angle DOH = 90°$,所以四边形$CDOH$是矩形,因此$CD = OH$,$CH = OD$。
已知$A(3,0)$,$B(0,4)$,$C(4,2)$,
所以$OA = 3$,$OB = 4$,$CD = OH = 2$,$CH = OD = 4$。
计算得:
$AB = \sqrt{OA^2 + OB^2} = \sqrt{3^2 + 4^2} = 5$,
$AD = OD - OA = 4 - 3 = 1$,
$BH = OB - OH = 4 - 2 = 2$,
$AC = \sqrt{CD^2 + AD^2} = \sqrt{2^2 + 1^2} = \sqrt{5}$,
$BC = \sqrt{CH^2 + BH^2} = \sqrt{4^2 + 2^2} = 2\sqrt{5}$。
因为$\frac{AD}{AC} = \frac{1}{\sqrt{5}} = \frac{\sqrt{5}}{5}$,$\frac{CD}{BC} = \frac{2}{2\sqrt{5}} = \frac{\sqrt{5}}{5}$,$\frac{AC}{AB} = \frac{\sqrt{5}}{5}$,
所以$\frac{AD}{AC} = \frac{CD}{BC} = \frac{AC}{AB}$,
因此$\triangle ACD ∼ \triangle ABC$,
所以$\angle ACD = \angle ABC$。
因为$CD ⊥ x$轴,所以$\angle CDO = 90°$。
又$\angle DOH = 90°$,所以四边形$CDOH$是矩形,因此$CD = OH$,$CH = OD$。
已知$A(3,0)$,$B(0,4)$,$C(4,2)$,
所以$OA = 3$,$OB = 4$,$CD = OH = 2$,$CH = OD = 4$。
计算得:
$AB = \sqrt{OA^2 + OB^2} = \sqrt{3^2 + 4^2} = 5$,
$AD = OD - OA = 4 - 3 = 1$,
$BH = OB - OH = 4 - 2 = 2$,
$AC = \sqrt{CD^2 + AD^2} = \sqrt{2^2 + 1^2} = \sqrt{5}$,
$BC = \sqrt{CH^2 + BH^2} = \sqrt{4^2 + 2^2} = 2\sqrt{5}$。
因为$\frac{AD}{AC} = \frac{1}{\sqrt{5}} = \frac{\sqrt{5}}{5}$,$\frac{CD}{BC} = \frac{2}{2\sqrt{5}} = \frac{\sqrt{5}}{5}$,$\frac{AC}{AB} = \frac{\sqrt{5}}{5}$,
所以$\frac{AD}{AC} = \frac{CD}{BC} = \frac{AC}{AB}$,
因此$\triangle ACD ∼ \triangle ABC$,
所以$\angle ACD = \angle ABC$。
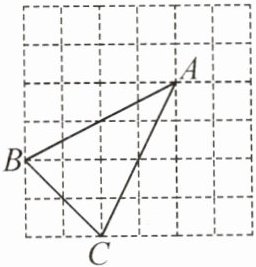
13. 在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,$\triangle ABC$是格点三角形,在如图所示的$6× 6$正方形网格中作出格点三角形$ADE$(不含$\triangle ABC$),使得$\triangle ADE \backsim \triangle ABC$(同一位置的格点三角形$ADE$只算一个),这样的格点三角形一共有(
A.$4$个
B.$5$个
C.$6$个
D.$7$个
C
)
A.$4$个
B.$5$个
C.$6$个
D.$7$个
答案:
13.C 解析:如图,使得$\triangle ADE∼\triangle ABC$的格点三角形一共有6个。
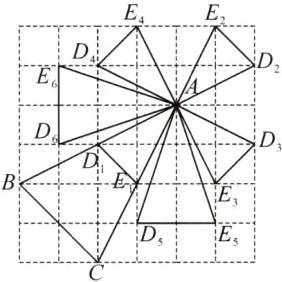
13.C 解析:如图,使得$\triangle ADE∼\triangle ABC$的格点三角形一共有6个。

14. 已知$\triangle ABC$的三边长分别为$6$,$7.5$,$9$,$\triangle DEF$的一边长为$4$,则当$\triangle DEF$的另两边长分别为
$5$,$6$或$3.2$,$4.8$或$\frac{8}{3}$,$\frac{10}{3}$
时,这两个三角形相似.答案:14.$5$,$6$或$3.2$,$4.8$或$\frac{8}{3}$,$\frac{10}{3}$ 解析:设$\triangle DEF$的另两边长分别为$x$和$y(x<y)$。由题意,得$\frac{4}{6}=\frac{x}{7.5}=\frac{y}{9}$或$\frac{4}{7.5}=\frac{x}{6}=\frac{y}{9}$或$\frac{4}{9}=\frac{x}{6}=\frac{y}{7.5}$,解得$x = 5$,$y = 6$或$x = 3.2$,$y = 4.8$或$x=\frac{8}{3}$,$y=\frac{10}{3}$。综上所述,当$\triangle DEF$的另两边长分别为$5$,$6$或$3.2$,$4.8$或$\frac{8}{3}$,$\frac{10}{3}$时,这两个三角形相似。
解析:
设$\triangle DEF$的另两边长分别为$x$和$y(x < y)$。
情况一:当$\triangle DEF$中长为$4$的边与$\triangle ABC$中长为$6$的边对应时,
$\frac{4}{6} = \frac{x}{7.5} = \frac{y}{9}$
解得$x = 5$,$y = 6$。
情况二:当$\triangle DEF$中长为$4$的边与$\triangle ABC$中长为$7.5$的边对应时,
$\frac{4}{7.5} = \frac{x}{6} = \frac{y}{9}$
解得$x = 3.2$,$y = 4.8$。
情况三:当$\triangle DEF$中长为$4$的边与$\triangle ABC$中长为$9$的边对应时,
$\frac{4}{9} = \frac{x}{6} = \frac{y}{7.5}$
解得$x = \frac{8}{3}$,$y = \frac{10}{3}$。
综上,$\triangle DEF$的另两边长分别为$5$,$6$或$3.2$,$4.8$或$\frac{8}{3}$,$\frac{10}{3}$。
情况一:当$\triangle DEF$中长为$4$的边与$\triangle ABC$中长为$6$的边对应时,
$\frac{4}{6} = \frac{x}{7.5} = \frac{y}{9}$
解得$x = 5$,$y = 6$。
情况二:当$\triangle DEF$中长为$4$的边与$\triangle ABC$中长为$7.5$的边对应时,
$\frac{4}{7.5} = \frac{x}{6} = \frac{y}{9}$
解得$x = 3.2$,$y = 4.8$。
情况三:当$\triangle DEF$中长为$4$的边与$\triangle ABC$中长为$9$的边对应时,
$\frac{4}{9} = \frac{x}{6} = \frac{y}{7.5}$
解得$x = \frac{8}{3}$,$y = \frac{10}{3}$。
综上,$\triangle DEF$的另两边长分别为$5$,$6$或$3.2$,$4.8$或$\frac{8}{3}$,$\frac{10}{3}$。
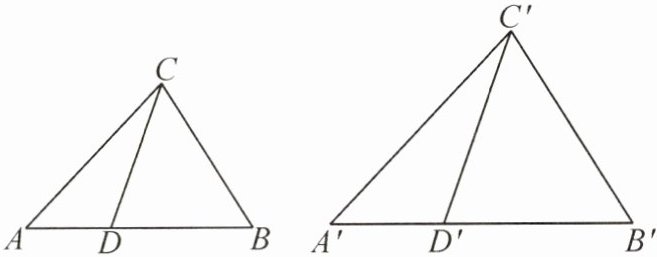
15. 新趋势 推导探究(2025·江苏苏州模拟)如图,在$\triangle ABC$和$\triangle A'B'C'$中,$D$,$D'$分别是$AB$,$A'B'$上一点,$\dfrac{AD}{AB} = \dfrac{A'D'}{A'B'}$.
(1)当$\dfrac{CD}{C'D'} = \dfrac{AC}{A'C'} = \dfrac{AB}{A'B'}$时,求证:$\triangle ABC \backsim \triangle A'B'C'$.证明的途径可以用下面的框图表示,请填写其中的空格:

(2)当$\dfrac{CD}{C'D'} = \dfrac{AC}{A'C'} = \dfrac{BC}{B'C'}$时,判断$\triangle ABC$与$\triangle A'B'C'$是否相似,并说明理由.
(1)当$\dfrac{CD}{C'D'} = \dfrac{AC}{A'C'} = \dfrac{AB}{A'B'}$时,求证:$\triangle ABC \backsim \triangle A'B'C'$.证明的途径可以用下面的框图表示,请填写其中的空格:

(2)当$\dfrac{CD}{C'D'} = \dfrac{AC}{A'C'} = \dfrac{BC}{B'C'}$时,判断$\triangle ABC$与$\triangle A'B'C'$是否相似,并说明理由.

答案:15.(1)$\frac{CD}{C'D'}=\frac{AC}{A'C'}=\frac{AD}{A'D'}$ $\angle A=\angle A'$
(2)$\triangle ABC∼\triangle A'B'C'$。理由如下:过点$D$,$D'$分别作$DE// BC$,$D'E'// B'C'$,$DE$交$AC$于点$E$,$D'E'$交$A'C'$于点$E'$。因为$DE// BC$,所以$\triangle ADE∼\triangle ABC$,所以$\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}$。同理可得$\frac{A'D'}{A'B'}=\frac{D'E'}{B'C'}$,所以$\frac{DE}{D'E'}=\frac{BC}{B'C'}$。同理可得$\frac{AE}{AC}=\frac{A'E'}{A'C'}$,所以$\frac{AC - AE}{AC}=\frac{A'C' - A'E'}{A'C'}$,即$\frac{EC}{AC}=\frac{E'C'}{A'C'}$,所以$\frac{EC}{E'C'}=\frac{AC}{A'C'}$。因为$\frac{CD}{C'D'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}$,所以$\frac{CD}{C'D'}=\frac{EC}{E'C'}=\frac{DE}{D'E'}$,所以$\triangle DCE∼\triangle D'C'E'$,所以$\angle CED=\angle C'E'D'$。因为$DE// BC$,所以$\angle CED+\angle ACB=180^{\circ}$。同理可得$\angle C'E'D'+\angle A'C'B'=180^{\circ}$,所以$\angle ACB=\angle A'C'B'$。又$\frac{AC}{A'C'}=\frac{BC}{B'C'}$,所以$\triangle ABC∼\triangle A'B'C'$。
(2)$\triangle ABC∼\triangle A'B'C'$。理由如下:过点$D$,$D'$分别作$DE// BC$,$D'E'// B'C'$,$DE$交$AC$于点$E$,$D'E'$交$A'C'$于点$E'$。因为$DE// BC$,所以$\triangle ADE∼\triangle ABC$,所以$\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}$。同理可得$\frac{A'D'}{A'B'}=\frac{D'E'}{B'C'}$,所以$\frac{DE}{D'E'}=\frac{BC}{B'C'}$。同理可得$\frac{AE}{AC}=\frac{A'E'}{A'C'}$,所以$\frac{AC - AE}{AC}=\frac{A'C' - A'E'}{A'C'}$,即$\frac{EC}{AC}=\frac{E'C'}{A'C'}$,所以$\frac{EC}{E'C'}=\frac{AC}{A'C'}$。因为$\frac{CD}{C'D'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}$,所以$\frac{CD}{C'D'}=\frac{EC}{E'C'}=\frac{DE}{D'E'}$,所以$\triangle DCE∼\triangle D'C'E'$,所以$\angle CED=\angle C'E'D'$。因为$DE// BC$,所以$\angle CED+\angle ACB=180^{\circ}$。同理可得$\angle C'E'D'+\angle A'C'B'=180^{\circ}$,所以$\angle ACB=\angle A'C'B'$。又$\frac{AC}{A'C'}=\frac{BC}{B'C'}$,所以$\triangle ABC∼\triangle A'B'C'$。