1. (2025·黑龙江绥化)若两个相似三角形的最长边分别为10 cm和6 cm,且它们的周长之和为48 cm,则较小三角形的周长为(
A.14 cm
B.18 cm
C.30 cm
D.34 cm
B
)A.14 cm
B.18 cm
C.30 cm
D.34 cm
答案:1. B
解析:
因为两个相似三角形的最长边分别为10 cm和6 cm,所以相似比为$10:6 = 5:3$。
设较小三角形的周长为$3x$ cm,较大三角形的周长为$5x$ cm。
已知它们的周长之和为48 cm,可得$3x + 5x = 48$,即$8x = 48$,解得$x = 6$。
所以较小三角形的周长为$3x = 3×6 = 18$ cm。
B
设较小三角形的周长为$3x$ cm,较大三角形的周长为$5x$ cm。
已知它们的周长之和为48 cm,可得$3x + 5x = 48$,即$8x = 48$,解得$x = 6$。
所以较小三角形的周长为$3x = 3×6 = 18$ cm。
B
2. (2025·江苏镇江模拟)如图,在边长为1的小正方形组成的网格中,A,B,C,D四个点均在格点上,AC与BD相交于点E,连接AB,CD,则△ABE与△CDE周长的比为(

A.1:4
B.4:1
C.1:2
D.2:1
D
)
A.1:4
B.4:1
C.1:2
D.2:1
答案:2. D
解析:
解:设每个小正方形边长为1,
由图可知,$A(0,3)$,$B(4,5)$,$C(3,2)$,$D(1,1)$,
$\overrightarrow{AB}=(4,2)$,$\overrightarrow{DC}=(2,1)$,
$\because \overrightarrow{AB}=2\overrightarrow{DC}$,$\therefore AB// DC$且$AB=2DC$,
$\therefore \triangle ABE\backsim \triangle CDE$,相似比为$2:1$,
$\therefore \triangle ABE$与$\triangle CDE$周长的比为$2:1$。
答案:D
由图可知,$A(0,3)$,$B(4,5)$,$C(3,2)$,$D(1,1)$,
$\overrightarrow{AB}=(4,2)$,$\overrightarrow{DC}=(2,1)$,
$\because \overrightarrow{AB}=2\overrightarrow{DC}$,$\therefore AB// DC$且$AB=2DC$,
$\therefore \triangle ABE\backsim \triangle CDE$,相似比为$2:1$,
$\therefore \triangle ABE$与$\triangle CDE$周长的比为$2:1$。
答案:D
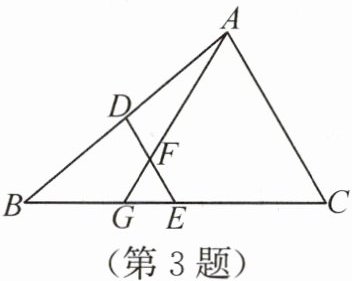
3. 如图,DE是△ABC的中位线,F是DE的中点,连接AF并延长交BC于点G.若$S_{△EFG}=1,$则△ABC的面积为(
A.16
B.18
C.24
D.32
C
)
A.16
B.18
C.24
D.32
答案:3. C 解析:过点D作DH//BC,交AG于点H,则∠FDH=∠FEG,∠FHD=∠FGE.因为F是DE的中点,所以DF=EF.在△DFH和△EFG中,$\begin{cases} ∠FHD=∠FGE,\\ ∠FDH=∠FEG,\\ DF=EF,\end{cases}$所以△DFH≌△EFG,所以FH=FG,S_△DFH=S_△EFG=1.因为DE是△ABC的中位线,所以D是AB的中点,所以AD=BD=$\frac{1}{2}$AB.因为DH//BC,所以△ADH∽△ABG,$\frac{AH}{HG}=\frac{AD}{BD}=1$,所以AH=HG=FH+FG=2FH,所以S_△ADH=2S_△DFH=2.因为$\frac{S_{△ADH}}{S_{△ABG}}=(\frac{AD}{AB})^2=\frac{1}{4}$,所以S_△ABG=8,所以S_四边形BDHG=S_△ABG - S_△ADH=6,所以S_△DBE=S_四边形BDFG+S_△EFG=S_四边形BDFG+S_△DFH=S_四边形BDHG=6.因为DE是△ABC的中位线,所以DE//AC,所以△DBE∽△ABC,所以$\frac{S_{△DBE}}{S_{△ABC}}=(\frac{DB}{AB})^2=\frac{1}{4}$,所以S_△ABC=24.故△ABC的面积为24.
4. (2024·重庆改编)若两个相似三角形的相似比为1:4,则这两个三角形面积的比为
1:16
.答案:4. 1:16
5. (教材P74习题2变式)如图,在△ABC中,D,E分别是边AB,AC上的点,且DE//BC.若△ADE与△ABC周长的比为2:3,AD=4,则DB=

]
2$\frac{1}{3}$
.
]
答案:5. 2$\frac{1}{3}$
解析:
证明:
∵DE//BC,
∴△ADE∽△ABC,
∵△ADE与△ABC周长的比为2:3,
∴相似比为$\frac{AD}{AB}=\frac{2}{3}$,
∵AD=4,
∴$\frac{4}{AB}=\frac{2}{3}$,
解得AB=6,
∴DB=AB-AD=6-4=2。
∵DE//BC,
∴△ADE∽△ABC,
∵△ADE与△ABC周长的比为2:3,
∴相似比为$\frac{AD}{AB}=\frac{2}{3}$,
∵AD=4,
∴$\frac{4}{AB}=\frac{2}{3}$,
解得AB=6,
∴DB=AB-AD=6-4=2。
6. 如图,已知等边三角形ABC被有一条边平行于BC的矩形所截,AB被截成三等份,则阴影部分的面积是△ABC面积的

$\frac{1}{3}$
.
答案:6. $\frac{1}{3}$ 解析:由题意,得EH//FG//BC,所以△AEH∽△AFG∽△ABC.因为AE=EF=BF,所以$\frac{AF}{AB}=\frac{2}{3}$,$\frac{AE}{AB}=\frac{1}{3}$,所以$\frac{S_{△AFG}}{S_{△ABC}}=(\frac{AF}{AB})^2=\frac{4}{9}$,$S_{△AEH}=(\frac{AE}{AB})^2=\frac{1}{9}$,所以S_△AFG=$\frac{4}{9}$S_△ABC,S_△AEH=$\frac{1}{9}$S_△ABC,所以S_阴影=S_△AFG - S_△AEH=$\frac{1}{3}$S_△ABC.故阴影部分的面积是△ABC面积的$\frac{1}{3}$.
解析:
解:由题意得$EH // FG // BC$,故$\triangle AEH ∼ \triangle AFG ∼ \triangle ABC$。
因为$AE=EF=BF$,所以$\frac{AE}{AB}=\frac{1}{3}$,$\frac{AF}{AB}=\frac{2}{3}$。
根据相似三角形面积比等于相似比的平方,可得:
$\frac{S_{\triangle AEH}}{S_{\triangle ABC}}=(\frac{AE}{AB})^2=(\frac{1}{3})^2=\frac{1}{9}$,则$S_{\triangle AEH}=\frac{1}{9}S_{\triangle ABC}$;
$\frac{S_{\triangle AFG}}{S_{\triangle ABC}}=(\frac{AF}{AB})^2=(\frac{2}{3})^2=\frac{4}{9}$,则$S_{\triangle AFG}=\frac{4}{9}S_{\triangle ABC}$。
所以阴影部分面积$S_{\mathrm{阴影}}=S_{\triangle AFG}-S_{\triangle AEH}=\frac{4}{9}S_{\triangle ABC}-\frac{1}{9}S_{\triangle ABC}=\frac{3}{9}S_{\triangle ABC}=\frac{1}{3}S_{\triangle ABC}$。
故阴影部分的面积是$\triangle ABC$面积的$\frac{1}{3}$。
因为$AE=EF=BF$,所以$\frac{AE}{AB}=\frac{1}{3}$,$\frac{AF}{AB}=\frac{2}{3}$。
根据相似三角形面积比等于相似比的平方,可得:
$\frac{S_{\triangle AEH}}{S_{\triangle ABC}}=(\frac{AE}{AB})^2=(\frac{1}{3})^2=\frac{1}{9}$,则$S_{\triangle AEH}=\frac{1}{9}S_{\triangle ABC}$;
$\frac{S_{\triangle AFG}}{S_{\triangle ABC}}=(\frac{AF}{AB})^2=(\frac{2}{3})^2=\frac{4}{9}$,则$S_{\triangle AFG}=\frac{4}{9}S_{\triangle ABC}$。
所以阴影部分面积$S_{\mathrm{阴影}}=S_{\triangle AFG}-S_{\triangle AEH}=\frac{4}{9}S_{\triangle ABC}-\frac{1}{9}S_{\triangle ABC}=\frac{3}{9}S_{\triangle ABC}=\frac{1}{3}S_{\triangle ABC}$。
故阴影部分的面积是$\triangle ABC$面积的$\frac{1}{3}$。
7. 如图,在△ABC中,DE//BC,EF//AB.若$S_{△ADE}=4,S_{△EFC}=9,$求△ABC的面积.


答案:7. 因为DE//BC,所以△ADE∽△ABC.因为EF//AB,所以△EFC∽△ABC,所以△ADE∽△EFC.因为S_△ADE=4,S_△EFC=9,所以$\frac{S_{△ADE}}{S_{△EFC}}=(\frac{AE}{EC})^2=\frac{4}{9}$,所以$\frac{AE}{EC}=\frac{2}{3}$,所以$\frac{AE}{AC}=\frac{2}{5}$,所以$\frac{S_{△ADE}}{S_{△ABC}}=(\frac{AE}{AC})^2=\frac{4}{25}$,所以S_△ABC=25.故△ABC的面积是25.
解析:
证明:因为 $DE // BC$,所以 $\triangle ADE ∼ \triangle ABC$。
因为 $EF // AB$,所以 $\triangle EFC ∼ \triangle ABC$,故 $\triangle ADE ∼ \triangle EFC$。
已知 $S_{\triangle ADE}=4$,$S_{\triangle EFC}=9$,则 $\frac{S_{\triangle ADE}}{S_{\triangle EFC}} = (\frac{AE}{EC})^2 = \frac{4}{9}$,
所以 $\frac{AE}{EC} = \frac{2}{3}$,从而 $\frac{AE}{AC} = \frac{AE}{AE+EC} = \frac{2}{2+3} = \frac{2}{5}$。
因为 $\triangle ADE ∼ \triangle ABC$,所以 $\frac{S_{\triangle ADE}}{S_{\triangle ABC}} = (\frac{AE}{AC})^2 = (\frac{2}{5})^2 = \frac{4}{25}$,
因此 $S_{\triangle ABC} = 25$。
故 $\triangle ABC$ 的面积是 $25$。
因为 $EF // AB$,所以 $\triangle EFC ∼ \triangle ABC$,故 $\triangle ADE ∼ \triangle EFC$。
已知 $S_{\triangle ADE}=4$,$S_{\triangle EFC}=9$,则 $\frac{S_{\triangle ADE}}{S_{\triangle EFC}} = (\frac{AE}{EC})^2 = \frac{4}{9}$,
所以 $\frac{AE}{EC} = \frac{2}{3}$,从而 $\frac{AE}{AC} = \frac{AE}{AE+EC} = \frac{2}{2+3} = \frac{2}{5}$。
因为 $\triangle ADE ∼ \triangle ABC$,所以 $\frac{S_{\triangle ADE}}{S_{\triangle ABC}} = (\frac{AE}{AC})^2 = (\frac{2}{5})^2 = \frac{4}{25}$,
因此 $S_{\triangle ABC} = 25$。
故 $\triangle ABC$ 的面积是 $25$。
8. 新素养 几何直观 如图,在□ABCD中,点E在边DC上,DE:CE=3:1,连接AE,BD交于点F,则△DEF与△BAF面积的比为(

A.3:4
B.9:16
C.9:1
D.3:1
B
)
A.3:4
B.9:16
C.9:1
D.3:1
答案:8. B
解析:
证明:
∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,
∴∠EDF=∠ABF,∠DEF=∠BAF,
∴△DEF∽△BAF,
∵DE:CE=3:1,
∴DE:DC=3:4,
∵AB=CD,
∴DE:AB=3:4,
∴$\frac{S_{\triangle DEF}}{S_{\triangle BAF}}=(\frac{DE}{AB})^2=(\frac{3}{4})^2=\frac{9}{16}$,
即△DEF与△BAF面积的比为9:16。
答案:B
∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,
∴∠EDF=∠ABF,∠DEF=∠BAF,
∴△DEF∽△BAF,
∵DE:CE=3:1,
∴DE:DC=3:4,
∵AB=CD,
∴DE:AB=3:4,
∴$\frac{S_{\triangle DEF}}{S_{\triangle BAF}}=(\frac{DE}{AB})^2=(\frac{3}{4})^2=\frac{9}{16}$,
即△DEF与△BAF面积的比为9:16。
答案:B
9. 如图,在△ABC中,D是边AB上的点,∠B=∠ACD,AC:AB=1:2,则△ADC与△ACB周长的比是(

A.1:√{2}
B.1:2
C.1:3
D.1:4
B
)
A.1:√{2}
B.1:2
C.1:3
D.1:4
答案:9. B
解析:
证明:在△ABC和△ACD中,
∵∠B=∠ACD,∠A=∠A,
∴△ABC∽△ACD,
∵AC:AB=1:2,
∴△ADC与△ACB的相似比为1:2,
∴△ADC与△ACB周长的比是1:2。
答案:B
∵∠B=∠ACD,∠A=∠A,
∴△ABC∽△ACD,
∵AC:AB=1:2,
∴△ADC与△ACB的相似比为1:2,
∴△ADC与△ACB周长的比是1:2。
答案:B
10. 如图,△ABO的顶点A在函数y=k/x(x>0)的图像上,顶点B在x轴上,∠ABO=90°,过边AO的三等分点M,N分别作x轴的平行线交AB于点P,Q.若四边形MNQP的面积为3,则k的值为(

A.9
B.12
C.15
D.18
D
)
A.9
B.12
C.15
D.18
答案:10. D 解析:因为NQ//MP//OB,所以△ANQ∽△AMP∽△AOB.因为M,N是AO的三等分点,所以$\frac{AN}{AM}=\frac{1}{2}$,$\frac{AN}{AO}=\frac{1}{3}$,所以$\frac{S_{△ANQ}}{S_{△AMP}}=(\frac{AN}{AM})^2=\frac{1}{4}$,所以$\frac{S_{△ANQ}}{S_{四边形MNQP}}=\frac{1}{3}$.因为S_四边形MNQP=3,所以S_△ANQ=1.因为$\frac{S_{△ANQ}}{S_{△AOB}}=(\frac{AN}{AO})^2=\frac{1}{9}$,所以S_△AOB=9.设A(m,n),则OB=m,AB=n,所以S_△AOB=$\frac{1}{2}$OB·AB=$\frac{1}{2}mn=9$,所以mn=18.因为点A在函数y=$\frac{k}{x}$的图像上,所以k=mn=18.