1. 已知$\triangle ABC \backsim \triangle A'B'C'$,$AD$和$A'D'$是它们的对应中线。若$AD = 10$,$A'D' = 6$,则$\triangle ABC$与$\triangle A'B'C'$周长的比是(
A.$3:5$
B.$9:25$
C.$5:3$
D.$25:9$
C
)A.$3:5$
B.$9:25$
C.$5:3$
D.$25:9$
答案:1. C
解析:
∵$\triangle ABC \backsim \triangle A'B'C'$,AD和$A'D'$是对应中线,
∴$\triangle ABC$与$\triangle A'B'C'$的相似比等于对应中线的比,即$\frac{AD}{A'D'}=\frac{10}{6}=\frac{5}{3}$。
又
∵相似三角形的周长比等于相似比,
∴$\triangle ABC$与$\triangle A'B'C'$周长的比是$5:3$。
C
2. 若两个相似三角形的一组对应高分别为$15$和$5$,面积之差为$80$,则较大三角形的面积为(
A.$90$
B.$180$
C.$270$
D.$360$
A
)A.$90$
B.$180$
C.$270$
D.$360$
答案:2. A
解析:
∵两个相似三角形的一组对应高分别为15和5,
∴相似比为$15:5 = 3:1$。
∵相似三角形面积比等于相似比的平方,
∴面积比为$3^2:1^2 = 9:1$。
设较大三角形面积为$9x$,较小三角形面积为$x$,
由面积之差为80,得$9x - x = 80$,
解得$x = 10$,
则较大三角形面积为$9x = 9×10 = 90$。
A
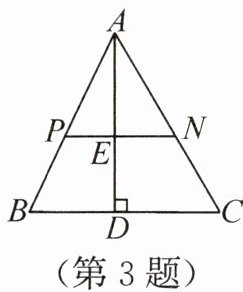
3. (2025·江苏扬州模拟)如图,$P$,$N$分别是$\triangle ABC$的边$AB$,$AC$上的点,且$PN // BC$,$AD ⊥ BC$交$PN$于点$E$,交$BC$于点$D$。若$\frac{S_{\triangle APN}}{S_{四边形BCNP}} = \frac{1}{2}$,则$\frac{AE}{AD}$的值为(
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{\sqrt{2}}{2}$
D.$\frac{\sqrt{3}}{3}$
D
)
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{\sqrt{2}}{2}$
D.$\frac{\sqrt{3}}{3}$
答案:3. D 解析:因为 $PN // BC$,所以$\triangle APN ∼ \triangle ABC$. 因为$\frac{S_{\triangle APN}}{S_{\mathrm{四边形}BCNP}} = \frac{1}{2}$,所以$\frac{S_{\triangle APN}}{S_{\triangle ABC}} = \frac{1}{3}$. 因为$\frac{S_{\triangle APN}}{S_{\triangle ABC}} = (\frac{AP}{AB})^2$,所以$(\frac{AP}{AB})^2 = \frac{1}{3}$,所以$\frac{AP}{AB} = \frac{\sqrt{3}}{3}$. 因为$AD ⊥ BC$,所以$AE ⊥ PN$,所以$AE, AD$ 分别是$\triangle APN$ 和$\triangle ABC$ 的对应高,所以$\frac{AE}{AD} = \frac{AP}{AB} = \frac{\sqrt{3}}{3}$.
4. 若$\triangle ABC \backsim \triangle DEF$,且对应高的比为$2:3$,则$\triangle ABC$和$\triangle DEF$面积的比为
$4:9$
。答案:4. $4:9$
5. (2025·甘肃)“儿童散学归来早,忙趁东风放纸鸢。”风筝古称纸鸢,起源于春秋战国时期,风筝制作技艺已被列入国家非物质文化遗产名录。为丰富校园生活,某校开展风筝制作活动,小言和哥哥制作了一大一小两个形状相同的风筝。风筝的形状如图所示,其中对角线$AC ⊥ BD$。已知大、小风筝对应边的比为$3:1$,且小风筝两条对角线的长分别为$30\mathrm{cm}$和$35\mathrm{cm}$,则大风筝两条对角线长的和为

$195$
$\mathrm{cm}$。
答案:5. $195$
解析:
解:因为大、小风筝形状相同,对应边的比为$3:1$,所以大、小风筝的相似比为$3:1$。
由于相似图形对应对角线的比等于相似比,小风筝两条对角线的长分别为$30\mathrm{cm}$和$35\mathrm{cm}$,则大风筝两条对角线的长分别为$30×3 = 90\mathrm{cm}$和$35×3 = 105\mathrm{cm}$。
所以大风筝两条对角线长的和为$90 + 105 = 195\mathrm{cm}$。
答案:$195$
由于相似图形对应对角线的比等于相似比,小风筝两条对角线的长分别为$30\mathrm{cm}$和$35\mathrm{cm}$,则大风筝两条对角线的长分别为$30×3 = 90\mathrm{cm}$和$35×3 = 105\mathrm{cm}$。
所以大风筝两条对角线长的和为$90 + 105 = 195\mathrm{cm}$。
答案:$195$
6. 已知两个相似三角形面积的比为$4:1$。如果这两个三角形最短边上的中线长之差为$9$,那么这两条中线长之和为
$27$
。答案:6. $27$ 解析:因为这两个相似三角形面积的比为 $4:1$,所以这两个相似三角形的相似比为 $2:1$. 因为这两个三角形最短边上的中线长之差为 $9$,所以这两条中线长分别为 $9 × \frac{1}{2 - 1} = 9$ 和 $9 × \frac{2}{2 - 1} = 18$,所以这两条中线长之和为 $9 + 18 = 27$.
解析:
因为两个相似三角形面积的比为$4:1$,所以相似比为$\sqrt{4}:\sqrt{1}=2:1$。
设较短中线长为$x$,则较长中线长为$2x$。
由中线长之差为$9$,得$2x - x = 9$,解得$x = 9$。
较长中线长为$2x = 18$,两条中线长之和为$9 + 18 = 27$。
$27$
设较短中线长为$x$,则较长中线长为$2x$。
由中线长之差为$9$,得$2x - x = 9$,解得$x = 9$。
较长中线长为$2x = 18$,两条中线长之和为$9 + 18 = 27$。
$27$
7. (教材P73练习3变式)如图,一块材料的形状是锐角三角形$ABC$,边$BC = 120\mathrm{mm}$,高$AD = 80\mathrm{mm}$,把它加工成正方形零件,使正方形的一边在$BC$上,其余两个顶点分别在$AB$,$AC$上,求这个正方形零件的边长。


答案:7. 因为四边形 $EFHG$ 是正方形,所以 $EF // BC$,所以$\triangle AEF ∼ \triangle ABC$. 因为 $AD$ 是$\triangle ABC$ 的高,所以$AD ⊥ BC$,所以$AK ⊥ EF$,所以$AK, AD$ 分别是$\triangle AEF$ 和$\triangle ABC$ 的对应高,所以$\frac{AK}{AD} = \frac{EF}{BC}$. 设这个正方形零件的边长是 $x \mathrm{ mm}$,则 $EF = DK = x \mathrm{ mm}$. 因为$AD = 80 \mathrm{ mm}$,所以$AK = AD - DK = (80 - x) \mathrm{ mm}$. 因为$BC = 120 \mathrm{ mm}$,所以$\frac{80 - x}{80} = \frac{x}{120}$,解得 $x = 48$. 故这个正方形零件的边长是 $48 \mathrm{ mm}$.
解析:
解:设正方形零件的边长为 $ x \, \mathrm{mm} $。
因为四边形 $ EFHG $ 是正方形,所以 $ EF // BC $,$ EF = x \, \mathrm{mm} $,$ KD = x \, \mathrm{mm} $。
由于 $ EF // BC $,可得 $ \triangle AEF ∼ \triangle ABC $。
因为 $ AD $ 是 $ \triangle ABC $ 的高,所以 $ AK $ 是 $ \triangle AEF $ 的高,且 $ AK = AD - KD = (80 - x) \, \mathrm{mm} $。
根据相似三角形对应高的比等于相似比,有:
$\frac{AK}{AD} = \frac{EF}{BC}$
代入数据:
$\frac{80 - x}{80} = \frac{x}{120}$
解得:
$x = 48$
故这个正方形零件的边长是 $ 48 \, \mathrm{mm} $。
因为四边形 $ EFHG $ 是正方形,所以 $ EF // BC $,$ EF = x \, \mathrm{mm} $,$ KD = x \, \mathrm{mm} $。
由于 $ EF // BC $,可得 $ \triangle AEF ∼ \triangle ABC $。
因为 $ AD $ 是 $ \triangle ABC $ 的高,所以 $ AK $ 是 $ \triangle AEF $ 的高,且 $ AK = AD - KD = (80 - x) \, \mathrm{mm} $。
根据相似三角形对应高的比等于相似比,有:
$\frac{AK}{AD} = \frac{EF}{BC}$
代入数据:
$\frac{80 - x}{80} = \frac{x}{120}$
解得:
$x = 48$
故这个正方形零件的边长是 $ 48 \, \mathrm{mm} $。
8. 如图,将矩形纸片$ABCD$沿$GH$对折,点$C$落在点$Q$处,点$D$落在边$AB$上的点$E$处,$EQ$与$BC$相交于点$F$。若$AD = 8$,$AB = 6$,$AE = 4$,则$\triangle EBF$的周长为(

A.$7$
B.$8$
C.$9$
D.$10$
B
)
A.$7$
B.$8$
C.$9$
D.$10$
答案:8. B
解析:
解:设 $DG = EG = x$,则 $AG = AD - DG = 8 - x$。
在 $Rt\triangle AEG$ 中,$AE = 4$,由勾股定理得:$AE^2 + AG^2 = EG^2$,即 $4^2 + (8 - x)^2 = x^2$,解得 $x = 5$,故 $AG = 3$。
设 $AH = y$,则 $DH = EH = 8 - y$。在 $Rt\triangle AEH$ 中,$AE = 4$,由勾股定理得:$AE^2 + AH^2 = EH^2$,即 $4^2 + y^2 = (8 - y)^2$,解得 $y = 3$,故 $AH = 3$,$EH = 5$。
$\tan\angle AEH = \frac{AH}{AE} = \frac{3}{4}$,则 $\angle BEF = 90° - \angle AEH$,$\tan\angle BEF = \frac{4}{3}$。
设 $BF = 3k$,$BE = AB - AE = 2$,在 $Rt\triangle BEF$ 中,$\tan\angle BEF = \frac{BF}{BE} = \frac{3k}{2} = \frac{4}{3}$,解得 $k = \frac{8}{9}$,则 $BF = \frac{8}{3}$,$EF = \frac{10}{3}$。
$\triangle EBF$ 的周长为 $BE + BF + EF = 2 + \frac{8}{3} + \frac{10}{3} = 8$。
答案:B
在 $Rt\triangle AEG$ 中,$AE = 4$,由勾股定理得:$AE^2 + AG^2 = EG^2$,即 $4^2 + (8 - x)^2 = x^2$,解得 $x = 5$,故 $AG = 3$。
设 $AH = y$,则 $DH = EH = 8 - y$。在 $Rt\triangle AEH$ 中,$AE = 4$,由勾股定理得:$AE^2 + AH^2 = EH^2$,即 $4^2 + y^2 = (8 - y)^2$,解得 $y = 3$,故 $AH = 3$,$EH = 5$。
$\tan\angle AEH = \frac{AH}{AE} = \frac{3}{4}$,则 $\angle BEF = 90° - \angle AEH$,$\tan\angle BEF = \frac{4}{3}$。
设 $BF = 3k$,$BE = AB - AE = 2$,在 $Rt\triangle BEF$ 中,$\tan\angle BEF = \frac{BF}{BE} = \frac{3k}{2} = \frac{4}{3}$,解得 $k = \frac{8}{9}$,则 $BF = \frac{8}{3}$,$EF = \frac{10}{3}$。
$\triangle EBF$ 的周长为 $BE + BF + EF = 2 + \frac{8}{3} + \frac{10}{3} = 8$。
答案:B
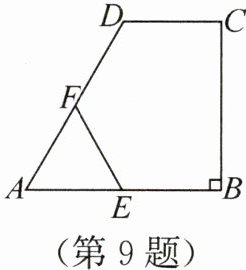
9. 如图,在四边形$ABCD$中,$DC // AB$,$CB ⊥ AB$,$AB = AD$,$CD = \frac{1}{2}AB$,$E$,$F$分别为$AB$,$AD$的中点,则$\triangle AEF$与五边形$BCDFE$面积的比为(
A.$1:7$
B.$1:6$
C.$1:5$
D.$1:4$
C
)
A.$1:7$
B.$1:6$
C.$1:5$
D.$1:4$
答案:9. C 解析:连接 $BD$. 因为 $E, F$ 分别为 $AB, AD$ 的中点,所以 $EF$ 是$\triangle ABD$ 的中位线,所以$EF = \frac{1}{2}BD, EF // BD$,所以$\triangle AEF ∼ \triangle ABD$,所以$\frac{S_{\triangle AEF}}{S_{\triangle ABD}} = (\frac{EF}{BD})^2 = \frac{1}{4}$,所以$S_{\triangle ABD} = 4S_{\triangle AEF}$,所以$S_{\mathrm{四边形}EFDB} = 3S_{\triangle AEF}$. 因为$CD = \frac{1}{2}AB, AB // CD$,所以$\frac{S_{\triangle CDB}}{S_{\triangle ABD}} = \frac{CD}{AB} = \frac{1}{2}$,所以$S_{\triangle CDB} = \frac{1}{2}S_{\triangle ABD} = 2S_{\triangle AEF}$,所以$S_{\mathrm{五边形}BCDEF} = S_{\mathrm{四边形}EFDB} + S_{\triangle CDB} = 5S_{\triangle AEF}$,所以$S_{\triangle AEF}:S_{\mathrm{五边形}BCDEF} = 1:5$. 故$\triangle AEF$ 与五边形 $BCDEF$ 面积的比为 $1:5$.