9. (2024·内蒙古包头)如图,在矩形ABCD中,E,F是边BC上两点,且BE=EF=FC,连接DE,AF,DE与AF相交于点G,连接BG.若AB=4,BC=6,则sin∠GBF的值为(

A.$\frac{\sqrt{10}}{10}$
B.$\frac{3\sqrt{10}}{10}$
C.$\frac{1}{3}$
D.$\frac{2}{3}$
A
)
A.$\frac{\sqrt{10}}{10}$
B.$\frac{3\sqrt{10}}{10}$
C.$\frac{1}{3}$
D.$\frac{2}{3}$
答案:9.A
解析:
解:以B为原点,BC为x轴,BA为y轴建立坐标系。
∵AB=4,BC=6,BE=EF=FC,
∴B(0,0),E(2,0),F(4,0),C(6,0),A(0,4),D(6,4)。
直线AF:过A(0,4),F(4,0),斜率$k_{AF}=\frac{0-4}{4-0}=-1$,方程为$y=-x+4$。
直线DE:过D(6,4),E(2,0),斜率$k_{DE}=\frac{0-4}{2-6}=1$,方程为$y-0=1×(x-2)$,即$y=x-2$。
联立$\begin{cases}y=-x+4\\y=x-2\end{cases}$,解得$x=3$,$y=1$,
∴G(3,1)。
过G作GH⊥BC于H,H(3,0),则GH=1,BH=3,FH=4-3=1。
在Rt△GHF中,$GF=\sqrt{GH^2+FH^2}=\sqrt{1^2+1^2}=\sqrt{2}$。
在△GBF中,由正弦定理:$\frac{GF}{\sin\angle GBF}=\frac{BG}{\sin\angle GFB}$。
$BG=\sqrt{BH^2+GH^2}=\sqrt{3^2+1^2}=\sqrt{10}$,$\sin\angle GFB=\frac{GH}{GF}=\frac{1}{\sqrt{2}}$。
∴$\sin\angle GBF=\frac{GF·\sin\angle GFB}{BG}=\frac{\sqrt{2}·\frac{1}{\sqrt{2}}}{\sqrt{10}}=\frac{1}{\sqrt{10}}=\frac{\sqrt{10}}{10}$。
答案:A
∵AB=4,BC=6,BE=EF=FC,
∴B(0,0),E(2,0),F(4,0),C(6,0),A(0,4),D(6,4)。
直线AF:过A(0,4),F(4,0),斜率$k_{AF}=\frac{0-4}{4-0}=-1$,方程为$y=-x+4$。
直线DE:过D(6,4),E(2,0),斜率$k_{DE}=\frac{0-4}{2-6}=1$,方程为$y-0=1×(x-2)$,即$y=x-2$。
联立$\begin{cases}y=-x+4\\y=x-2\end{cases}$,解得$x=3$,$y=1$,
∴G(3,1)。
过G作GH⊥BC于H,H(3,0),则GH=1,BH=3,FH=4-3=1。
在Rt△GHF中,$GF=\sqrt{GH^2+FH^2}=\sqrt{1^2+1^2}=\sqrt{2}$。
在△GBF中,由正弦定理:$\frac{GF}{\sin\angle GBF}=\frac{BG}{\sin\angle GFB}$。
$BG=\sqrt{BH^2+GH^2}=\sqrt{3^2+1^2}=\sqrt{10}$,$\sin\angle GFB=\frac{GH}{GF}=\frac{1}{\sqrt{2}}$。
∴$\sin\angle GBF=\frac{GF·\sin\angle GFB}{BG}=\frac{\sqrt{2}·\frac{1}{\sqrt{2}}}{\sqrt{10}}=\frac{1}{\sqrt{10}}=\frac{\sqrt{10}}{10}$。
答案:A
10. 新趋势传统文化(2023·内蒙古包头)如图是源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为α,则cosα的值为(

A.$\frac{3}{4}$
B.$\frac{4}{3}$
C.$\frac{3}{5}$
D.$\frac{4}{5}$
D
)
A.$\frac{3}{4}$
B.$\frac{4}{3}$
C.$\frac{3}{5}$
D.$\frac{4}{5}$
答案:10.D 解析:设直角三角形两条直角边的长分别为$a$,$b$,其中$a>b$.因为小正方形的面积为1,所以小正方形的边长为1,所以$a - b = 1$,所以$a = b + 1$.因为大正方形的面积为25,所以大正方形的边长为5,且$a^{2}+b^{2}=25$,所以$(b + 1)^{2}+b^{2}=25$,解得$b_{1}=3$,$b_{2}=-4$(不合题意,舍去),所以$a = 4$,所以$\cos\alpha=\frac{4}{5}$.
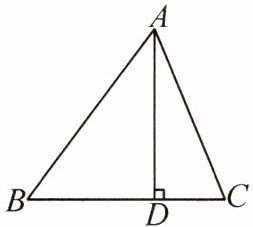
11. (2025·江苏盐城模拟)如图,在△ABC中,AD⊥BC于点D.若BC=14,AD=12,tan∠BAD=$\frac{3}{4}$,则sinC的值为
$\frac{12}{13}$
.
答案:11.$\frac{12}{13}$
解析:
解:在Rt△ABD中,AD⊥BC,AD=12,tan∠BAD=$\frac{BD}{AD}=\frac{3}{4}$,
则$\frac{BD}{12}=\frac{3}{4}$,解得BD=9.
∵BC=14,
∴DC=BC-BD=14-9=5.
在Rt△ADC中,AC=$\sqrt{AD^2+DC^2}=\sqrt{12^2+5^2}=13$,
∴sinC=$\frac{AD}{AC}=\frac{12}{13}$.
则$\frac{BD}{12}=\frac{3}{4}$,解得BD=9.
∵BC=14,
∴DC=BC-BD=14-9=5.
在Rt△ADC中,AC=$\sqrt{AD^2+DC^2}=\sqrt{12^2+5^2}=13$,
∴sinC=$\frac{AD}{AC}=\frac{12}{13}$.
12. 在直角三角形ABC中,若AC=2AB,则cosC=
$\frac{\sqrt{3}}{2}$或$\frac{2\sqrt{5}}{5}$
.答案:12.$\frac{\sqrt{3}}{2}$或$\frac{2\sqrt{5}}{5}$ 解析:设$AB = x$.因为$AC = 2AB$,所以$AC = 2x$.分类讨论如下:①若$\angle B = 90^{\circ}$,则$BC=\sqrt{AC^{2}-AB^{2}}=\sqrt{3}x$,所以$\cos C=\frac{BC}{AC}=\frac{\sqrt{3}}{2}$;②若$\angle A = 90^{\circ}$,则$BC=\sqrt{AB^{2}+AC^{2}}=\sqrt{5}x$,所以$\cos C=\frac{AC}{BC}=\frac{2\sqrt{5}}{5}$.综上所述,$\cos C=\frac{\sqrt{3}}{2}$或$\frac{2\sqrt{5}}{5}$.
易错警示:注意分类讨论,避免漏解.
易错警示:注意分类讨论,避免漏解.
13. 新趋势推导探究如图①,在Rt△ABC中,以下是小亮探索$\frac{a}{\sin A}$与$\frac{b}{\sin B}$之间关系的方法:因为sinA=$\frac{a}{c}$,sinB=$\frac{b}{c}$,所以c=$\frac{a}{\sin A}$,c=$\frac{b}{\sin B}$,所以$\frac{a}{\sin A}=\frac{b}{\sin B}$.根据你掌握的三角函数知识,在图②所示的锐角三角形ABC中,探索$\frac{a}{\sin A}$,$\frac{b}{\sin B}$,$\frac{c}{\sin C}$之间的关系,并写出探索过程.


答案:
13.如图①,过点A作边BC上的高AD.因为在$\mathrm{Rt}\triangle ABD$中,$\sin B=\frac{AD}{c}$,在$\mathrm{Rt}\triangle ACD$中,$\sin C=\frac{AD}{b}$,所以$AD = c\sin B$,$AD = b\sin C$,所以$c\sin B = b\sin C$,所以$\frac{b}{\sin B}=\frac{c}{\sin C}$.如图②,过点B作边AC上的高BE.因为在$\mathrm{Rt}\triangle ABE$中,$\sin A=\frac{BE}{c}$,在$\mathrm{Rt}\triangle BCE$中,$\sin C=\frac{BE}{a}$,所以$BE = c\sin A$,$BE = a\sin C$,所以$c\sin A = a\sin C$,所以$\frac{a}{\sin A}=\frac{c}{\sin C}$,所以$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$.

13.如图①,过点A作边BC上的高AD.因为在$\mathrm{Rt}\triangle ABD$中,$\sin B=\frac{AD}{c}$,在$\mathrm{Rt}\triangle ACD$中,$\sin C=\frac{AD}{b}$,所以$AD = c\sin B$,$AD = b\sin C$,所以$c\sin B = b\sin C$,所以$\frac{b}{\sin B}=\frac{c}{\sin C}$.如图②,过点B作边AC上的高BE.因为在$\mathrm{Rt}\triangle ABE$中,$\sin A=\frac{BE}{c}$,在$\mathrm{Rt}\triangle BCE$中,$\sin C=\frac{BE}{a}$,所以$BE = c\sin A$,$BE = a\sin C$,所以$c\sin A = a\sin C$,所以$\frac{a}{\sin A}=\frac{c}{\sin C}$,所以$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$.

14. 如图,在矩形纸片ABCD中,AB=4,BC=3,点P在边BC上,将△CDP沿DP折叠,点C落在点E处,PE,DE分别交AB于点O,F,且OP=OF,则cos∠ADF的值为(

A.$\frac{11}{13}$
B.$\frac{13}{15}$
C.$\frac{15}{17}$
D.$\frac{17}{19}$
C
)
A.$\frac{11}{13}$
B.$\frac{13}{15}$
C.$\frac{15}{17}$
D.$\frac{17}{19}$
答案:14.C 解析:因为四边形ABCD是矩形,所以$DC = AB = 4$,$AD = BC = 3$,$\angle A=\angle B=\angle C = 90^{\circ}$.由折叠的性质,得$EP = CP$,$DE = DC = 4$,$\angle E = \angle C = 90^{\circ}$.因为$\angle B=\angle E$,$\angle BOP=\angle EOF$,$OP = OF$,所以$\triangle BOP\cong\triangle EOF$,所以$BP = EF$,$OB = OE$.设$BP = EF = x$,则$DF = DE - EF = 4 - x$,$EP = CP = BC - BP = 3 - x$,所以$BF = OB + OF = OE + OP = EP = 3 - x$,所以$AF = AB - BF = x + 1$.因为$AD^{2}+AF^{2}=DF^{2}$,所以$3^{2}+(x + 1)^{2}=(4 - x)^{2}$,解得$x=\frac{3}{5}$,所以$DF=\frac{17}{5}$,所以$\cos\angle ADF=\frac{AD}{DF}=\frac{15}{17}$.
15. 如图,在Rt△ABC中,∠B=90°,AB=2$\sqrt{5}$,BC=$\sqrt{5}$.将△ABC绕点A按逆时针方向旋转90°得到△AB'C',连接B'C,则sin∠ACB'=

$\frac{4}{5}$
.
答案:15.$\frac{4}{5}$ 解析:过点$B'$作$B'D⊥ AC$于点D,则$\angle ADB'=\angle CDB' = 90^{\circ}$.因为$\angle B = 90^{\circ}$,$AB = 2\sqrt{5}$,$BC=\sqrt{5}$,所以$CA=\sqrt{AB^{2}+BC^{2}} = 5$.由旋转的性质,得$AB' = AB = 2\sqrt{5}$,$\angle B'AB = 90^{\circ}$,所以$\angle B'AD+\angle BAC = 90^{\circ}$.因为$\angle ACB+\angle BAC = 90^{\circ}$,所以$\angle ACB=\angle B'AD$.又$\angle B=\angle ADB'$,所以$\triangle ABC∼\triangle B'DA$,所以$\frac{BC}{DA}=\frac{CA}{AB'}=\frac{AB}{B'D}$,即$\frac{\sqrt{5}}{DA}=\frac{5}{2\sqrt{5}}=\frac{2\sqrt{5}}{B'D}$,所以$DA = 2$,$B'D = 4$,所以$CD=CA - DA = 3$,所以$B'C=\sqrt{B'D^{2}+CD^{2}} = 5$,所以$\sin\angle ACB'=\frac{B'D}{B'C}=\frac{4}{5}$.
解析:
解:过点$B'$作$B'D ⊥ AC$于点$D$,则$\angle ADB' = \angle CDB' = 90°$。
在$Rt\triangle ABC$中,$\angle B = 90°$,$AB = 2\sqrt{5}$,$BC = \sqrt{5}$,
$\therefore AC = \sqrt{AB^2 + BC^2} = \sqrt{(2\sqrt{5})^2 + (\sqrt{5})^2} = 5$。
由旋转性质得:$AB' = AB = 2\sqrt{5}$,$\angle B'AB = 90°$,
$\therefore \angle B'AD + \angle BAC = 90°$。
$\because \angle ACB + \angle BAC = 90°$,
$\therefore \angle ACB = \angle B'AD$。
又$\angle B = \angle ADB' = 90°$,
$\therefore \triangle ABC ∼ \triangle B'DA$。
$\therefore \frac{BC}{DA} = \frac{CA}{AB'} = \frac{AB}{B'D}$,即$\frac{\sqrt{5}}{DA} = \frac{5}{2\sqrt{5}} = \frac{2\sqrt{5}}{B'D}$,
解得$DA = 2$,$B'D = 4$。
$\therefore CD = AC - DA = 5 - 2 = 3$,
$\therefore B'C = \sqrt{B'D^2 + CD^2} = \sqrt{4^2 + 3^2} = 5$。
$\therefore \sin\angle ACB' = \frac{B'D}{B'C} = \frac{4}{5}$。
$\frac{4}{5}$
在$Rt\triangle ABC$中,$\angle B = 90°$,$AB = 2\sqrt{5}$,$BC = \sqrt{5}$,
$\therefore AC = \sqrt{AB^2 + BC^2} = \sqrt{(2\sqrt{5})^2 + (\sqrt{5})^2} = 5$。
由旋转性质得:$AB' = AB = 2\sqrt{5}$,$\angle B'AB = 90°$,
$\therefore \angle B'AD + \angle BAC = 90°$。
$\because \angle ACB + \angle BAC = 90°$,
$\therefore \angle ACB = \angle B'AD$。
又$\angle B = \angle ADB' = 90°$,
$\therefore \triangle ABC ∼ \triangle B'DA$。
$\therefore \frac{BC}{DA} = \frac{CA}{AB'} = \frac{AB}{B'D}$,即$\frac{\sqrt{5}}{DA} = \frac{5}{2\sqrt{5}} = \frac{2\sqrt{5}}{B'D}$,
解得$DA = 2$,$B'D = 4$。
$\therefore CD = AC - DA = 5 - 2 = 3$,
$\therefore B'C = \sqrt{B'D^2 + CD^2} = \sqrt{4^2 + 3^2} = 5$。
$\therefore \sin\angle ACB' = \frac{B'D}{B'C} = \frac{4}{5}$。
$\frac{4}{5}$
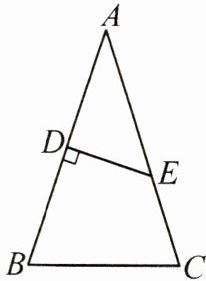
16. 如图,在△ABC中,AB=AC=4,∠C=72°,D是AB的中点,点E在AC上,且DE⊥AB,求cosA的值.

答案:16.连接BE.因为$AB = AC = 4$,所以$\angle ABC=\angle C = 72^{\circ}$,所以$\angle A = 180^{\circ}-\angle ABC-\angle C = 36^{\circ}$.因为D是AB的中点,$DE⊥ AB$,所以$AD=\frac{1}{2}AB = 2$,$\angle ADE = 90^{\circ}$,DE垂直平分AB,所以$AE = BE$,所以$\angle ABE=\angle A = 36^{\circ}$,所以$\angle EBC=\angle ABC-\angle ABE = 36^{\circ}$,所以$\angle BEC = 180^{\circ}-\angle EBC-\angle C = 72^{\circ}$,所以$\angle BEC=\angle C$,所以$BE = BC$,所以$AE = BE = BC$.设$AE = BE = BC = x$,则$EC = AC - AE = 4 - x$.因为$\angle EBC=\angle A$,$\angle BCE=\angle ACB$,所以$\triangle BCE∼\triangle ACB$,所以$\frac{EC}{BC}=\frac{BE}{AB}$,即$\frac{4 - x}{x}=\frac{x}{4}$,解得$x=-2\pm2\sqrt{5}$.经检验,它们都是原分式方程的解.又$0<x<4$,所以$AE=-2 + 2\sqrt{5}$,所以$\cos A=\frac{AD}{AE}=\frac{\sqrt{5}+1}{4}$.
解析:
解:连接BE.
∵AB=AC=4,
∴∠ABC=∠C=72°,
∴∠A=180°-∠ABC-∠C=36°.
∵D是AB的中点,DE⊥AB,
∴AD=1/2AB=2,DE垂直平分AB,
∴AE=BE,
∴∠ABE=∠A=36°,
∴∠EBC=∠ABC-∠ABE=36°,
∴∠BEC=180°-∠EBC-∠C=72°,
∴∠BEC=∠C,
∴BE=BC,
∴AE=BE=BC.
设AE=BE=BC=x,则EC=AC-AE=4-x.
∵∠EBC=∠A,∠BCE=∠ACB,
∴△BCE∼△ACB,
∴EC/BC=BE/AB,即(4-x)/x=x/4,
解得x=-2±2√5.
∵0<x<4,
∴AE=-2+2√5,
∴cosA=AD/AE=2/(-2+2√5)=(√5+1)/4.
∵AB=AC=4,
∴∠ABC=∠C=72°,
∴∠A=180°-∠ABC-∠C=36°.
∵D是AB的中点,DE⊥AB,
∴AD=1/2AB=2,DE垂直平分AB,
∴AE=BE,
∴∠ABE=∠A=36°,
∴∠EBC=∠ABC-∠ABE=36°,
∴∠BEC=180°-∠EBC-∠C=72°,
∴∠BEC=∠C,
∴BE=BC,
∴AE=BE=BC.
设AE=BE=BC=x,则EC=AC-AE=4-x.
∵∠EBC=∠A,∠BCE=∠ACB,
∴△BCE∼△ACB,
∴EC/BC=BE/AB,即(4-x)/x=x/4,
解得x=-2±2√5.
∵0<x<4,
∴AE=-2+2√5,
∴cosA=AD/AE=2/(-2+2√5)=(√5+1)/4.