1. (2025·湖北)如图,甲、乙两栋楼相距 30 m,从甲楼 A 处看乙楼顶部 B 的仰角为 $ 35^{\circ} $,A 处到地面的距离为 18 m,求乙楼的高.(参考数据: $ \tan 35^{\circ} \approx 0.7 $)
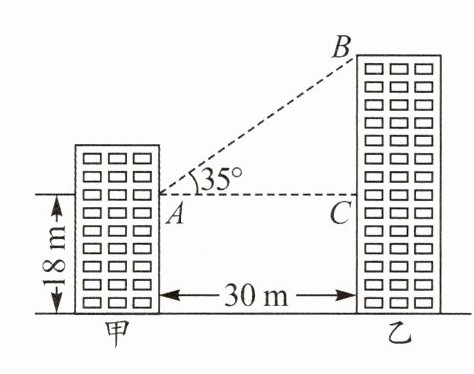

答案:1. 由题意,得$\angle ACB = 90°$,$\angle BAC = 35°$,$AC = 30\mathrm{ m}$,所以$BC=AC·\tan\angle BAC\approx30×0.7 = 21(\mathrm{m})$,所以$21 + 18 = 39(\mathrm{m})$。故乙楼的高为$39\mathrm{ m}$。
解析:
解:过点A作$AC⊥ BD$于点C,由题意得,$AC=30\ \mathrm{m}$,$CD=18\ \mathrm{m}$,$\angle BAC=35°$。
在$Rt\triangle ABC$中,$\tan\angle BAC=\frac{BC}{AC}$,
则$BC=AC·\tan35°\approx30×0.7=21\ \mathrm{m}$。
所以乙楼的高$BD=BC+CD=21+18=39\ \mathrm{m}$。
答:乙楼的高为$39\ \mathrm{m}$。
在$Rt\triangle ABC$中,$\tan\angle BAC=\frac{BC}{AC}$,
则$BC=AC·\tan35°\approx30×0.7=21\ \mathrm{m}$。
所以乙楼的高$BD=BC+CD=21+18=39\ \mathrm{m}$。
答:乙楼的高为$39\ \mathrm{m}$。
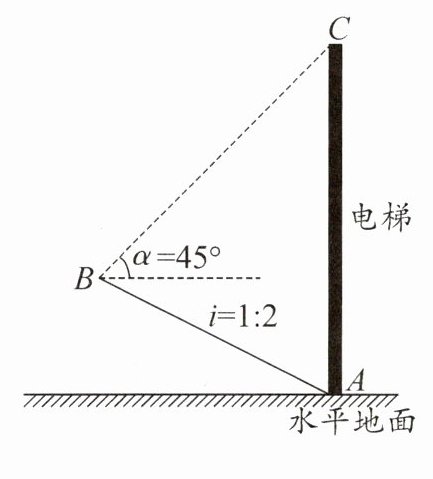
2. 新素养 应用意识 (2025·江苏宿迁模拟)如图,某景区新建了一座垂直观光电梯.某测绘兴趣小组为测算电梯 AC 的高度,测得斜坡 $ AB = 105 \, \mathrm{m} $,坡度 $ i = 1:2 $,在 B 处测得电梯顶端 C 的仰角 $ \alpha = 45^{\circ} $,求观光电梯 AC 的高度.(结果精确到 $ 0.1 \, \mathrm{m} $,参考数据: $ \sqrt{2} \approx 1.41 $, $ \sqrt{3} \approx 1.73 $, $ \sqrt{5} \approx 2.24 $)

答案:
2. 如图,过点$B$分别作$BD⊥ AC$于点$D$,$BE$垂直水平地面于点$E$,则$\angle ADB=\angle CDB=\angle AEB = 90°$。由题意,得$\angle CBD = 45°$,$\frac{BE}{AE}=\frac{1}{2}$,$\angle DAE = 90°$,所以四边形$ADBE$是矩形,所以$BD = AE$,$AD = BE$。设$AD = BE = x\mathrm{ m}$,则$BD = AE = 2x\mathrm{ m}$,所以$AB=\sqrt{BE^2 + AE^2}=\sqrt{5}x\mathrm{ m}$。因为$AB = 105\mathrm{ m}$,所以$\sqrt{5}x = 105$,解得$x = 21\sqrt{5}$,所以$AD = 21\sqrt{5}\mathrm{ m}$,$BD = 42\sqrt{5}\mathrm{ m}$,所以$CD = BD·\tan\angle CBD = 42\sqrt{5}\mathrm{ m}$,所以$AC = AD + CD = 63\sqrt{5}\mathrm{ m}\approx141.1\mathrm{ m}$。故观光电梯$AC$的高度约为$141.1\mathrm{ m}$。

2. 如图,过点$B$分别作$BD⊥ AC$于点$D$,$BE$垂直水平地面于点$E$,则$\angle ADB=\angle CDB=\angle AEB = 90°$。由题意,得$\angle CBD = 45°$,$\frac{BE}{AE}=\frac{1}{2}$,$\angle DAE = 90°$,所以四边形$ADBE$是矩形,所以$BD = AE$,$AD = BE$。设$AD = BE = x\mathrm{ m}$,则$BD = AE = 2x\mathrm{ m}$,所以$AB=\sqrt{BE^2 + AE^2}=\sqrt{5}x\mathrm{ m}$。因为$AB = 105\mathrm{ m}$,所以$\sqrt{5}x = 105$,解得$x = 21\sqrt{5}$,所以$AD = 21\sqrt{5}\mathrm{ m}$,$BD = 42\sqrt{5}\mathrm{ m}$,所以$CD = BD·\tan\angle CBD = 42\sqrt{5}\mathrm{ m}$,所以$AC = AD + CD = 63\sqrt{5}\mathrm{ m}\approx141.1\mathrm{ m}$。故观光电梯$AC$的高度约为$141.1\mathrm{ m}$。

3. 如图,B 港口在 A 港口的南偏西 $ 25^{\circ} $方向上,距离 A 港口 100 海里处,一艘货轮航行到 C 处,发现 A 港口在货轮的北偏西 $ 25^{\circ} $方向上,B 港口在货轮的北偏西 $ 70^{\circ} $方向上.求此时货轮与 A 港口的距离.(结果取整数,参考数据: $ \sin 50^{\circ} \approx 0.766 $, $ \cos 50^{\circ} \approx 0.643 $, $ \tan 50^{\circ} \approx 1.192 $, $ \sqrt{2} \approx 1.414 $)
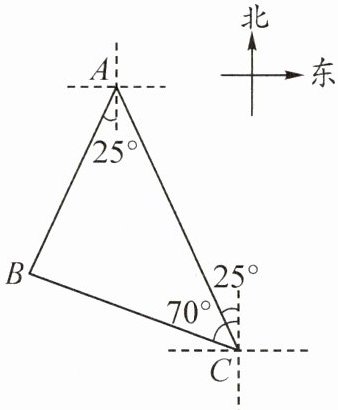

答案:3. 过点$B$作$BD⊥ AC$于点$D$,则$\angle ADB=\angle CDB = 90°$。由题意,得$AB = 100$海里,$\angle BAC = 25°+25° = 50°$,$\angle BCA = 70°-25° = 45°$,所以$AD = AB·\cos\angle BAC\approx100×0.643 = 64.3$(海里),$BD = AB·\sin\angle BAC\approx100×0.766 = 76.6$(海里),所以$CD=\frac{BD}{\tan\angle BCA}=76.6$海里,所以$AC = AD + CD = 140.9$海里$\approx141$海里。故此时货轮与$A$港口的距离约为$141$海里。
解析:
过点$B$作$BD⊥ AC$于点$D$,则$\angle ADB = \angle CDB=90°$。
由题意得:$AB = 100$海里,$\angle BAC=25° + 25°=50°$,$\angle BCA=70° - 25°=45°$。
在$\mathrm{Rt}\triangle ABD$中,$AD=AB·\cos\angle BAC\approx100×0.643 = 64.3$海里,$BD=AB·\sin\angle BAC\approx100×0.766 = 76.6$海里。
在$\mathrm{Rt}\triangle CBD$中,$CD=\frac{BD}{\tan\angle BCA}=\frac{76.6}{\tan45°}=76.6$海里。
$AC=AD + CD=64.3 + 76.6=140.9\approx141$海里。
故此时货轮与$A$港口的距离约为$141$海里。
由题意得:$AB = 100$海里,$\angle BAC=25° + 25°=50°$,$\angle BCA=70° - 25°=45°$。
在$\mathrm{Rt}\triangle ABD$中,$AD=AB·\cos\angle BAC\approx100×0.643 = 64.3$海里,$BD=AB·\sin\angle BAC\approx100×0.766 = 76.6$海里。
在$\mathrm{Rt}\triangle CBD$中,$CD=\frac{BD}{\tan\angle BCA}=\frac{76.6}{\tan45°}=76.6$海里。
$AC=AD + CD=64.3 + 76.6=140.9\approx141$海里。
故此时货轮与$A$港口的距离约为$141$海里。
4. (2024·四川泸州)如图,海中有一个小岛 C,某渔船在海中的 A 处测得小岛 C 位于东北方向上,该渔船由西向东航行一段时间后到达 B 处,测得小岛 C 位于北偏西 $ 30^{\circ} $方向上,再沿北偏东 $ 60^{\circ} $方向继续航行一段时间后到达 D 处,这时测得小岛 C 位于北偏西 $ 60^{\circ} $方向上.已知 A,C 相距 30 n mile.求 C,D 之间的距离.
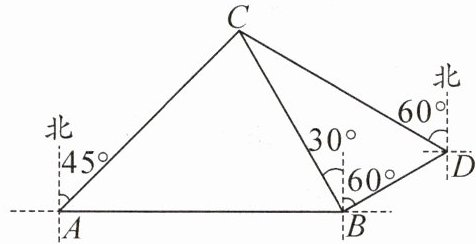

答案:4. 过点$C$作$CE⊥ AB$于点$E$,则$\angle AEC=\angle BEC = 90°$。因为$AC = 30\mathrm{ n mile}$,$\angle ACE = 45°$,所以$CE = AC·\cos\angle ACE = 15\sqrt{2}\mathrm{ n mile}$。因为$\angle BCE = 30°$,所以$BC=\frac{CE}{\cos\angle BCE}=10\sqrt{6}\mathrm{ n mile}$。因为$\angle DCE = 60°$,所以$\angle BCD=\angle DCE-\angle BCE = 30°$。因为$\angle CBD = 30°+60° = 90°$,所以$CD=\frac{BC}{\cos\angle BCD}=20\sqrt{2}\mathrm{ n mile}$。故$C$,$D$之间的距离为$20\sqrt{2}\mathrm{ n mile}$。
解析:
解:过点$C$作$CE ⊥ AB$于点$E$,则$\angle AEC = \angle BEC = 90°$。
在$Rt\triangle AEC$中,$AC = 30$ n mile,$\angle ACE = 45°$,
$CE = AC · \cos\angle ACE = 30 · \cos45° = 30 · \frac{\sqrt{2}}{2} = 15\sqrt{2}$ n mile。
在$Rt\triangle BEC$中,$\angle BCE = 30°$,
$BC = \frac{CE}{\cos\angle BCE} = \frac{15\sqrt{2}}{\cos30°} = \frac{15\sqrt{2}}{\frac{\sqrt{3}}{2}} = 10\sqrt{6}$ n mile。
由题意得$\angle DCE = 60°$,$\angle CBD = 30° + 60° = 90°$,
$\angle BCD = \angle DCE - \angle BCE = 60° - 30° = 30°$。
在$Rt\triangle BCD$中,
$CD = \frac{BC}{\cos\angle BCD} = \frac{10\sqrt{6}}{\cos30°} = \frac{10\sqrt{6}}{\frac{\sqrt{3}}{2}} = 20\sqrt{2}$ n mile。
故$C$,$D$之间的距离为$20\sqrt{2}$ n mile。
在$Rt\triangle AEC$中,$AC = 30$ n mile,$\angle ACE = 45°$,
$CE = AC · \cos\angle ACE = 30 · \cos45° = 30 · \frac{\sqrt{2}}{2} = 15\sqrt{2}$ n mile。
在$Rt\triangle BEC$中,$\angle BCE = 30°$,
$BC = \frac{CE}{\cos\angle BCE} = \frac{15\sqrt{2}}{\cos30°} = \frac{15\sqrt{2}}{\frac{\sqrt{3}}{2}} = 10\sqrt{6}$ n mile。
由题意得$\angle DCE = 60°$,$\angle CBD = 30° + 60° = 90°$,
$\angle BCD = \angle DCE - \angle BCE = 60° - 30° = 30°$。
在$Rt\triangle BCD$中,
$CD = \frac{BC}{\cos\angle BCD} = \frac{10\sqrt{6}}{\cos30°} = \frac{10\sqrt{6}}{\frac{\sqrt{3}}{2}} = 20\sqrt{2}$ n mile。
故$C$,$D$之间的距离为$20\sqrt{2}$ n mile。
5. 如图,无人机在离地面 60 m 的 C 处,观测楼房顶部 B 的俯角为 $ 30^{\circ} $,观测楼房底部 A 的俯角为 $ 60^{\circ} $,求楼房的高度.
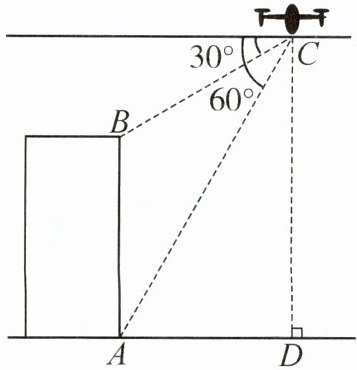

答案:5. 过点$B$作$BE⊥ CD$于点$E$,则$\angle BEC=\angle BED = 90°$。由题意,得$CD = 60\mathrm{ m}$,$\angle CAD = 60°$,$\angle CBE = 30°$,$\angle BAD=\angle ADC = 90°$,所以四边形$ABED$是矩形,所以$AB = DE$,$BE = AD=\frac{CD}{\tan\angle CAD}=20\sqrt{3}\mathrm{ m}$,所以$CE = BE·\tan\angle CBE = 20\mathrm{ m}$,所以$AB = DE = CD - CE = 40\mathrm{ m}$。故楼房的高度为$40\mathrm{ m}$。
解析:
解:过点$B$作$BE ⊥ CD$于点$E$,则$\angle BEC = 90°$。
由题意得:$CD = 60\ \mathrm{m}$,$\angle CAD = 60°$,$\angle CBE = 30°$,$\angle BAD = \angle ADC = 90°$,
$\therefore$四边形$ABED$是矩形,$\therefore AB = DE$,$BE = AD$。
在$\mathrm{Rt}\triangle ACD$中,$AD=\frac{CD}{\tan\angle CAD}=\frac{60}{\tan60°}=\frac{60}{\sqrt{3}}=20\sqrt{3}\ \mathrm{m}$,$\therefore BE = 20\sqrt{3}\ \mathrm{m}$。
在$\mathrm{Rt}\triangle BCE$中,$CE=BE·\tan\angle CBE=20\sqrt{3}·\tan30°=20\sqrt{3}·\frac{\sqrt{3}}{3}=20\ \mathrm{m}$。
$\therefore AB=DE=CD - CE=60 - 20=40\ \mathrm{m}$。
故楼房的高度为$40\ \mathrm{m}$。
由题意得:$CD = 60\ \mathrm{m}$,$\angle CAD = 60°$,$\angle CBE = 30°$,$\angle BAD = \angle ADC = 90°$,
$\therefore$四边形$ABED$是矩形,$\therefore AB = DE$,$BE = AD$。
在$\mathrm{Rt}\triangle ACD$中,$AD=\frac{CD}{\tan\angle CAD}=\frac{60}{\tan60°}=\frac{60}{\sqrt{3}}=20\sqrt{3}\ \mathrm{m}$,$\therefore BE = 20\sqrt{3}\ \mathrm{m}$。
在$\mathrm{Rt}\triangle BCE$中,$CE=BE·\tan\angle CBE=20\sqrt{3}·\tan30°=20\sqrt{3}·\frac{\sqrt{3}}{3}=20\ \mathrm{m}$。
$\therefore AB=DE=CD - CE=60 - 20=40\ \mathrm{m}$。
故楼房的高度为$40\ \mathrm{m}$。