17. (2025·江苏苏州模拟)已知二次函数$y = ax^{2}-3ax + 3$的图像经过点$A(6,0)$,且与$y$轴交于点$B$,点$M$在该抛物线的对称轴上.若$\triangle ABM$是以$AB$为直角边的直角三角形,则点$M$的坐标为
$(\frac{3}{2},6)$或$(\frac{3}{2},-9)$
.答案:17.$(\frac{3}{2},6)$或$(\frac{3}{2},-9)$ 解析:在$y=ax^{2}-3ax + 3$中,令$x=0$,得$y=3$,所以$B(0,3)$.因为抛物线$y=ax^{2}-3ax + 3$的对称轴为直线$x=\frac{-(-3a)}{2a}=\frac{3}{2}$,所以可设点$M$的坐标为$(\frac{3}{2},m)$.又$A(6,0)$,所以$AB^{2}=(6 - 0)^{2}+(0 - 3)^{2}=45$,$AM^{2}=(6 - \frac{3}{2})^{2}+(0 - m)^{2}=m^{2}+\frac{81}{4}$,$BM^{2}=(0 - \frac{3}{2})^{2}+(3 - m)^{2}=m^{2}-6m+\frac{45}{4}$.当$\triangle ABM$是以$AB$为直角边的直角三角形时,分类讨论如下:
①若$\angle ABM = 90^{\circ}$,则$AB^{2}+BM^{2}=AM^{2}$,即$45 + m^{2}-6m+\frac{45}{4}=m^{2}+\frac{81}{4}$,解得$m = 6$,所以$M(\frac{3}{2},6)$;
②若$\angle BAM = 90^{\circ}$,则$AB^{2}+AM^{2}=BM^{2}$,即$45 + m^{2}+\frac{81}{4}=m^{2}-6m+\frac{45}{4}$,解得$m = - 9$,所以$M(\frac{3}{2},-9)$.
综上所述,点$M$的坐标为$(\frac{3}{2},6)$或$(\frac{3}{2},-9)$.
①若$\angle ABM = 90^{\circ}$,则$AB^{2}+BM^{2}=AM^{2}$,即$45 + m^{2}-6m+\frac{45}{4}=m^{2}+\frac{81}{4}$,解得$m = 6$,所以$M(\frac{3}{2},6)$;
②若$\angle BAM = 90^{\circ}$,则$AB^{2}+AM^{2}=BM^{2}$,即$45 + m^{2}+\frac{81}{4}=m^{2}-6m+\frac{45}{4}$,解得$m = - 9$,所以$M(\frac{3}{2},-9)$.
综上所述,点$M$的坐标为$(\frac{3}{2},6)$或$(\frac{3}{2},-9)$.
18. 在平面直角坐标系中,已知点$C$和点$D$的坐标分别为$(-1,-1)$和$(4,-1)$,抛物线$y = mx^{2}-2mx + 2$与线段$CD$只有一个交点,则实数$m$的取值范围是
$m = 3$或$-1<m\leq-\frac{3}{8}$
.答案:18.$m = 3$或$-1<m\leq-\frac{3}{8}$ 解析:因为$y=mx^{2}-2mx + 2=m(x^{2}-2x)+2=m(x - 1)^{2}+2 - m$,所以该抛物线的顶点坐标为$(1,2 - m)$,且经过点$(0,2)$和点$(2,2)$.因为该抛物线与线段$CD$只有一个交点,所以分类讨论如下:
①当点$(1,2 - m)$在线段$CD$上时,$2 - m=-1$,解得$m = 3$,符合题意;
②当点$(1,2 - m)$不在线段$CD$上时,$m<0$.设该抛物线与线段$CD$的唯一交点为$(t,-1)$,则该抛物线与直线$CD$的另一个交点为$(2 - t,-1)$,所以$2 - t>4$或$2 - t<-1$,所以$t<-2$或$t>3$.又$-1\leq t\leq4$,所以$3<t\leq4$.在$y=mx^{2}-2mx + 2$中,令$x = 3$,得$y = 9m-6m + 2=3m + 2$;令$x = 4$,得$y = 16m-8m + 2=8m + 2$.由题意,得$\begin{cases}3m + 2>-1\\8m + 2\leq-1\end{cases}$,解得$-1<m\leq-\frac{3}{8}$.
综上所述,当抛物线$y=mx^{2}-2mx + 2$与线段$CD$只有一个交点时,实数$m$的取值范围是$m = 3$或$-1<m\leq-\frac{3}{8}$.
①当点$(1,2 - m)$在线段$CD$上时,$2 - m=-1$,解得$m = 3$,符合题意;
②当点$(1,2 - m)$不在线段$CD$上时,$m<0$.设该抛物线与线段$CD$的唯一交点为$(t,-1)$,则该抛物线与直线$CD$的另一个交点为$(2 - t,-1)$,所以$2 - t>4$或$2 - t<-1$,所以$t<-2$或$t>3$.又$-1\leq t\leq4$,所以$3<t\leq4$.在$y=mx^{2}-2mx + 2$中,令$x = 3$,得$y = 9m-6m + 2=3m + 2$;令$x = 4$,得$y = 16m-8m + 2=8m + 2$.由题意,得$\begin{cases}3m + 2>-1\\8m + 2\leq-1\end{cases}$,解得$-1<m\leq-\frac{3}{8}$.
综上所述,当抛物线$y=mx^{2}-2mx + 2$与线段$CD$只有一个交点时,实数$m$的取值范围是$m = 3$或$-1<m\leq-\frac{3}{8}$.
19. (6分)已知抛物线$y = a(x - 1)^{2}+h$经过点$(0,-3)$和$(3,0)$.
(1) 求$a$,$h$的值;
(2) 将该抛物线先向上平移$2$个单位长度,再向右平移$1$个单位长度,得到新的抛物线,直接写出新抛物线的函数表达式.
(1) 求$a$,$h$的值;
(2) 将该抛物线先向上平移$2$个单位长度,再向右平移$1$个单位长度,得到新的抛物线,直接写出新抛物线的函数表达式.
答案:19.(1)因为抛物线$y=a(x - 1)^{2}+h$经过点$(0,-3)$和$(3,0)$,所以$\begin{cases}a + h=-3\\4a + h=0\end{cases}$,解得$\begin{cases}a = 1\\h=-4\end{cases}$.
(2)由(1),得原抛物线的函数表达式为$y=(x - 1)^{2}-4$,则新抛物线的函数表达式为$y=(x - 2)^{2}-2$,即$y=x^{2}-4x + 2$.
(2)由(1),得原抛物线的函数表达式为$y=(x - 1)^{2}-4$,则新抛物线的函数表达式为$y=(x - 2)^{2}-2$,即$y=x^{2}-4x + 2$.
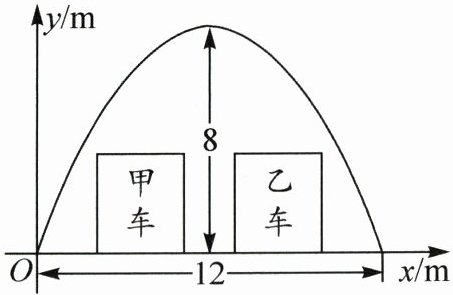
20. (8分)(2025·新疆)天山胜利隧道于2025年建成通车,它成为世界上最长的高速公路隧道,能大大提升区域交通效率,促进经济发展.如图是隧道截面图,其轮廓可近似看作是抛物线的一部分.已知隧道的底部宽$12m$,高$8m$,按照如图所示的方式建立平面直角坐标系.
(1) 求该抛物线的函数表达式;
(2) 该隧道设计为单向双车道通行,车辆顶部在竖直方向上与隧道的空隙不少于$0.5m$,当两辆车在隧道内并排行驶时,需沿中心线两侧行驶,且两车至少间隔$2m$(中心线宽度忽略不计).若宽$3m$,高$3.5m$的两辆车并排行驶,则能否安全通过?请说明理由.
(1) 求该抛物线的函数表达式;
(2) 该隧道设计为单向双车道通行,车辆顶部在竖直方向上与隧道的空隙不少于$0.5m$,当两辆车在隧道内并排行驶时,需沿中心线两侧行驶,且两车至少间隔$2m$(中心线宽度忽略不计).若宽$3m$,高$3.5m$的两辆车并排行驶,则能否安全通过?请说明理由.

答案:20.(1)由题意,得该抛物线顶点的横坐标为$\frac{1}{2}×12 = 6$,纵坐标为$8$,所以可设该抛物线的函数表达式为$y=a(x - 6)^{2}+8$.把点$(12,0)$代入$y=a(x - 6)^{2}+8$,得$36a + 8=0$,解得$a=-\frac{2}{9}$,所以$y=-\frac{2}{9}(x - 6)^{2}+8=-\frac{2}{9}x^{2}+\frac{8}{3}x$.故该抛物线的函数表达式为$y=-\frac{2}{9}x^{2}+\frac{8}{3}x(0\leq x\leq12)$.
(2)能安全通过.理由如下:在$y=-\frac{2}{9}x^{2}+\frac{8}{3}x$中,当$x=6-(3+\frac{1}{2}×2)=2$时,$y=-\frac{2}{9}×4+\frac{8}{3}×2=\frac{40}{9}$,所以$\frac{40}{9}-3.5=\frac{17}{18}(m)$.因为$\frac{17}{18}>0.5$,所以能安全通过.
(2)能安全通过.理由如下:在$y=-\frac{2}{9}x^{2}+\frac{8}{3}x$中,当$x=6-(3+\frac{1}{2}×2)=2$时,$y=-\frac{2}{9}×4+\frac{8}{3}×2=\frac{40}{9}$,所以$\frac{40}{9}-3.5=\frac{17}{18}(m)$.因为$\frac{17}{18}>0.5$,所以能安全通过.
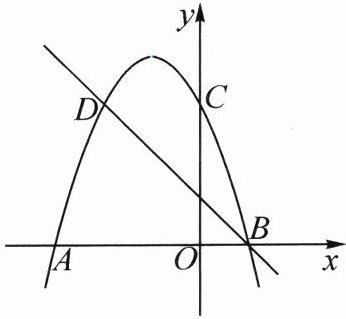
21. (8分)(2025·江苏无锡模拟)如图,二次函数的图像与$x$轴交于$A(-3,0)$,$B(1,0)$两点,与$y$轴交于点$C(0,3)$,$C$,$D$是该二次函数图像上的一对对称点,一次函数的图像经过点$B$,$D$.
(1) 请直接写出点$D$的坐标;
(2) 求该二次函数的表达式;
(3) 根据图像直接写出使一次函数值大于二次函数值的$x$的取值范围.
(1) 请直接写出点$D$的坐标;
(2) 求该二次函数的表达式;
(3) 根据图像直接写出使一次函数值大于二次函数值的$x$的取值范围.

答案:21.(1)因为二次函数的图像与$x$轴交于$A(-3,0)$,$B(1,0)$两点,所以该二次函数的图像的对称轴为直线$x=-1$.因为$C(0,3)$,$D$是该二次函数图像上的一对对称点,所以点$D$的坐标为$(-2,3)$.
(2)设该二次函数的表达式为$y=a(x + 3)(x - 1)$.把点$C(0,3)$代入$y=a(x + 3)(x - 1)$,得$-3a = 3$,解得$a=-1$,所以该二次函数的表达式为$y=-(x + 3)(x - 1)=-x^{2}-2x + 3$.
(3)观察题图可知,当$x<-2$或$x>1$时,一次函数的图像在二次函数的图像的上方,所以使一次函数值大于二次函数值的$x$的取值范围为$x<-2$或$x>1$.
(2)设该二次函数的表达式为$y=a(x + 3)(x - 1)$.把点$C(0,3)$代入$y=a(x + 3)(x - 1)$,得$-3a = 3$,解得$a=-1$,所以该二次函数的表达式为$y=-(x + 3)(x - 1)=-x^{2}-2x + 3$.
(3)观察题图可知,当$x<-2$或$x>1$时,一次函数的图像在二次函数的图像的上方,所以使一次函数值大于二次函数值的$x$的取值范围为$x<-2$或$x>1$.