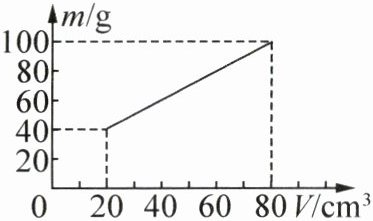
7. (2025·江苏南京期末)为测量某种液体的密度,小明利用天平和量杯测量了液体和量杯的总质量m及液体的体积V,得到几组数据并绘制出了m-V图像,如图所示。下列说法正确的是(
A.量杯质量为40g
B.该液体密度为2g/cm³
C.该液体密度为1g/cm³
D.80cm³的该液体质量为60g
C
)
A.量杯质量为40g
B.该液体密度为2g/cm³
C.该液体密度为1g/cm³
D.80cm³的该液体质量为60g
答案:7.C
解析:
解:设量杯质量为$m_0$,液体密度为$\rho$。
由图像知,当$V_1=20\,\mathrm{cm}^3$时,$m_1=40\,\mathrm{g}$,则$m_1 = m_0+\rho V_1$,即$40 = m_0+20\rho$;
当$V_2=80\,\mathrm{cm}^3$时,$m_2=100\,\mathrm{g}$,则$m_2 = m_0+\rho V_2$,即$100 = m_0+80\rho$。
联立方程:$\begin{cases}m_0 + 20\rho=40\\m_0 + 80\rho=100\end{cases}$
两式相减得:$60\rho=60$,解得$\rho = 1\,\mathrm{g/cm}^3$。
将$\rho=1\,\mathrm{g/cm}^3$代入$40 = m_0+20×1$,得$m_0=20\,\mathrm{g}$。
当$V=80\,\mathrm{cm}^3$时,液体质量$m=\rho V=1\,\mathrm{g/cm}^3×80\,\mathrm{cm}^3 = 80\,\mathrm{g}$。
综上,正确的是C。
C
由图像知,当$V_1=20\,\mathrm{cm}^3$时,$m_1=40\,\mathrm{g}$,则$m_1 = m_0+\rho V_1$,即$40 = m_0+20\rho$;
当$V_2=80\,\mathrm{cm}^3$时,$m_2=100\,\mathrm{g}$,则$m_2 = m_0+\rho V_2$,即$100 = m_0+80\rho$。
联立方程:$\begin{cases}m_0 + 20\rho=40\\m_0 + 80\rho=100\end{cases}$
两式相减得:$60\rho=60$,解得$\rho = 1\,\mathrm{g/cm}^3$。
将$\rho=1\,\mathrm{g/cm}^3$代入$40 = m_0+20×1$,得$m_0=20\,\mathrm{g}$。
当$V=80\,\mathrm{cm}^3$时,液体质量$m=\rho V=1\,\mathrm{g/cm}^3×80\,\mathrm{cm}^3 = 80\,\mathrm{g}$。
综上,正确的是C。
C
8. 小向同学陪妈妈去超市买厨房用品,他发现超市中同一品牌、同一种类的酱油,有两种规格:第一种是袋装450毫升,售价5元;第二种是瓶装500克,售价6元。已知袋装酱油的密度为1.2克/毫升。以下说法正确的是(
A.两种包装的酱油质量相同,袋装酱油更便宜
B.两种包装的酱油质量不同,瓶装酱油更便宜
C.两种包装的酱油密度相同,袋装酱油更便宜
D.两种包装的酱油密度不同,瓶装酱油更便宜
C
)A.两种包装的酱油质量相同,袋装酱油更便宜
B.两种包装的酱油质量不同,瓶装酱油更便宜
C.两种包装的酱油密度相同,袋装酱油更便宜
D.两种包装的酱油密度不同,瓶装酱油更便宜
答案:8.C
解析:
同一品牌、同一种类的酱油,密度相同。
袋装酱油体积$V_1 = 450$毫升,密度$\rho = 1.2$克/毫升,质量$m_1=\rho V_1=1.2×450 = 540$克,售价5元。
瓶装酱油质量$m_2 = 500$克,售价6元。
袋装酱油单价$\frac{5}{540}\approx0.0093$元/克,瓶装酱油单价$\frac{6}{500}=0.012$元/克,袋装更便宜。
结论:两种包装的酱油密度相同,袋装酱油更便宜。
C
袋装酱油体积$V_1 = 450$毫升,密度$\rho = 1.2$克/毫升,质量$m_1=\rho V_1=1.2×450 = 540$克,售价5元。
瓶装酱油质量$m_2 = 500$克,售价6元。
袋装酱油单价$\frac{5}{540}\approx0.0093$元/克,瓶装酱油单价$\frac{6}{500}=0.012$元/克,袋装更便宜。
结论:两种包装的酱油密度相同,袋装酱油更便宜。
C
9. (2025·江苏苏州月考)如图所示,“嫦娥五号”在月球上收集了一满罐的月球土壤(简称“月壤”)返回地球,科研人员称出其质量为1731g,与计划的2000g存在差距,主要原因是收集罐的容积是按照月壤密度为1.6×10³kg/m³设计的。以下说法正确的是(
A.月壤从月球带回地球后质量变小了
B.月壤的实际密度为1.3848g/cm³
C.收集罐的容积为1081.875cm³
D.要取回2000g月壤,则收集罐的体积应设计为1250cm³
B
)A.月壤从月球带回地球后质量变小了
B.月壤的实际密度为1.3848g/cm³
C.收集罐的容积为1081.875cm³
D.要取回2000g月壤,则收集罐的体积应设计为1250cm³
答案:9.B
解析:
A. 质量是物体的固有属性,不随位置变化,月壤从月球带回地球后质量不变,A错误。
B. 设计密度$\rho_设 = 1.6×10^3\ \mathrm{kg/m}^3 = 1.6\ \mathrm{g/cm}^3$,设计质量$m_设 = 2000\ \mathrm{g}$,收集罐容积$V = \frac{m_设}{\rho_设} = \frac{2000\ \mathrm{g}}{1.6\ \mathrm{g/cm}^3} = 1250\ \mathrm{cm}^3$。实际质量$m_实 = 1731\ \mathrm{g}$,实际密度$\rho_实 = \frac{m_实}{V} = \frac{1731\ \mathrm{g}}{1250\ \mathrm{cm}^3} = 1.3848\ \mathrm{g/cm}^3$,B正确。
C. 由B知收集罐容积为$1250\ \mathrm{cm}^3$,C错误。
D. 要取回$2000\ \mathrm{g}$月壤,收集罐体积应设计为$1250\ \mathrm{cm}^3$,但实际月壤密度小于设计值,此体积无法收集到$2000\ \mathrm{g}$,D错误。
答案:B
B. 设计密度$\rho_设 = 1.6×10^3\ \mathrm{kg/m}^3 = 1.6\ \mathrm{g/cm}^3$,设计质量$m_设 = 2000\ \mathrm{g}$,收集罐容积$V = \frac{m_设}{\rho_设} = \frac{2000\ \mathrm{g}}{1.6\ \mathrm{g/cm}^3} = 1250\ \mathrm{cm}^3$。实际质量$m_实 = 1731\ \mathrm{g}$,实际密度$\rho_实 = \frac{m_实}{V} = \frac{1731\ \mathrm{g}}{1250\ \mathrm{cm}^3} = 1.3848\ \mathrm{g/cm}^3$,B正确。
C. 由B知收集罐容积为$1250\ \mathrm{cm}^3$,C错误。
D. 要取回$2000\ \mathrm{g}$月壤,收集罐体积应设计为$1250\ \mathrm{cm}^3$,但实际月壤密度小于设计值,此体积无法收集到$2000\ \mathrm{g}$,D错误。
答案:B
10. (2025·江苏无锡期末)医用酒精是用水与纯酒精按一定比例混合制成,一般用体积分数$\varphi$表示浓度。体积分数$\varphi$为75%的医用酒精表示纯酒精的体积占医用酒精总体积的75%。当体积分数$\varphi$改变时,混合物密度$\rho$也会随之改变。($\rho_{酒精} = 0.8g/cm^{3}$,$\rho_{水} = 1.0g/cm^{3}$)下列关于$\rho$与$\varphi$的关系图像正确的是(
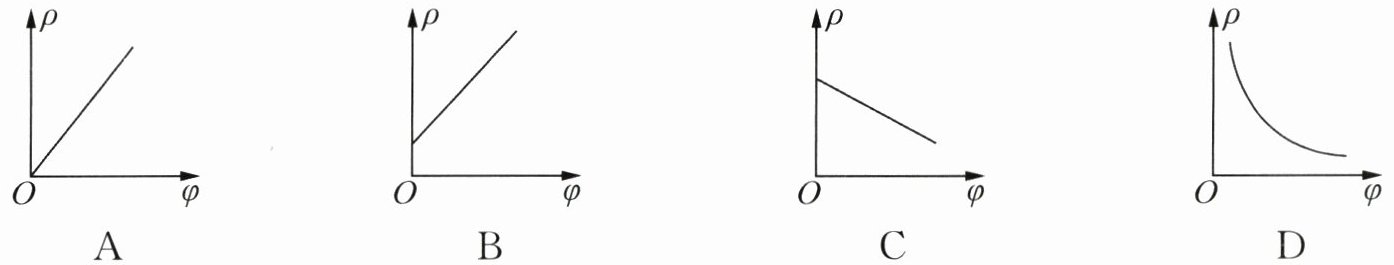
C
)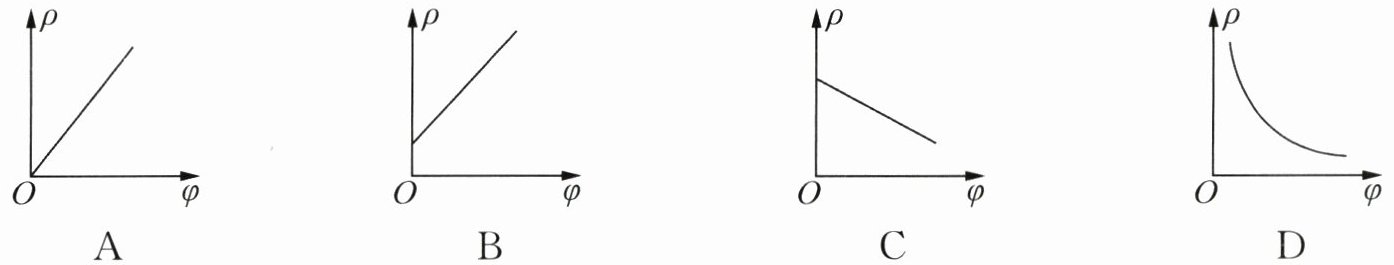
答案:10.C
解析:
设医用酒精总体积为$V$,则纯酒精体积$V_{酒精}=\varphi V$,水的体积$V_{水}=(1 - \varphi)V$。
纯酒精质量$m_{酒精}=\rho_{酒精}V_{酒精}=0.8\varphi V$,水的质量$m_{水}=\rho_{水}V_{水}=1.0(1 - \varphi)V$。
混合物总质量$m = m_{酒精}+m_{水}=0.8\varphi V + 1.0(1 - \varphi)V=(1 - 0.2\varphi)V$。
混合物密度$\rho=\frac{m}{V}=1 - 0.2\varphi$。
$\rho$与$\varphi$成一次函数关系,且斜率为$-0.2$(负斜率),当$\varphi = 0$时,$\rho = 1.0g/cm^{3}$;当$\varphi = 1$时,$\rho = 0.8g/cm^{3}$。图像为过点$(0,1.0)$和$(1,0.8)$的直线,符合选项C。
C
纯酒精质量$m_{酒精}=\rho_{酒精}V_{酒精}=0.8\varphi V$,水的质量$m_{水}=\rho_{水}V_{水}=1.0(1 - \varphi)V$。
混合物总质量$m = m_{酒精}+m_{水}=0.8\varphi V + 1.0(1 - \varphi)V=(1 - 0.2\varphi)V$。
混合物密度$\rho=\frac{m}{V}=1 - 0.2\varphi$。
$\rho$与$\varphi$成一次函数关系,且斜率为$-0.2$(负斜率),当$\varphi = 0$时,$\rho = 1.0g/cm^{3}$;当$\varphi = 1$时,$\rho = 0.8g/cm^{3}$。图像为过点$(0,1.0)$和$(1,0.8)$的直线,符合选项C。
C
11. (2025·陕西西安期中)为了判断一个铜球是否空心,小华进行了如下实验:用调好的天平测量出一个空烧杯的质量为25g,然后将铜球放入烧杯中,测量出烧杯和铜球的总质量为114g,接着往烧杯中加水至铜球被浸没,并在水面处做标记,测量出烧杯、水和铜球的总质量为180g,最后取出铜球并往烧杯中加水至标记处,测量出烧杯和水的总质量为111g。($\rho_{铜} = 8.9×10^{3}kg/m^{3}$,$\rho_{水} = 1.0×10^{3}kg/m^{3}$)下列说法正确的是(
A.铜球是实心的
B.铜球的质量为49g
C.铜球空心部分的体积为10cm³
D.制作铜球时,铜球的体积越大,密度越大
C
)A.铜球是实心的
B.铜球的质量为49g
C.铜球空心部分的体积为10cm³
D.制作铜球时,铜球的体积越大,密度越大
答案:11.C 解析:铜球的质量$m_{铜}=114g - 25g = 89g$,第一次加入水的质量$m_1 = 180g - 114g = 66g$,取出铜球后,加入水的质量$m_2 = 111g - 25g - 66g = 20g$,加入水的体积即铜球的体积$V = \frac{m}{\rho}=\frac{20g}{1g/cm^3}=20cm^3$,铜球中铜的体积$V_{铜}=\frac{m_{铜}}{\rho_{铜}}=\frac{89g}{8.9g/cm^3}=10cm^3$,铜球空心部分的体积$V_{空}=V - V_{铜}=20cm^3 - 10cm^3 = 10cm^3$,故A、B错误,C正确;制作铜球时,铜的质量一定,铜球的体积越大,密度越小,故D错误.