6. (2025·广东二模·2分)如图所示,若在一个圆柱形容器内装满某种液态物质,待其凝固后,容器圆心所在的截面如图乙;取1cm³固态的该物质,质量为m₁,取1cm³液态的该物质,质量为m₂,则有 (

A.m₁>m₂
B.m₁=m₂
C.m₁<m₂
D.条件不足,无法判断m₁和m₂的大小关系
A
)
A.m₁>m₂
B.m₁=m₂
C.m₁<m₂
D.条件不足,无法判断m₁和m₂的大小关系
答案:6. A
7. (2分)小李同学踏青时,带回一杯汾河水,他想测量其密度。他用质量相同的塑料瓶装了体积均为20mL的汾河水和纯净水,分别放在调平的天平的左、右盘上,天平平衡时的状态如图所示,已知ρ₍纯净水₎=1g/cm³,则下列说法正确的是 (
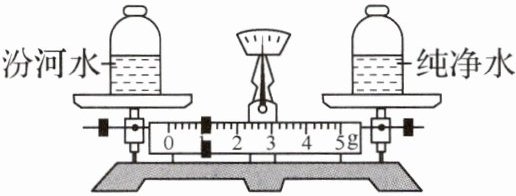
A.瓶和纯净水的总质量为20g
B.汾河水的质量为20g
C.汾河水的密度为1.05g/cm³
D.汾河水的密度为1.1g/cm³
C
)
A.瓶和纯净水的总质量为20g
B.汾河水的质量为20g
C.汾河水的密度为1.05g/cm³
D.汾河水的密度为1.1g/cm³
答案:7. C 解析:已知汾河水和纯净水的体积均为$V = 20 \mathrm{ mL} = 20 \mathrm{ cm}^3$,$\rho_{\mathrm{纯净水}} = 1 \mathrm{ g/cm}^3$,由$\rho = \frac{m}{V}$可得,纯净水的质量$m_{\mathrm{纯净水}} = \rho_{\mathrm{纯净水}} V = 1 \mathrm{ g/cm}^3 × 20 \mathrm{ cm}^3 = 20 \mathrm{ g}$,则瓶和纯净水的总质量大于$20 \mathrm{ g}$,故A错误;由图可知,游码对应刻度为$1 \mathrm{ g}$,天平平衡,则汾河水的质量$m_{\mathrm{汾河水}} = m_{\mathrm{纯净水}} + 1 \mathrm{ g} = 20 \mathrm{ g} + 1 \mathrm{ g} = 21 \mathrm{ g}$,汾河水的密度$\rho_{\mathrm{汾河水}} = \frac{m_{\mathrm{汾河水}}}{V} = \frac{21 \mathrm{ g}}{20 \mathrm{ cm}^3} = 1.05 \mathrm{ g/cm}^3$,故C正确,B、D错误.
8. (2025·江苏常州期中·3分)上分点三 一只新氧气瓶的总质量为55kg,此时瓶内氧气的密度为ρ₀;使用半小时,氧气瓶的总质量变为30kg,瓶内氧气的密度为$\frac{1}{2}ρ₀;$再使用一段时间,氧气瓶的总质量变为15kg,此时瓶内剩余的氧气密度为 (
$A. \frac{1}{3}ρ₀$
$B. \frac{1}{4}ρ₀$
$C. \frac{1}{5}ρ₀$
$D. \frac{1}{6}ρ₀$
C
)$A. \frac{1}{3}ρ₀$
$B. \frac{1}{4}ρ₀$
$C. \frac{1}{5}ρ₀$
$D. \frac{1}{6}ρ₀$
答案:8. C 解析:设氧气瓶的质量为$m_{\mathrm{瓶}}$,容积为$V$,由$\rho = \frac{m}{V}$可得,新氧气瓶内氧气的密度为$\rho_0 = \frac{m_{\mathrm{氧1}}}{V} = \frac{55 \mathrm{ kg} - m_{\mathrm{瓶}}}{V}$ ①;使用半小时后,氧气瓶中氧气的密度为$\frac{1}{2}\rho_0 = \frac{m_{\mathrm{氧2}}}{V} = \frac{30 \mathrm{ kg} - m_{\mathrm{瓶}}}{V}$ ②;由①②式解得$m_{\mathrm{瓶}} = 5 \mathrm{ kg}$,$V = 50 \mathrm{ kg} ÷ \rho_0$再使用一段时间后,瓶内剩余氧气的密度$\rho_3 = \frac{m_{\mathrm{氧3}}}{V} = \frac{15 \mathrm{ kg} - m_{\mathrm{瓶}}}{V} = \frac{15 \mathrm{ kg} - 5 \mathrm{ kg}}{50 \mathrm{ kg} ÷ \rho_0} = \frac{1}{5}\rho_0$,故C正确.
9. (2025·江苏南京期中·3分)两只相同的烧杯均装满水,将一个实心铜块和一个实心铅块分别投入两烧杯中(ρ₍铜₎=8.9×10³kg/m³,ρ₍铅₎=11.3×10³kg/m³,ρ₍水₎=1.0×10³kg/m³),测得两杯总质量相等,下列说法正确的是 (
A.铜块质量大
B.铅块质量大
C.铅块和铜块质量一样大
D.条件不足,无法判断
A
)A.铜块质量大
B.铅块质量大
C.铅块和铜块质量一样大
D.条件不足,无法判断
答案:9. A 解析:两只相同的烧杯均装满水,设其质量均为$m_0$,将铜块投入水中,有水溢出,溢出水后的总质量$m_1 = m_0 + m_{\mathrm{铜}} - m_{\mathrm{溢1}}$,将铅块投入水中,有水溢出,溢出水后的总质量$m_2 = m_0 + m_{\mathrm{铅}} - m_{\mathrm{溢2}}$,由题意可知,$m_1 = m_2$,即$m_0 + m_{\mathrm{铜}} - m_{\mathrm{溢1}} = m_0 + m_{\mathrm{铅}} - m_{\mathrm{溢2}}$,$m_{\mathrm{铜}} - m_{\mathrm{溢1}} = m_{\mathrm{铅}} - m_{\mathrm{溢2}}$,金属块浸没水中,排开(溢出)水的体积等于金属块的体积,由$\rho = \frac{m}{V}$可得,$\rho_{\mathrm{铜}} V_{\mathrm{铜}} - \rho_{\mathrm{水}} V_{\mathrm{铜}} = \rho_{\mathrm{铅}} V_{\mathrm{铅}} - \rho_{\mathrm{水}} V_{\mathrm{铅}}$,$(\rho_{\mathrm{铜}} - \rho_{\mathrm{水}})V_{\mathrm{铜}} = (\rho_{\mathrm{铅}} - \rho_{\mathrm{水}})V_{\mathrm{铅}}$,$\frac{V_{\mathrm{铜}}}{V_{\mathrm{铅}}} = \frac{\rho_{\mathrm{铅}} - \rho_{\mathrm{水}}}{\rho_{\mathrm{铜}} - \rho_{\mathrm{水}}} = \frac{11.3 \mathrm{ g/cm}^3 - 1.0 \mathrm{ g/cm}^3}{8.9 \mathrm{ g/cm}^3 - 1.0 \mathrm{ g/cm}^3} = \frac{103}{79}$,铜块与铅块的质量之比$\frac{m_{\mathrm{铜}}}{m_{\mathrm{铅}}} = \frac{\rho_{\mathrm{铜}} V_{\mathrm{铜}}}{\rho_{\mathrm{铅}} V_{\mathrm{铅}}} = \frac{8.9 \mathrm{ g/cm}^3 × 103}{11.3 \mathrm{ g/cm}^3 × 79} = \frac{9167}{8927} > 1$,所以$m_{\mathrm{铜}} > m_{\mathrm{铅}}$,即铜块的质量大,故A正确.
10. 新趋势 学科融合 (2025·天津二模·2分)化学老师拿出了一瓶浸泡着钠块的煤油,想知晓里面剩余钠的质量,但由于钠易与空气发生化学反应而变质,因此不能将其随意拿出称量。小明找来了一个相同的密封瓶倒入煤油,如图,两瓶液面相平,测得其总质量分别为m₁、m₂,已知煤油和钠的密度分别为ρ₁、ρ₂(ρ₁<ρ₂),则瓶中金属钠的质量m₍钠₎=
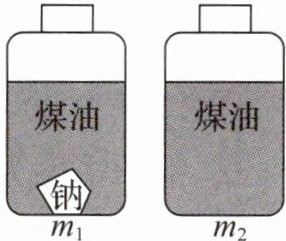
$\frac{\rho_2(m_1 - m_2)}{\rho_2 - \rho_1}$
。若在称量过程中m₂测量值偏大,则计算出的m₍钠₎偏小
(选填“偏大”“偏小”或“无法确认”)。
答案:10. $\frac{\rho_2(m_1 - m_2)}{\rho_2 - \rho_1}$ 偏小 解析:两瓶液面相平,则体积相等,测得其总质量分别为$m_1$、$m_2$,则有$\frac{m_{\mathrm{钠}}}{\rho_2} + \frac{m_{\mathrm{油1}}}{\rho_1} = \frac{m_2}{\rho_1}$,即$\frac{m_{\mathrm{钠}}}{\rho_2} + \frac{m_1 - m_{\mathrm{钠}}}{\rho_1} = \frac{m_2}{\rho_1}$,解得$m_{\mathrm{钠}} = \frac{\rho_2(m_1 - m_2)}{\rho_2 - \rho_1}$;若在称量过程中$m_2$测量值偏大,由$m_{\mathrm{钠}} = \frac{\rho_2(m_1 - m_2)}{\rho_2 - \rho_1}$可知,计算出的$m_{\mathrm{钠}}$偏小.
解析:
$\frac{\rho_2(m_1 - m_2)}{\rho_2 - \rho_1}$;偏小
11. (2025·天津期末·2分)甲、乙两个正方体实心玻璃砖,棱长之比l₍甲₎∶l₍乙₎=3∶2,则ρ₍甲₎∶ρ₍乙₎=

$1:1$
;在玻璃砖内嵌入金属丝制作的各种图案就可以制成精美的工艺品,现有一大一小且中间嵌有大小相同的金属月季花正方体玻璃工艺品A、B,如图,其质量分别为m₍A₎、m₍B₎,棱长分别为l₍A₎、l₍B₎,通过这些数据可推导出玻璃砖的密度为$\frac{m_A - m_B}{l_A^3 - l_B^3}$
。
答案:11. $1:1$ $\frac{m_A - m_B}{l_A^3 - l_B^3}$ 解析:甲、乙两个正方体实心玻璃砖,材质相同,密度相同,则$\rho_{\mathrm{甲}}:\rho_{\mathrm{乙}} = 1:1$;现有一大一小且中间嵌有大小相同的金属月季花正方体玻璃工艺品A、B,二者质量和体积相差的部分都是玻璃,则多出的玻璃的质量$m = m_A - m_B$,体积$V = l_A^3 - l_B^3$,则玻璃砖的密度$\rho = \frac{m}{V} = \frac{m_A - m_B}{l_A^3 - l_B^3}$.
解析:
$1:1$;$\frac{m_A - m_B}{l_A^3 - l_B^3}$