1. $39×19$的积大约是(
800
),积的最高位是(百
)位。$25×40$的积是(四
)位数,积的末尾有(3
)个0。答案:1. 800 百 四 3
解析:
800;百;四;3
2. 把一筐桃平均分给6人,每人分得这些桃的$\frac{( )}{( )}$;如果平均分给8人,那么5人共分得这些桃的$\frac{( )}{( )}$。
答案:2. $\frac{1}{6}$ $\frac{5}{8}$
3. $3$分米$=\frac{( )}{( )}$米,写成小数是(
0.3
)米,写成小数后读作(零点三
)米。答案:3. $\frac{3}{10}$ 0.3 零点三
4. 在$◯$里填“$>$”“$<$”或“$=$”。
$16×51◯15×69$ $\frac{7}{10}$角$◯0.7$元 $100$天$◯$一个季度
$25×16◯25×4×4$ $98×0◯0×1$ $\frac{7}{8}◯\frac{5}{8}$
$16×51◯15×69$ $\frac{7}{10}$角$◯0.7$元 $100$天$◯$一个季度
$25×16◯25×4×4$ $98×0◯0×1$ $\frac{7}{8}◯\frac{5}{8}$
答案:4. < < > = = >
解析:
16×51<15×69
$\frac{7}{10}$角<0.7元
100天>一个季度
25×16=25×4×4
98×0=0×1
$\frac{7}{8}$>$\frac{5}{8}$
$\frac{7}{10}$角<0.7元
100天>一个季度
25×16=25×4×4
98×0=0×1
$\frac{7}{8}$>$\frac{5}{8}$
5. 新情境 生活应用 李爷爷把收获的大米装在同样大的袋子里,一共装了80袋。他从中任意抽出5袋称了一下,质量分别是$18kg$、$21kg$、$19kg$、$22kg$、$20kg$。这些大米大约一共重(
1600
)kg。答案:5. 1600
解析:
18+21+19+22+20=100(kg)
100÷5=20(kg)
20×80=1600(kg)
100÷5=20(kg)
20×80=1600(kg)
6. 光明小学的操场上有一个攀爬架(如图),攀爬架中间有很多横杆,这些横杆的长度都(
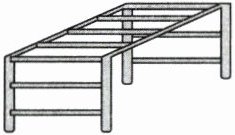
相等
),理由是(平行线之间的距离处处相等
)。
答案:6. 相等 平行线之间的距离处处相等
7. 新情境 自然科普 “人有悲欢离合,月有阴晴圆缺。”月相的变化顺序如图所示,从新月开始,第101个月相是(

满月
)。
答案:7. 满月
解析:
观察月相变化顺序,从新月开始依次为:新月、娥眉月、上弦月、盈凸月、满月、亏凸月、下弦月、残月,共8种月相为一个周期。
计算101除以8的商和余数:$101÷8 = 12······5$,其中商为12,余数为5。
余数为5,对应周期中的第5个月相,即满月。
满月
计算101除以8的商和余数:$101÷8 = 12······5$,其中商为12,余数为5。
余数为5,对应周期中的第5个月相,即满月。
满月
8. 如右图,直线$a$和直线$b$互相垂直。$∠1=∠2$,$∠3=30^{\circ}$,$∠1=( )^{\circ}$,$∠2+∠4=( )^{\circ}$。
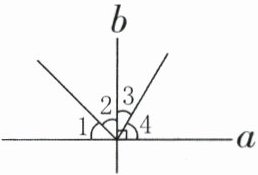

答案:8. 45 105 解析:因为直线a和直线b互相垂直,所以∠1+∠2=90°,∠3+∠4=90°。又因为∠1=∠2,∠3=30°,所以∠1=∠2=90°÷2=45°,∠4=90° - 30°=60°,则∠2+∠4=45°+60°=105°。
解析:
解:因为直线$a$和直线$b$互相垂直,所以$\angle1+\angle2=90^{\circ}$,$\angle3+\angle4=90^{\circ}$。
又因为$\angle1=\angle2$,所以$\angle1=\angle2=90^{\circ}÷2=45^{\circ}$。
因为$\angle3=30^{\circ}$,所以$\angle4=90^{\circ}-30^{\circ}=60^{\circ}$。
则$\angle2+\angle4=45^{\circ}+60^{\circ}=105^{\circ}$。
45;105
又因为$\angle1=\angle2$,所以$\angle1=\angle2=90^{\circ}÷2=45^{\circ}$。
因为$\angle3=30^{\circ}$,所以$\angle4=90^{\circ}-30^{\circ}=60^{\circ}$。
则$\angle2+\angle4=45^{\circ}+60^{\circ}=105^{\circ}$。
45;105