(1) $\frac{2}{5}$里有(
4
)个$\frac{1}{10}$;$2\frac{5}{7}$里有(19
)个$\frac{1}{7}$。答案:1.(1)4 19
(2) $\frac{(\ )}{8}=18÷24=3÷(\ )=\frac{27}{(\ )}=(\ )$(填小数)
答案:1.(2)6 4 36 0.75
解析:
$\frac{6}{8}=18÷24=3÷4=\frac{27}{36}=0.75$
(3) 现有3千克饮料,将其倒进5个相同的杯子里,正好全部倒满,没有剩余。每个杯子中饮料的质量是3千克的$\frac{(\ )}{(\ )}$,是$\frac{(\ )}{(\ )}$千克,是1千克的$\frac{(\ )}{(\ )}$。
答案:1.(3)$\frac{1}{5}$ $\frac{3}{5}$ $\frac{3}{5}$
(4) (探索规律)已知$\frac{1}{1}+\frac{1}{2}-1=\frac{1}{1×2}$,$\frac{1}{3}+\frac{1}{4}-\frac{1}{2}=\frac{1}{3×4}$,$\frac{1}{5}+\frac{1}{6}-\frac{1}{3}=\frac{1}{5×6}$,$\frac{1}{7}+\frac{1}{8}-\frac{1}{4}=\frac{1}{7×8}$……以此类推,$\frac{1}{41}+\frac{1}{42}-$ (
$\frac{1}{21}$
) $=\frac{1}{(\ )}$。答案:1.(4)$\frac{1}{21}$ $\frac{1}{1722}$
解析:
$\frac{1}{21}$;$41 × 42$
(5) 一个分数与$\frac{5}{7}$相等,若分母减去10后等于1,则这个分数是(
$\frac{25}{35}$
)。答案:1.(5)$\frac{25}{35}$
解析:
设这个分数为$\frac{5x}{7x}$($x$为正整数)。
由分母减去10后等于1,可得$7x - 10 = 5x$。
解得$2x = 10$,$x = 5$。
则分子为$5x = 5×5 = 25$,分母为$7x = 7×5 = 35$。
这个分数是$\frac{25}{35}$。
由分母减去10后等于1,可得$7x - 10 = 5x$。
解得$2x = 10$,$x = 5$。
则分子为$5x = 5×5 = 25$,分母为$7x = 7×5 = 35$。
这个分数是$\frac{25}{35}$。
(1) 盐水中有6克盐和200克水,如果再加入4克盐,那么盐占盐水的(
A.$\frac{1}{19}$
B.$\frac{1}{20}$
C.$\frac{1}{21}$
D.$\frac{2}{103}$
C
)。A.$\frac{1}{19}$
B.$\frac{1}{20}$
C.$\frac{1}{21}$
D.$\frac{2}{103}$
答案:2.(1)C
解析:
盐的总质量:$6 + 4 = 10$克
盐水的总质量:$6 + 200 + 4 = 210$克
盐占盐水的比例:$\frac{10}{210} = \frac{1}{21}$
C
盐水的总质量:$6 + 200 + 4 = 210$克
盐占盐水的比例:$\frac{10}{210} = \frac{1}{21}$
C
(2) 甲、乙、丙三人读同一篇童话故事,甲用了15分钟,乙用了0.2小时,丙用了$\frac{1}{6}$小时,(
A.甲
B.乙
C.丙
D.无法确定谁
C
)读得最快。A.甲
B.乙
C.丙
D.无法确定谁
答案:2.(2)C
解析:
甲用的时间:15分钟 = $\frac{15}{60}$小时 = $\frac{1}{4}$小时 = 0.25小时
乙用的时间:0.2小时
丙用的时间:$\frac{1}{6}$小时 ≈ 0.167小时
因为0.167 < 0.2 < 0.25,所以丙读得最快。
C
乙用的时间:0.2小时
丙用的时间:$\frac{1}{6}$小时 ≈ 0.167小时
因为0.167 < 0.2 < 0.25,所以丙读得最快。
C
(3) 学校合唱队的男生人数是女生人数的$\frac{1}{3}$,男生人数占合唱队总人数的(
A.$\frac{1}{4}$
B.$\frac{1}{5}$
C.$\frac{1}{6}$
D.$\frac{3}{4}$
A
)。A.$\frac{1}{4}$
B.$\frac{1}{5}$
C.$\frac{1}{6}$
D.$\frac{3}{4}$
答案:2.(3)A
解析:
设女生人数为$3x$,则男生人数为$x$,总人数为$3x + x = 4x$,男生人数占总人数的比例为$\frac{x}{4x} = \frac{1}{4}$。A
3. 计算下面各题,能简算的要简算。
$1-\frac{3}{8}+\frac{5}{8}$
$\frac{8}{15}-(\frac{7}{12}-\frac{7}{15})-\frac{5}{12}$
$1-\frac{3}{8}+\frac{5}{8}$
$\frac{8}{15}-(\frac{7}{12}-\frac{7}{15})-\frac{5}{12}$
答案:3.$\frac{5}{4}$ 0
解析:
$1-\frac{3}{8}+\frac{5}{8}$
$=\frac{8}{8}-\frac{3}{8}+\frac{5}{8}$
$=\frac{5}{8}+\frac{5}{8}$
$=\frac{10}{8}$
$=\frac{5}{4}$
$\frac{8}{15}-(\frac{7}{12}-\frac{7}{15})-\frac{5}{12}$
$=\frac{8}{15}-\frac{7}{12}+\frac{7}{15}-\frac{5}{12}$
$=(\frac{8}{15}+\frac{7}{15})-(\frac{7}{12}+\frac{5}{12})$
$=1-1$
$=0$
$=\frac{8}{8}-\frac{3}{8}+\frac{5}{8}$
$=\frac{5}{8}+\frac{5}{8}$
$=\frac{10}{8}$
$=\frac{5}{4}$
$\frac{8}{15}-(\frac{7}{12}-\frac{7}{15})-\frac{5}{12}$
$=\frac{8}{15}-\frac{7}{12}+\frac{7}{15}-\frac{5}{12}$
$=(\frac{8}{15}+\frac{7}{15})-(\frac{7}{12}+\frac{5}{12})$
$=1-1$
$=0$
4. (易错题)修一条长$\frac{9}{5}$千米的路,甲队先修了全长的$\frac{3}{8}$,乙队接着修了全长的$\frac{1}{4}$。剩下的两队合修,两队再修全长的几分之几就修了这条路的$\frac{8}{9}$?
答案:4.$\frac{8}{9}-\frac{1}{4}-\frac{3}{8}=\frac{19}{72}$ 易错分析:$\frac{9}{5}$千米是干扰条件,
全长是单位“1”,问题要求的是比全长的$\frac{8}{9}$还差多少。
全长是单位“1”,问题要求的是比全长的$\frac{8}{9}$还差多少。
5. (生活应用)明明是个爱用数学记录生活的小朋友,你能根据他提供的信息解决问题吗?
一天有24小时,我调查20人,发现大家一般用全天的$\frac{3}{8}$睡眠,用全天的$\frac{1}{8}$进餐,用全天的$\frac{1}{6}$做各种活动,剩下的时间用于学习和工作。
学习和工作的时间占全天的几分之几?
一天有24小时,我调查20人,发现大家一般用全天的$\frac{3}{8}$睡眠,用全天的$\frac{1}{8}$进餐,用全天的$\frac{1}{6}$做各种活动,剩下的时间用于学习和工作。
学习和工作的时间占全天的几分之几?
答案:5.1 - $\frac{3}{8}$ - $\frac{1}{8}$ - $\frac{1}{6}$ = $\frac{1}{3}$
6. 在$◯$里填合适的分数,使每个正方形四个角上的分数加起来都等于1。
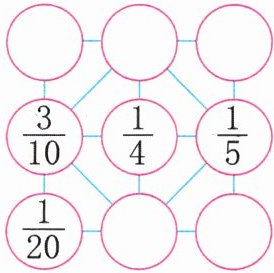

答案:6.$\frac{7}{20}$ $\frac{1}{10}$ $\frac{9}{20}$ $\frac{2}{5}$ $\frac{3}{20}$
解析:先找突破口,本题突破口在左下的正方形,要满足四个角上的分数的和是1,则可知剩下的分数为1 - $\frac{3}{10}$ - $\frac{1}{20}$ - $\frac{1}{4}$ = $\frac{2}{5}$,那么右下角可依此突破,列式为1 - $\frac{2}{5}$ - $\frac{1}{5}$ - $\frac{1}{4}$ = $\frac{3}{20}$,第一行中间的分数为1 - $\frac{3}{10}$ - $\frac{2}{5}$ = $\frac{1}{10}$,剩下依此计算即可。
解析:先找突破口,本题突破口在左下的正方形,要满足四个角上的分数的和是1,则可知剩下的分数为1 - $\frac{3}{10}$ - $\frac{1}{20}$ - $\frac{1}{4}$ = $\frac{2}{5}$,那么右下角可依此突破,列式为1 - $\frac{2}{5}$ - $\frac{1}{5}$ - $\frac{1}{4}$ = $\frac{3}{20}$,第一行中间的分数为1 - $\frac{3}{10}$ - $\frac{2}{5}$ = $\frac{1}{10}$,剩下依此计算即可。