3. 解方程。(9分)
$x - \frac{5}{12} = \frac{1}{10}$ $2.7x + 7.3x = 2.3$ $6 × 0.3 + 2x = 10.8$
$x - \frac{5}{12} = \frac{1}{10}$ $2.7x + 7.3x = 2.3$ $6 × 0.3 + 2x = 10.8$
答案：3.x=$\frac{31}{60}$ x=0.23 x=4.5
解析：
解：$x - \frac{5}{12} = \frac{1}{10}$
$x = \frac{1}{10} + \frac{5}{12}$
$x = \frac{6}{60} + \frac{25}{60}$
$x = \frac{31}{60}$
解：$2.7x + 7.3x = 2.3$
$10x = 2.3$
$x = 0.23$
解：$6 × 0.3 + 2x = 10.8$
$1.8 + 2x = 10.8$
$2x = 10.8 - 1.8$
$2x = 9$
$x = 4.5$
$x = \frac{1}{10} + \frac{5}{12}$
$x = \frac{6}{60} + \frac{25}{60}$
$x = \frac{31}{60}$
解：$2.7x + 7.3x = 2.3$
$10x = 2.3$
$x = 0.23$
解：$6 × 0.3 + 2x = 10.8$
$1.8 + 2x = 10.8$
$2x = 10.8 - 1.8$
$2x = 9$
$x = 4.5$
1. 一台碾米机每小时碾米$\frac{5}{8}$ 吨,$\frac{3}{4}$ 小时碾米多少吨? 先在左下图中表示出来,再列式计算。
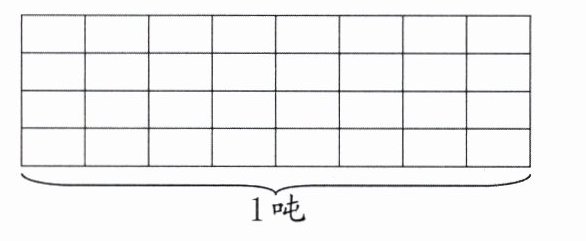
列式计算:
列式计算:
$\frac{5}{8}$×$\frac{3}{4}$=$\frac{15}{32}$(吨)
答案：
1.
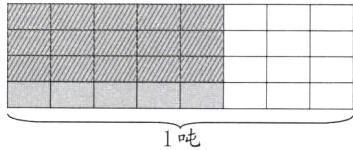
$\frac{5}{8}$×$\frac{3}{4}$=$\frac{15}{32}$(吨)
1.
$\frac{5}{8}$×$\frac{3}{4}$=$\frac{15}{32}$(吨)
2. 用长10厘米、宽6厘米的长方形硬纸板(如右上图)做成一个棱长为2厘米的正方体纸盒。
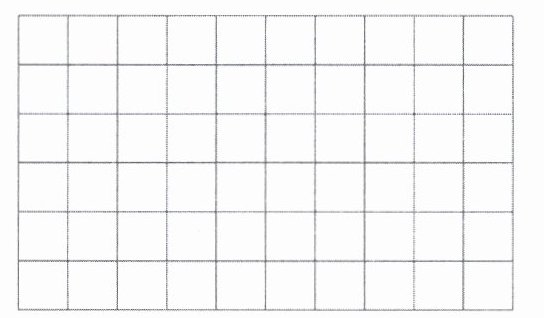
(1) 应如何剪(接头处忽略不计)? 在图中涂色表示要剪出的图形(即正方体纸盒的展开图)。
(2) 做成的纸盒的体积是(
(1) 应如何剪(接头处忽略不计)? 在图中涂色表示要剪出的图形(即正方体纸盒的展开图)。
(2) 做成的纸盒的体积是(
8
)立方厘米。答案：
2.(1)画法不唯一，如图所示 (2)8
2.(1)画法不唯一，如图所示 (2)8
3. 新趋势算法探究 用如图①所示的方法可以解决求三角形面积的问题,类比这样的方法,你能求出图②中几何体的体积吗? 画出草图并列式计算。
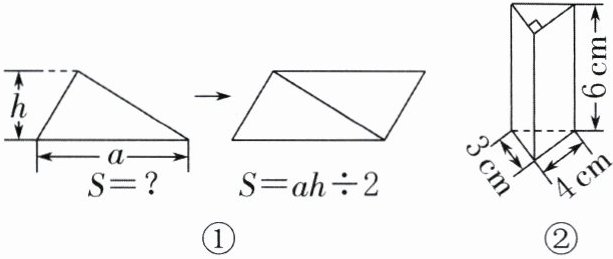
答案：
3.
3×4×6÷2=36(cm³)
3.
3×4×6÷2=36(cm³)1. 一张正方形纸的边长是$\frac{8}{9}$ 分米,把它沿一个方向对折再对折后,得到一个长方形。这个长方形的面积是多少平方分米? (5分)
答案：1.$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{4}$ $\frac{8}{9}$×$\frac{8}{9}$×$\frac{1}{4}$=$\frac{16}{81}$(平方分米)
解析：
$\frac{1}{2} × \frac{1}{2} = \frac{1}{4}$
$\frac{8}{9} × \frac{8}{9} × \frac{1}{4} = \frac{64}{81} × \frac{1}{4} = \frac{16}{81}$(平方分米)
$\frac{8}{9} × \frac{8}{9} × \frac{1}{4} = \frac{64}{81} × \frac{1}{4} = \frac{16}{81}$(平方分米)