1. 用简便方法计算。
25×32×125
2×8×6×35×125×5
125×72×9
5×25×125×64
25×32×125
2×8×6×35×125×5
125×72×9
5×25×125×64
答案:1. $25×32×125$
$=25×4×8×125$
$=(25×4)×(8×125)$
$=100×1000$
$=100000$
$2×8×6×35×125×5$
$=(2×5)×(8×125)×(6×35)$
$=10×1000×210$
$=2100000$
$125×72×9$
$=125×(8×9)×9$
$=(125×8)×(9×9)$
$=1000×81$
$=81000$
$5×25×125×64$
$=5×25×125×(2×4×8)$
$=(5×2)×(25×4)×(125×8)$
$=10×100×1000$
$=1000000$
$=25×4×8×125$
$=(25×4)×(8×125)$
$=100×1000$
$=100000$
$2×8×6×35×125×5$
$=(2×5)×(8×125)×(6×35)$
$=10×1000×210$
$=2100000$
$125×72×9$
$=125×(8×9)×9$
$=(125×8)×(9×9)$
$=1000×81$
$=81000$
$5×25×125×64$
$=5×25×125×(2×4×8)$
$=(5×2)×(25×4)×(125×8)$
$=10×100×1000$
$=1000000$
2. 楠楠在计算 3×(○+△)时,将算式看成了 3×○+△,结果比原来小了 12。如果将 12 表示的含义在图上圈出来,下面正确的是(
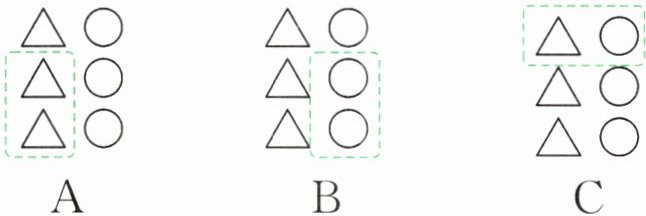
A
)。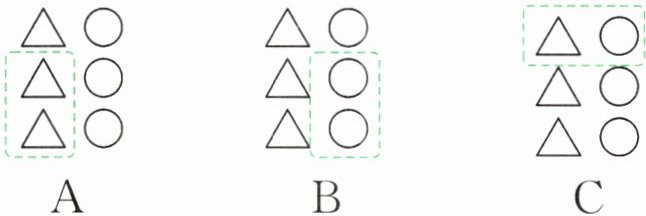
答案:
2. A 【提示】$3×(○+△)=3×○+3×△$比$3×○+△$多了 2 个△。
2. A 【提示】$3×(○+△)=3×○+3×△$比$3×○+△$多了 2 个△。

3. 丽丽在做题时不小心把 6×(□+2)错写成了 6×□+2,她算出的结果与正确的结果相差多少?
答案:
3. $6×2 - 2 = 10$
【提示】$6×(□+2)=6×□+6×2=6×□+12$,$6×□+12$比$6×□+2$多 10。



3. $6×2 - 2 = 10$
【提示】$6×(□+2)=6×□+6×2=6×□+12$,$6×□+12$比$6×□+2$多 10。




4. 欢欢在计算(200-25)×□时,漏看了小括号,算出的结果是 100,求这道题的正确结果。
答案:4. $(200 - 100)÷25 = 4$
$(200 - 25)×4 = 700$
【提示】$200 - 25×□ = 100$,$□ = 4$,$(200 - 25)×□=(200 - 25)×4 = 700$。
方法归纳 错中求解问题
这类错中求解问题,可以先“将错就错”,求出其中的未知数,再将未知数代入到原来的算式中求出正确的答案。
$(200 - 25)×4 = 700$
【提示】$200 - 25×□ = 100$,$□ = 4$,$(200 - 25)×□=(200 - 25)×4 = 700$。
方法归纳 错中求解问题
这类错中求解问题,可以先“将错就错”,求出其中的未知数,再将未知数代入到原来的算式中求出正确的答案。
5. 小明在计算 ○+5×8 时错看成了(○+5)×8,先算加法,再算乘法。这样算出来的结果比正确结果多了 42,正确的结果是多少?
答案:
5. $42÷(8 - 1) = 6$
$6 + 5×8 = 46$
【提示】小明计算时错看成了$(○+5)×8$,利用乘法分配律,算式可以转化为$○×8 + 5×8$,与原来的算式相比,多了$8 - 1 = 7$(个)○,结果多了 42,即可求出○为$42÷7 = 6$,据此求出正确的结果。


5. $42÷(8 - 1) = 6$
$6 + 5×8 = 46$
【提示】小明计算时错看成了$(○+5)×8$,利用乘法分配律,算式可以转化为$○×8 + 5×8$,与原来的算式相比,多了$8 - 1 = 7$(个)○,结果多了 42,即可求出○为$42÷7 = 6$,据此求出正确的结果。


