1. 从长度为 2 厘米、3 厘米、4 厘米、5 厘米和 7 厘米的 5 根小棒中选择 3 根围成一个三角形,一共有多少种情况?
答案:1. 一共有 5 种情况:7 厘米、3 厘米和 5 厘米;7 厘米、4 厘米和 5 厘米;5 厘米、2 厘米和 4 厘米;5 厘米、3 厘米和 4 厘米;4 厘米、2 厘米和 3 厘米。
【提示】先将选择三根小棒的情况列举出来,再根据三角形的三边关系,判断每种情况能否围成三角形。
【提示】先将选择三根小棒的情况列举出来,再根据三角形的三边关系,判断每种情况能否围成三角形。
2. 明明用长度为 4 厘米、6 厘米、8 厘米、10 厘米和 12 厘米的 5 根小棒中的 3 根围成一个三角形,一共有多少种情况?
答案:2. 一共有 7 种情况:12 厘米、10 厘米和 8 厘米;12 厘米、10 厘米和 6 厘米;12 厘米、10 厘米和 4 厘米;12 厘米、8 厘米和 6 厘米;10 厘米、8 厘米和 6 厘米;10 厘米、8 厘米和 4 厘米;8 厘米、6 厘米和 4 厘米。
【提示】先将选择三根小棒的情况列举出来,再根据三角形的三边关系,判断每种情况能否围成三角形。
【提示】先将选择三根小棒的情况列举出来,再根据三角形的三边关系,判断每种情况能否围成三角形。
3. 如下图,已知 $∠1 = ∠5 = 90^{\circ}$,$∠4 = 75^{\circ}$,$∠3$ 的度数是(
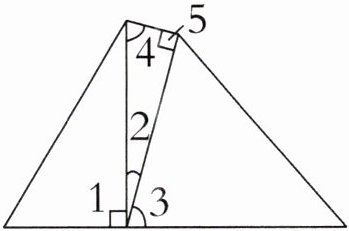
A.$75^{\circ}$
B.$70^{\circ}$
C.$90^{\circ}$
D.$15^{\circ}$
A
)。
A.$75^{\circ}$
B.$70^{\circ}$
C.$90^{\circ}$
D.$15^{\circ}$
答案:3. A
【提示】在中间的三角形中,$∠ 2 = 180^{\circ} - 90^{\circ} - 75^{\circ} = 15^{\circ}$,又因为$∠ 1 + ∠ 2 + ∠ 3 = 180^{\circ}$,所以$∠ 3 = 180^{\circ} - 90^{\circ} - 15^{\circ} = 75^{\circ}$。
【提示】在中间的三角形中,$∠ 2 = 180^{\circ} - 90^{\circ} - 75^{\circ} = 15^{\circ}$,又因为$∠ 1 + ∠ 2 + ∠ 3 = 180^{\circ}$,所以$∠ 3 = 180^{\circ} - 90^{\circ} - 15^{\circ} = 75^{\circ}$。
4. 如右下图所示,三角形 $ABC$ 中,已知 $∠ACB = 120^{\circ}$,$∠1 = ∠2$,$∠BAC = 25^{\circ}$,求 $∠3$ 的度数。
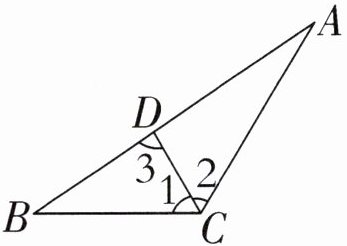

答案:4. $∠ 1 = ∠ 2 = 120^{\circ} ÷ 2 = 60^{\circ}$
$∠ CDA = 180^{\circ} - 60^{\circ} - 25^{\circ} = 95^{\circ}$
$∠ 3 = 180^{\circ} - 95^{\circ} = 85^{\circ}$
【提示】先求出$∠ 1$、$∠ 2$的度数,根据三角形的内角和是$180^{\circ}$,求出$∠ CDA$的度数,再用$180^{\circ} - ∠ CDA$即可。
$∠ CDA = 180^{\circ} - 60^{\circ} - 25^{\circ} = 95^{\circ}$
$∠ 3 = 180^{\circ} - 95^{\circ} = 85^{\circ}$
【提示】先求出$∠ 1$、$∠ 2$的度数,根据三角形的内角和是$180^{\circ}$,求出$∠ CDA$的度数,再用$180^{\circ} - ∠ CDA$即可。
5. 将长方形 $ABCD$ 沿 $BF$ 边翻折,点 $C$ 刚好落在 $AD$ 边上的点 $E$ 处。已知 $∠EFB = 70^{\circ}$,求 $∠ABE$ 的度数。
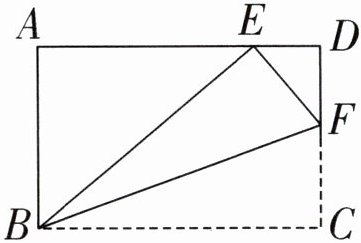

答案:5. $∠ EBF = 180^{\circ} - 90^{\circ} - 70^{\circ} = 20^{\circ}$
$∠ ABE = 90^{\circ} - 20^{\circ} × 2 = 50^{\circ}$
【提示】本题可根据长方形的性质和折叠的特点来求解$∠ ABE$的度数。
$∠ ABE = 90^{\circ} - 20^{\circ} × 2 = 50^{\circ}$
【提示】本题可根据长方形的性质和折叠的特点来求解$∠ ABE$的度数。
6. 求右下图中 $∠A + ∠B + ∠C + ∠D + ∠E$ 的度数。
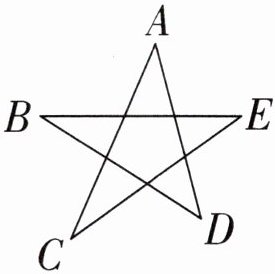

答案:6. $5 × 180^{\circ} - (5 - 2) × 180^{\circ} = 360^{\circ}$
$360^{\circ} ÷ 2 = 180^{\circ}$
【提示】本题可利用多边形内角和$= (n - 2) × 180^{\circ}$和三角形内角和等于$180^{\circ}$来求解。
$360^{\circ} ÷ 2 = 180^{\circ}$
【提示】本题可利用多边形内角和$= (n - 2) × 180^{\circ}$和三角形内角和等于$180^{\circ}$来求解。