4. 基于先进的技术,无人快递车可以通过智能调度增加派件量。据试点区域数据统计,一辆传统电动三轮车一天的派件量仅为一辆无人快递车一天派件量的$$\frac{1}{3}$$。如果一辆无人快递车和一辆传统电动三轮车一天的派件量总和是2800件,那么一辆无人快递车和一辆传统电动三轮车一天的派件量各是多少件?
答案:4. 设一辆无人快递车一天的派件量为 x 件,则传统电动三轮车一天的派件量为 $\frac{1}{3}$x 件。
x + $\frac{1}{3}$x = 2800 x = 2100
$\frac{1}{3}$×2100 = 700(件)
[提示]将一辆无人快递车一天的派件量设为 x 件,则一辆传统三轮车一天的派件量用 $\frac{1}{3}$x 件表示,根据两车一天的派件量的总和为 2800 件列出方程,解答即可。
x + $\frac{1}{3}$x = 2800 x = 2100
$\frac{1}{3}$×2100 = 700(件)
[提示]将一辆无人快递车一天的派件量设为 x 件,则一辆传统三轮车一天的派件量用 $\frac{1}{3}$x 件表示,根据两车一天的派件量的总和为 2800 件列出方程,解答即可。
5. 甲、乙两地相距350千米,一辆客车和一辆货车同时从甲、乙两地相向而行。客车的速度是75千米/时,货车的速度是65千米/时,两车相遇时客车超过甲、乙两地中点多少千米?
答案:5. 350÷(75 + 65) = 2.5(小时)
75×2.5 = 187.5(千米)
187.5 - 350÷2 = 12.5(千米)
[提示]根据“相遇时间 = 路程÷速度和”,求出相遇时间,然后用客车的速度×相遇时间得到相遇时客车行驶的路程,甲地到甲、乙两地中点是 350÷2 = 175(千米),再用客车行驶的路程减去甲地到甲、乙两地中点的路程就得到相遇时客车超过甲、乙两地中点的距离。
75×2.5 = 187.5(千米)
187.5 - 350÷2 = 12.5(千米)
[提示]根据“相遇时间 = 路程÷速度和”,求出相遇时间,然后用客车的速度×相遇时间得到相遇时客车行驶的路程,甲地到甲、乙两地中点是 350÷2 = 175(千米),再用客车行驶的路程减去甲地到甲、乙两地中点的路程就得到相遇时客车超过甲、乙两地中点的距离。
6. 陀螺游戏是第五批国家级非物质文化遗产代表性项目。陀螺一般是用木料打磨而成(如下图),打磨这个陀螺至少要用多少立方厘米的木料?如果把这个陀螺装在一个带盖的长方体纸盒中,那么制作这个纸盒至少需要多少平方厘米的纸?(粘贴及折叠处忽略不计)
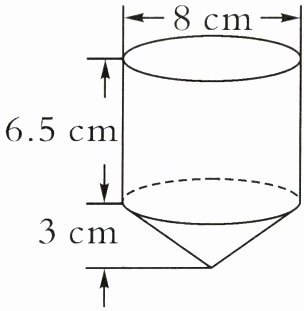

答案:6. (8÷2)²×3.14×6.5 + 3.14×(8÷2)²×3×$\frac{1}{3}$ = 376.8(立方厘米)
6.5 + 3 = 9.5(厘米)
9.5×8×4 + 8×8×2 = 432(平方厘米)
[提示]根据“圆柱体积公式 V = πr²h、圆锥体积公式 V = $\frac{1}{3}$πr²h”,代入数据求出圆柱和圆锥的体积和,就得到打磨这个陀螺至少需要多少立方厘米的木料。制作一个纸盒,这个纸盒的长是 (6.5 + 3)厘米,宽是 8 厘米,高是 8 厘米,根据长方体表面积公式,代入数据,求出纸盒的表面积即可。
6.5 + 3 = 9.5(厘米)
9.5×8×4 + 8×8×2 = 432(平方厘米)
[提示]根据“圆柱体积公式 V = πr²h、圆锥体积公式 V = $\frac{1}{3}$πr²h”,代入数据求出圆柱和圆锥的体积和,就得到打磨这个陀螺至少需要多少立方厘米的木料。制作一个纸盒,这个纸盒的长是 (6.5 + 3)厘米,宽是 8 厘米,高是 8 厘米,根据长方体表面积公式,代入数据,求出纸盒的表面积即可。