1. 下面的计算对吗?对的在(
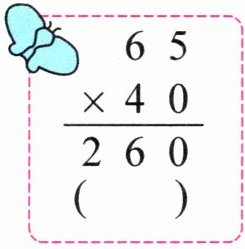
$\begin{array}{r} 65\\ ×40\\ \hline 260\end{array}$
(
改正:
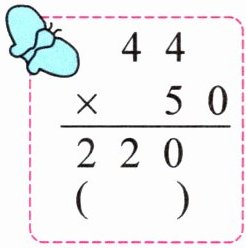
$\begin{array}{r} 44\\ ×50\\ \hline 220\end{array}$
(
改正:
×
)里画“√”,错的在()里画“×”,并改正。
$\begin{array}{r} 65\\ ×40\\ \hline 260\end{array}$
(
×
)改正:
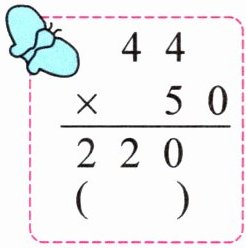
$\begin{array}{r} 44\\ ×50\\ \hline 220\end{array}$
(
×
)改正:
答案:
1. ×
$\begin{array}{r}65 \\× 40 \\\hline2600\end{array}$
×
$\begin{array}{r}44 \\× 50 \\\hline2200\end{array}$

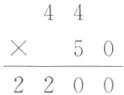
1. ×
$\begin{array}{r}65 \\× 40 \\\hline2600\end{array}$
×
$\begin{array}{r}44 \\× 50 \\\hline2200\end{array}$


2. 算一算,填一填。

(1)上面哪几组中的两道乘法算式的积相等?(
(2)我发现:一个数连续乘两个数,就等于这个数乘这两个数的(
(3)根据前面的发现,在括号里填合适的数,使等式成立。
$55×2×45=55×($
$48×4×($

(1)上面哪几组中的两道乘法算式的积相等?(
②③
)(填序号)(2)我发现:一个数连续乘两个数,就等于这个数乘这两个数的(
积
)。(3)根据前面的发现,在括号里填合适的数,使等式成立。
$55×2×45=55×($
90
$)$$48×4×($
15
$)=48×60$答案:2. ① 1200 680 ② 480 480 ③ 1000 1000
(1) ②③ (2) 积 (3) 90 15
(1) ②③ (2) 积 (3) 90 15
3. 两个两位数相乘,若这两个数的末尾共有 1 个 0,则积的末尾(
A.一定只有 1 个 0
B.不可能有 2 个 0
C.可能有 3 个 0
C
)。A.一定只有 1 个 0
B.不可能有 2 个 0
C.可能有 3 个 0
答案:3. C
4. 新情境 真实生活 超市上午购进 20 箱番茄。

原来每箱的价格是 98 元,现在开展促销活动,每箱的价格是 86 元。
(1)促销期间这些番茄能卖(
(2)请根据算式$98-86=12$(元)和$12×20=240$(元),提出一个数学问题:(

原来每箱的价格是 98 元,现在开展促销活动,每箱的价格是 86 元。
(1)促销期间这些番茄能卖(
1720
)元。(2)请根据算式$98-86=12$(元)和$12×20=240$(元),提出一个数学问题:(
这些番茄在促销期间少卖了多少元
)。答案:4. (1) 1720 (2) 这些番茄在促销期间少卖了多少元
5. 两个数的乘积是第一个乘数的 15 倍,是第二个乘数的 40 倍,这两个数的乘积是(
600
)。答案:5. 600 解析 两个数的乘积是第一个乘数的15倍,说明第二个乘数是15,是第二个乘数的40倍,说明第一个乘数是40,这两个数的乘积是$40×15=600$。
解析:
设第一个乘数为$a$,第二个乘数为$b$。
因为两个数的乘积是第一个乘数的15倍,所以$a×b = 15a$,可得$b = 15$;
又因为两个数的乘积是第二个乘数的40倍,所以$a×b = 40b$,可得$a = 40$;
则这两个数的乘积是$a×b = 40×15 = 600$。
600
因为两个数的乘积是第一个乘数的15倍,所以$a×b = 15a$,可得$b = 15$;
又因为两个数的乘积是第二个乘数的40倍,所以$a×b = 40b$,可得$a = 40$;
则这两个数的乘积是$a×b = 40×15 = 600$。
600
6. 仓库里有 12 个红球和 15 个黄球,白球的个数比红球和黄球的总个数的 30 倍多、40 倍少。白球最少有多少个?最多呢?
答案:6. $12+15=27$(个) 最少:$27×30=810$(个) $810+1=811$(个) 最多:$27×40=1080$(个) $1080-1=1079$(个) 解析 白球的个数最少比红球和黄球的总个数的30倍多1,最多比红球和黄球的总个数的40倍少1。
解析:
$12+15=27$(个)
最少:$27×30 + 1=811$(个)
最多:$27×40 - 1=1079$(个)
最少:$27×30 + 1=811$(个)
最多:$27×40 - 1=1079$(个)