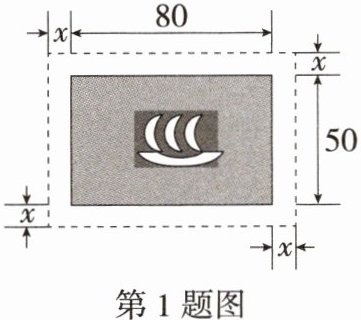
1.「2025山西晋中左权月考」在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是$5400cm^2,$设金色纸边的宽为xcm,那么x满足的方程是(
A. (80+x)(50+x)= 5400
B. (80-2x)(50-2x)= 5400
C. (80+2x)(50+2x)= 5400
D. (80-x)(50-x)= 5400
C
)
A. (80+x)(50+x)= 5400
B. (80-2x)(50-2x)= 5400
C. (80+2x)(50+2x)= 5400
D. (80-x)(50-x)= 5400
答案:C 整个挂图是矩形,长为$(80 + 2x)\text{cm}$,宽为$(50 + 2x)\text{cm}$,∵整个挂图面积是$5400\text{cm}^2$,∴可列方程为$(80 + 2x)(50 + 2x) = 5400$。故选C。
2.「2025湖北宜昌伍家岗期中」如图,某小区规划在一个长为24m、宽为10m的矩形场地ABCD上修建三条同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草。若草坪部分的总面积为$126m^2,$则小路的宽度为______

3
m。
答案:答案 3
解析 设小路的宽度为$x\text{m}$,由平移知识易知草坪部分可看成一个长为$(24 - 2x)\text{m}$,宽为$(10 - x)\text{m}$的矩形,依题意得$(24 - 2x)(10 - x) = 126$,解得$x_1 = 3$,$x_2 = 19$,当$x = 19$时,$10 - x = -9 < 0$,不合题意,舍去,∴$x = 3$。
解析 设小路的宽度为$x\text{m}$,由平移知识易知草坪部分可看成一个长为$(24 - 2x)\text{m}$,宽为$(10 - x)\text{m}$的矩形,依题意得$(24 - 2x)(10 - x) = 126$,解得$x_1 = 3$,$x_2 = 19$,当$x = 19$时,$10 - x = -9 < 0$,不合题意,舍去,∴$x = 3$。
3.跨物理运动「2025广东深圳龙华月考」以初速度v₀竖直上抛的物体的高度h和时间t满足关系式h= v₀t - $\frac{1}{2}gt^{2}$(g为重力加速度,g≈10m/s^2),一个小石子在地面以初速度v₀= 25m/s被向上抛出,则小石子离地20米的时间是(
A. 1s
B. 1s或4s
C. 4s
D. 不能确定
B
)A. 1s
B. 1s或4s
C. 4s
D. 不能确定
答案:B 已知以初速度$v_0$竖直上抛的物体的高度$h$和时间$t$满足关系式$h = v_0t - \frac{1}{2}gt^2$($g$为重力加速度,$g \approx 10\text{m/s}^2$),将$h = 20\text{m}$,$v_0 = 25\text{m/s}$,$g \approx 10\text{m/s}^2$代入得$20 = 25t - \frac{1}{2}×10t^2$,解得$t_1 = 1$,$t_2 = 4$,∴经过$1\text{s}$或$4\text{s}$时,小石子离地$20\text{m}$。故选B。
4.「2025广东清远英德期中」如图,在△ABC中,∠ABC= 90°,AB= 8cm,BC= 7cm,动点P,Q分别从点A,B同时开始移动(移动方向如图所示),点P的速度为1cm/s,点Q的速度为2cm/s,点Q移动到C点后停止,点P也随之停止运动,当四边形APQC的面积为$13cm^2$时,点P运动的时间是(

A. 3s
B. 5s
C. 3s或5s
D. 6s
3s
)
A. 3s
B. 5s
C. 3s或5s
D. 6s
答案:A $8 ÷ 1 = 8(\text{s})$,$7 ÷ 2 = \frac{7}{2}(\text{s})$。设运动时间为$t\text{s}(0 < t \leq \frac{7}{2})$,则$AP = t\text{cm}$,$BQ = 2t\text{cm}$,∴$BP = AB - AP = (8 - t)\text{cm}$,根据题意,得$\frac{1}{2}×8×7 - \frac{1}{2}(8 - t)×2t = 13$,整理,得$t^2 - 8t + 15 = 0$,解得$t_1 = 3$,$t_2 = 5$(不符合题意,舍去),∴点$P$运动的时间是$3\text{s}$。故选A。
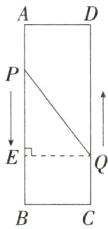
5.「2025广东深圳福田期中,★☆」如图,在矩形ABCD中,AB= 8cm,AD= 3cm,动点P,Q同时出发,点P从A点出发以2cm/s的速度向点B移动,一直到达点B为止,点Q从点C出发以1cm/s的速度向点D移动。请问当点P和点Q的距离是5cm时,P,Q两点出发了( )

A. 4s
B. $\frac{4}{3}$s或4s
C. $\frac{8}{3}$s或8s
D. $\frac{8}{3}$s

A. 4s
B. $\frac{4}{3}$s或4s
C. $\frac{8}{3}$s或8s
D. $\frac{8}{3}$s
答案:
B $8 ÷ 2 = 4(\text{s})$,过点$Q$作$QE \perp AB$于点$E$,则四边形$BCQE$是矩形,如图所示。设运动时间为$t\text{s}(0 < t \leq 4)$,则$AP = 2t\text{cm}$,$CQ = BE = t\text{cm}$,∴$PE = |AB - AP - BE| = |8 - 2t - t| = |8 - 3t|\text{cm}$。根据题意,得$PE^2 + EQ^2 = PQ^2$,即$(8 - 3t)^2 + 3^2 = 5^2$,整理,得$3t^2 - 16t + 16 = 0$,解得$t_1 = \frac{4}{3}$,$t_2 = 4$,∴当点$P$和点$Q$的距离是$5\text{cm}$时,$P$,$Q$两点出发了$\frac{4}{3}\text{s}$或$4\text{s}$。故选B。
B $8 ÷ 2 = 4(\text{s})$,过点$Q$作$QE \perp AB$于点$E$,则四边形$BCQE$是矩形,如图所示。设运动时间为$t\text{s}(0 < t \leq 4)$,则$AP = 2t\text{cm}$,$CQ = BE = t\text{cm}$,∴$PE = |AB - AP - BE| = |8 - 2t - t| = |8 - 3t|\text{cm}$。根据题意,得$PE^2 + EQ^2 = PQ^2$,即$(8 - 3t)^2 + 3^2 = 5^2$,整理,得$3t^2 - 16t + 16 = 0$,解得$t_1 = \frac{4}{3}$,$t_2 = 4$,∴当点$P$和点$Q$的距离是$5\text{cm}$时,$P$,$Q$两点出发了$\frac{4}{3}\text{s}$或$4\text{s}$。故选B。

6.「2025河南平顶山月考,★☆」某社区为了解决停车难的问题,利用一块矩形空地ABCD建了一个小型停车场,其布局如图所示。已知AD= 58m,AB= 22m,阴影部分设计为停车位,其余部分均为宽度为x米的道路。已知停车位的面积(即阴影部分的面积)为$700m^2。$
(1)求道路的宽。
答:道路的宽是
(2)该停车场共有车位70个,据调查分析,当每个车位的月租金为300元时,可全部租出,每个车位的月租金每上涨5元,就会少租出1个车位。当每个车位的月租金上涨多少元时,停车场的月租金收入为21120元,同时尽可能让利于居民?
答:每个车位的月租金上涨
(1)求道路的宽。
答:道路的宽是
4
米。(2)该停车场共有车位70个,据调查分析,当每个车位的月租金为300元时,可全部租出,每个车位的月租金每上涨5元,就会少租出1个车位。当每个车位的月租金上涨多少元时,停车场的月租金收入为21120元,同时尽可能让利于居民?
答:每个车位的月租金上涨
20
元时,停车场的月租金收入为21120元。答案:解析 (1) 道路的宽为$x$米,
由停车位的面积(即阴影部分的面积)为$700\text{m}^2$得,$(58 - 2x)(22 - 2x) = 700$,整理,得$x^2 - 40x + 144 = 0$,
解得$x_1 = 36$(不合题意,舍去),$x_2 = 4$。
答:道路的宽是$4$米。
(2) 设每个车位的月租金上涨$y$元,
根据题意,得$(300 + y)(70 - \frac{y}{5}) = 21120$,
整理,得$y^2 - 50y + 600 = 0$,解得$y_1 = 20$,$y_2 = 30$,
∵尽可能让利于居民,∴$y = 20$。
答:每个车位的月租金上涨$20$元时,停车场的月租金收入为$21120$元。
由停车位的面积(即阴影部分的面积)为$700\text{m}^2$得,$(58 - 2x)(22 - 2x) = 700$,整理,得$x^2 - 40x + 144 = 0$,
解得$x_1 = 36$(不合题意,舍去),$x_2 = 4$。
答:道路的宽是$4$米。
(2) 设每个车位的月租金上涨$y$元,
根据题意,得$(300 + y)(70 - \frac{y}{5}) = 21120$,
整理,得$y^2 - 50y + 600 = 0$,解得$y_1 = 20$,$y_2 = 30$,
∵尽可能让利于居民,∴$y = 20$。
答:每个车位的月租金上涨$20$元时,停车场的月租金收入为$21120$元。