7.新课标空间观念「2025山东青岛即墨月考」综合实践——用矩形硬纸片制作无盖纸盒。
如图1,有一张长30cm,宽16cm的长方形硬纸片,裁去角上同样大小的四个小正方形之后,折成如图2所示的无盖纸盒。(硬纸片厚度忽略不计)
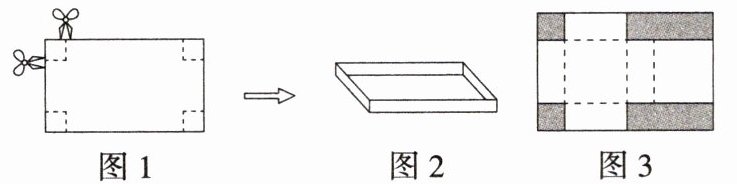
(1)若剪去的小正方形的边长为2cm,则纸盒底面长方形的长为
(2)若纸盒的底面积为$240cm^2,$请计算剪去的小正方形的边长。
(3)如图3,小明先在原矩形硬纸片的两个角各剪去一个同样大小的正方形(阴影部分),经过思考他发现,再剪去两个同样大小的矩形后,可将剩余部分折成一个有盖纸盒。若折成的有盖长方体纸盒的表面积为$412cm^2,$请计算剪去的正方形的边长。
如图1,有一张长30cm,宽16cm的长方形硬纸片,裁去角上同样大小的四个小正方形之后,折成如图2所示的无盖纸盒。(硬纸片厚度忽略不计)

(1)若剪去的小正方形的边长为2cm,则纸盒底面长方形的长为
26
cm,宽为12
cm。(2)若纸盒的底面积为$240cm^2,$请计算剪去的小正方形的边长。
(3)如图3,小明先在原矩形硬纸片的两个角各剪去一个同样大小的正方形(阴影部分),经过思考他发现,再剪去两个同样大小的矩形后,可将剩余部分折成一个有盖纸盒。若折成的有盖长方体纸盒的表面积为$412cm^2,$请计算剪去的正方形的边长。
答案:解析 (1) $26$;$12$。
(2) 设剪去的小正方形的边长为$x\text{cm}$,
根据题意,得$(30 - 2x)(16 - 2x) = 240$,
解得$x_1 = 20$(不符合题意,舍去),$x_2 = 3$。
答:剪去的小正方形的边长为$3\text{cm}$。
(3) 设剪去的正方形的边长为$y\text{cm}$,
根据题意,得剪去的矩形的长为$\frac{30}{2} = 15\text{cm}$,宽为$y\text{cm}$,
∴$30×16 - 2y^2 - 2×15y = 412$,
解得$y_1 = -17$(不符合题意,舍去),$y_2 = 2$。
答:剪去的正方形的边长为$2\text{cm}$。
(2) 设剪去的小正方形的边长为$x\text{cm}$,
根据题意,得$(30 - 2x)(16 - 2x) = 240$,
解得$x_1 = 20$(不符合题意,舍去),$x_2 = 3$。
答:剪去的小正方形的边长为$3\text{cm}$。
(3) 设剪去的正方形的边长为$y\text{cm}$,
根据题意,得剪去的矩形的长为$\frac{30}{2} = 15\text{cm}$,宽为$y\text{cm}$,
∴$30×16 - 2y^2 - 2×15y = 412$,
解得$y_1 = -17$(不符合题意,舍去),$y_2 = 2$。
答:剪去的正方形的边长为$2\text{cm}$。
例题 「2025福建福州平潭月考」如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙足够长),另三边用木栏围成,木栏长40m,当AB长为

10
米时,鸡场的面积为$200m^2。$
答案:答案 $10$
解析 设$AB = x\text{m}$,则$BC = (40 - 2x)\text{m}$,∴$x(40 - 2x) = 200$,解得$x_1 = x_2 = 10$,∴$AB = 10\text{m}$。
解析 设$AB = x\text{m}$,则$BC = (40 - 2x)\text{m}$,∴$x(40 - 2x) = 200$,解得$x_1 = x_2 = 10$,∴$AB = 10\text{m}$。
变式1【无门→单门】「2024内蒙古通辽中考」如图,小程的爸爸用一段10m长的铁丝网围成一个一边靠墙(墙长5.5m)的矩形鸭舍,其面积为$15m^2,$在鸭舍侧面中间位置留一个1m宽的门(由其他材料制成),则BC的长为(

A. 5m或6m
B. 2.5m或3m
C. 5m
D. 3m
C
)
A. 5m或6m
B. 2.5m或3m
C. 5m
D. 3m
答案:C 设$BC = x\text{m}$,则$AB = \frac{1}{2}(10 + 1 - x) = \frac{1}{2}(11 - x)\text{m}$,根据题意,得$\frac{1}{2}(11 - x)x = 15$,解得$x = 5$或$x = 6 > 5.5$(不合题意,舍去),即$BC$的长为$5\text{m}$。故选C。
变式2【无门→双门】如图,用长为20m的篱笆,一面利用墙(墙的最大可用长度为11m),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料做了宽为1m的两扇小门。若花圃的面积刚好为$40m^2,$则此时花圃AB段的长为

4
m。
答案:答案 $4$
解析 设$AB$的长为$x\text{m}$,则$BC$的长为$(20 - 3x + 2)\text{m}$,根据题意,得$x(20 - 3x + 2) = 40$,整理,得$3x^2 - 22x + 40 = 0$,解得$x_1 = \frac{10}{3}$,$x_2 = 4$。当$x = \frac{10}{3}$时,$20 - 3x + 2 = 12 > 11$,不合题意,舍去;当$x = 4$时,$20 - 3x + 2 = 10$,符合题意,∴花圃$AB$段的长为$4\text{m}$。
解析 设$AB$的长为$x\text{m}$,则$BC$的长为$(20 - 3x + 2)\text{m}$,根据题意,得$x(20 - 3x + 2) = 40$,整理,得$3x^2 - 22x + 40 = 0$,解得$x_1 = \frac{10}{3}$,$x_2 = 4$。当$x = \frac{10}{3}$时,$20 - 3x + 2 = 12 > 11$,不合题意,舍去;当$x = 4$时,$20 - 3x + 2 = 10$,符合题意,∴花圃$AB$段的长为$4\text{m}$。