1.「2025 上海徐汇月考」下列方程中,是一元二次方程的为 (
A. $x+\frac{1}{x}= 2$
B. $a x^{2}+b x+c= 0$
C. $x(x+2)= x(x-1)$
D. $2 x^{2}= 5 x-7$
D
)A. $x+\frac{1}{x}= 2$
B. $a x^{2}+b x+c= 0$
C. $x(x+2)= x(x-1)$
D. $2 x^{2}= 5 x-7$
答案:D $A. x+\frac{1}{x}=2$ 是分式方程;B. 当 $a \neq 0$,且 $a$、$b$、$c$ 为常数时,$a x^{2}+b x+c=0$ 是一元二次方程;C. $x(x+2)=x(x-1)$ 整理后为 $3 x=0$,是一元一次方程;D. $2 x^{2}=5 x-7$ 是关于 $x$ 的一元二次方程. 故选 D.
2.「2025 重庆开州月考」用配方法将一元二次方程 $x^{2}+4 x-1= 0$ 变形,结果正确的是 (
A. $(x+2)^{2}= 3$
B. $(x-2)^{2}= 5$
C. $(x+2)^{2}= 5$
D. $(x-2)^{2}= 3$
C
)A. $(x+2)^{2}= 3$
B. $(x-2)^{2}= 5$
C. $(x+2)^{2}= 5$
D. $(x-2)^{2}= 3$
答案:C 原方程移项得 $x^{2}+4 x=1, \therefore x^{2}+4 x+4=1+4$,即 $(x+2)^{2}=5$. 故选 C.
3.「2025 河北保定曲阳期中」已知 $m$ 是方程 $x^{2}-2 x-2020= 0$ 的一个根,则 $2 m^{2}-4 m$ 的值是 (
A. 2020
B. -2020
C. -4040
D. 4040
D
)A. 2020
B. -2020
C. -4040
D. 4040
答案:D $\because m$ 是方程 $x^{2}-2 x-2020=0$ 的一个根,$\therefore m^{2}-2 m-2020=0, \therefore m^{2}-2 m=2020, \therefore 2 m^{2}-4 m=2\left(m^{2}-2 m\right)=2 \times 2020=4040$. 故选 D.
4.「2024 吉林中考」下列方程中,有两个相等实数根的是 (
A. $(x-2)^{2}= -1$
B. $(x-2)^{2}= 0$
C. $(x-2)^{2}= 1$
D. $(x-2)^{2}= 2$
B
)A. $(x-2)^{2}= -1$
B. $(x-2)^{2}= 0$
C. $(x-2)^{2}= 1$
D. $(x-2)^{2}= 2$
答案:B $A. \because-1<0, \therefore$ 方程 $(x-2)^{2}=-1$ 没有实数根;B. $\because(x-2)^{2}=0, \therefore x_{1}=x_{2}=2, \therefore$ 此方程有两个相等的实数根;C. $\because 1>0, \therefore$ 方程 $(x-2)^{2}=1$ 有两个不相等的实数根;D. $\because 2>0, \therefore$ 方程 $(x-2)^{2}=2$ 有两个不相等的实数根. 故选 B.
5.「2024 云南中考」两年前生产 1 千克甲种药品的成本为 80 元,随着生产技术的进步,现在生产 1 千克甲种药品的成本为 60 元.设甲种药品成本的年平均下降率为 $x$,根据题意,下列方程正确的是 (
A. $80\left(1-x^{2}\right)= 60$
B. $80(1-x)^{2}= 60$
C. $80(1-x)= 60$
D. $80(1-2 x)= 60$
B
)A. $80\left(1-x^{2}\right)= 60$
B. $80(1-x)^{2}= 60$
C. $80(1-x)= 60$
D. $80(1-2 x)= 60$
答案:B 两年前生产 1 千克甲种药品的成本为 80 元,甲种药品成本的年平均下降率为 $x$,则去年生产 1 千克甲种药品的成本为 $80(1-x)$ 元,现在生产 1 千克甲种药品的成本为 $80(1-x)^{2}$ 元,已知现在的成本为 60 元,则可得方程为 $80(1-x)^{2}=60$. 故选 B.
6.「2025 湖南岳阳月考」若菱形两条对角线的长度是方程 $x^{2}-8 x+12= 0$ 的两根,则该菱形的边长为 (
A. $\sqrt{10}$
B. 4
C. $2 \sqrt{10}$
D. 5
A
)A. $\sqrt{10}$
B. 4
C. $2 \sqrt{10}$
D. 5
答案:A $\because x^{2}-8 x+12=0, \therefore(x-6)(x-2)=0$,解得 $x_{1}=6$,$x_{2}=2, \because$ 菱形两条对角线的长度是方程 $x^{2}-8 x+12=0$ 的两根,$\therefore$ 菱形两条对角线的长度为 $2,6, \therefore$ 菱形的边长 $=\sqrt{\left(\frac{2}{2}\right)^{2}+\left(\frac{6}{2}\right)^{2}}=\sqrt{1^{2}+3^{2}}=\sqrt{10}$. 故选 A.
7. 若 $x^{2}-2 x-2= \left(x^{2}-4 x+3\right)^{0}$, 则 $x$ 的值为 (
A. -1
B. 3
C. 1
D. 3 或 -1
A
)A. -1
B. 3
C. 1
D. 3 或 -1
答案:A $\because x^{2}-2 x-2=\left(x^{2}-4 x+3\right)^{0}, \therefore x^{2}-2 x-2=1, x^{2}-4 x+3 \neq 0$. 由 $x^{2}-2 x-2=1$ 整理得 $x^{2}-2 x-3=0, \therefore(x-3)(x+1)=0, \therefore x=3$ 或 $x=-1$;由 $x^{2}-4 x+3 \neq 0$ 可知 $(x-3) \cdot(x-1) \neq 0, \therefore x \neq 3$ 且 $x \neq 1, \therefore x$ 的值为 -1. 故选 A.
易错点 易忽视 0 次幂的底数不为 0.
易错点 易忽视 0 次幂的底数不为 0.
8. 学科教材变式「2025 山东济宁金乡月考」如图所示,某市世纪广场有一块长 18 m,宽 15 m 的长方形绿地,在绿地中开辟三条道路后剩余绿地的面积为 $224 \mathrm{~m}^{2}$, 则图中 $x$ 的值为 (
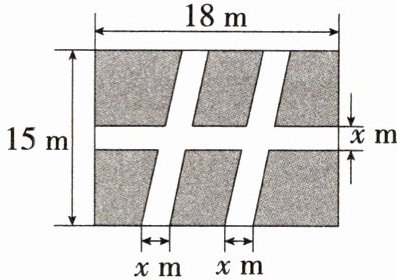
A. 1
B. 2
C. 3
D. 4
A
)
A. 1
B. 2
C. 3
D. 4
答案:A 根据题意,得剩余绿地可看成长为 $(18-2 x) \mathrm{m}$,宽为 $(15-x) \mathrm{m}$ 的长方形,$\therefore(18-2 x)(15-x)=224$,整理得 $x^{2}-24 x+23=0$,解得 $x_{1}=1, x_{2}=23$ (不符合题意,舍去),$\therefore$ 题图中 $x$ 的值为 1. 故选 A.
9.「2024 河南中考」若关于 $x$ 的方程 $\frac{1}{2} x^{2}-x+c= 0$ 有两个相等的实数根,则 $c$ 的值为____
$\frac{1}{2}$
.答案:答案 $\frac{1}{2}$
解析 因为关于 $x$ 的方程 $\frac{1}{2} x^{2}-x+c=0$ 有两个相等的实数根,所以 $\Delta=(-1)^{2}-4 \times \frac{1}{2} c=0$,解得 $c=\frac{1}{2}$.
解析 因为关于 $x$ 的方程 $\frac{1}{2} x^{2}-x+c=0$ 有两个相等的实数根,所以 $\Delta=(-1)^{2}-4 \times \frac{1}{2} c=0$,解得 $c=\frac{1}{2}$.
10.「2024 江苏无锡梁溪期中」若关于 $x$ 的一元二次方程 $(m-1) x^{2}+5 x+m^{2}-3 m+2= 0$ 的常数项为 0,则 $m$ 的值为
2
.答案:答案 2
解析 根据题意,得 $m^{2}-3 m+2=0$ 且 $m-1 \neq 0$,解得 $m=2$.
解析 根据题意,得 $m^{2}-3 m+2=0$ 且 $m-1 \neq 0$,解得 $m=2$.
11.「2024 山东烟台中考」若一元二次方程 $2 x^{2}-4 x-1= 0$ 的两根为 $m, n$, 则 $3 m^{2}-4 m+n^{2}$ 的值为____
6
.答案:答案 6
解析 $\because$ 一元二次方程 $2 x^{2}-4 x-1=0$ 的两根为 $m, n$,$\therefore 2 m^{2}-4 m=1, m+n=-\frac{-4}{2}=2, m n=-\frac{1}{2}, \therefore 3 m^{2}-4 m+n^{2}=2 m^{2}-4 m+m^{2}+n^{2}=1+(m+n)^{2}-2 m n=1+2^{2}-2 \times\left(-\frac{1}{2}\right)=6$.
解析 $\because$ 一元二次方程 $2 x^{2}-4 x-1=0$ 的两根为 $m, n$,$\therefore 2 m^{2}-4 m=1, m+n=-\frac{-4}{2}=2, m n=-\frac{1}{2}, \therefore 3 m^{2}-4 m+n^{2}=2 m^{2}-4 m+m^{2}+n^{2}=1+(m+n)^{2}-2 m n=1+2^{2}-2 \times\left(-\frac{1}{2}\right)=6$.
12.「2024 四川凉山州中考」已知 $y^{2}-x= 0, x^{2}-3 y^{2}+x-3= 0$, 则 $x$ 的值为
3
.答案:答案 3
解析 $\because y^{2}-x=0, \therefore y^{2}=x \geqslant 0, \because x^{2}-3 y^{2}+x-3=0$,$\therefore x^{2}-3 x+x-3=0$,即 $x^{2}-2 x-3=0$,解得 $x_{1}=3, x_{2}=-1$ (舍去),即 $x$ 的值为 3.
易错点 易忽略隐藏条件 $x=y^{2} \geqslant 0$.
解析 $\because y^{2}-x=0, \therefore y^{2}=x \geqslant 0, \because x^{2}-3 y^{2}+x-3=0$,$\therefore x^{2}-3 x+x-3=0$,即 $x^{2}-2 x-3=0$,解得 $x_{1}=3, x_{2}=-1$ (舍去),即 $x$ 的值为 3.
易错点 易忽略隐藏条件 $x=y^{2} \geqslant 0$.
13. (12 分) 解下列方程:
(1) $2 x^{2}-4 x+1= 0$.
(2) $x^{2}+2 x-2= 0$.
(3) $x^{2}-x= 2 x-2$.
(4) $(x-2)^{2}= (2 x-1)(x-2)$.
(1) $2 x^{2}-4 x+1= 0$.
$\because a=2, b=-4, c=1, \therefore \Delta=b^{2}-4 a c=(-4)^{2}-4 × 2 × 1=8, \therefore$ 该方程有两个不相等的实数根,$\therefore x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}=\frac{4 \pm 2 \sqrt{2}}{4}=1 \pm \frac{\sqrt{2}}{2}, \therefore x_{1}=1+\frac{\sqrt{2}}{2}$,$x_{2}=1-\frac{\sqrt{2}}{2}$
(2) $x^{2}+2 x-2= 0$.
移项,得 $x^{2}+2 x=2$,配方,得 $x^{2}+2 x+1=2+1$,即 $(x+1)^{2}=3$,直接开平方,得 $x+1= \pm \sqrt{3}, \therefore x_{1}=-1+\sqrt{3}, x_{2}=-1-\sqrt{3}$
(3) $x^{2}-x= 2 x-2$.
整理,得 $x(x-1)-2(x-1)=0$,因式分解,得 $(x-2)(x-1)=0$,$\therefore x-2=0$ 或 $x-1=0, \therefore x_{1}=2, x_{2}=1$
(4) $(x-2)^{2}= (2 x-1)(x-2)$.
移项,得 $(x-2)^{2}-(2 x-1)(x-2)=0$,因式分解,得 $(x-2)[(x-2)-(2 x-1)]=0$,即 $(x-2)(-x-1)=0$,$\therefore x-2=0$ 或 $-x-1=0, \therefore x_{1}=2, x_{2}=-1$
答案:解析 (1) $\because a=2, b=-4, c=1, \therefore \Delta=b^{2}-4 a c=(-4)^{2}-4 \times 2 \times 1=8, \therefore$ 该方程有两个不相等的实数根,$\therefore x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}=\frac{4 \pm 2 \sqrt{2}}{4}=1 \pm \frac{\sqrt{2}}{2}, \therefore x_{1}=1+\frac{\sqrt{2}}{2}$,$x_{2}=1-\frac{\sqrt{2}}{2}$.
(2) 移项,得 $x^{2}+2 x=2$,配方,得 $x^{2}+2 x+1=2+1$,即 $(x+1)^{2}=3$,直接开平方,得 $x+1= \pm \sqrt{3}, \therefore x_{1}=-1+\sqrt{3}, x_{2}=-1-\sqrt{3}$.
(3) 整理,得 $x(x-1)-2(x-1)=0$,因式分解,得 $(x-2)(x-1)=0$,$\therefore x-2=0$ 或 $x-1=0, \therefore x_{1}=2, x_{2}=1$.
(4) 移项,得 $(x-2)^{2}-(2 x-1)(x-2)=0$,因式分解,得 $(x-2)[(x-2)-(2 x-1)]=0$,即 $(x-2)(x+1)=0$,$\therefore x-2=0$ 或 $x+1=0, \therefore x_{1}=2, x_{2}=-1$.
(2) 移项,得 $x^{2}+2 x=2$,配方,得 $x^{2}+2 x+1=2+1$,即 $(x+1)^{2}=3$,直接开平方,得 $x+1= \pm \sqrt{3}, \therefore x_{1}=-1+\sqrt{3}, x_{2}=-1-\sqrt{3}$.
(3) 整理,得 $x(x-1)-2(x-1)=0$,因式分解,得 $(x-2)(x-1)=0$,$\therefore x-2=0$ 或 $x-1=0, \therefore x_{1}=2, x_{2}=1$.
(4) 移项,得 $(x-2)^{2}-(2 x-1)(x-2)=0$,因式分解,得 $(x-2)[(x-2)-(2 x-1)]=0$,即 $(x-2)(x+1)=0$,$\therefore x-2=0$ 或 $x+1=0, \therefore x_{1}=2, x_{2}=-1$.