9.「2025 北京第一六六中学期中, ★☆」用绳子围成周长为 10 m 的矩形, 记矩形的一边长为 $ x $ m, 它的邻边长为 $ y $ m, 矩形的面积为 $ S $ $ m^{2} $, 当 $ x $ 在一定范围内变化时, $ y $ 和 $ S $ 都随 $ x $ 的变化而变化, 则 $ y $ 与 $ x $、$ S $ 与 $ x $ 满足的函数关系分别是 (
A. 一次函数关系、二次函数关系
B. 正比例函数关系、二次函数关系
C. 二次函数关系、一次函数关系
D. 正比例函数关系、一次函数关系
A
)A. 一次函数关系、二次函数关系
B. 正比例函数关系、二次函数关系
C. 二次函数关系、一次函数关系
D. 正比例函数关系、一次函数关系
答案:A
10.「2025 福建福州闽侯期中, ★☆」某商品每件进价为 20 元, 销售期间发现, 当每件商品的售价为 25 元时, 每天可售出 120 件, 销售单价每降低 1 元, 每天销量增加 10 件, 现商家决定降价销售, 每件降价 $ x $ 元 ($ 0 < x < 5 $), 设每天的销售量为 $ y $ 件, 每天销售该商品获得的利润为 $ w $ 元, 则下列函数关系式正确的是 (
A. $ y = 10x - 120 $
B. $ y = -10x + 120 $
C. $ w = (10x + 120)(25 - 20 - x) $
D. $ w = (-10x + 120)(50 - x) $
C
)A. $ y = 10x - 120 $
B. $ y = -10x + 120 $
C. $ w = (10x + 120)(25 - 20 - x) $
D. $ w = (-10x + 120)(50 - x) $
答案:C
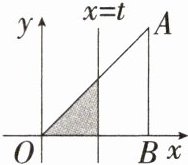
11.「2024 山东德州宁津月考, ★☆」如图, 在 $ Rt\triangle AOB $ 中, $ AB \perp OB $, 且 $ AB = OB = 3 $, 设直线 $ x = t $ ($ 0 < t < 3 $) 截此三角形所得阴影部分的面积为 $ S $, 则 $ S $ 与 $ t $ 之间的函数关系式为 (
A. $ S = t $
B. $ S = \frac{1}{2}t^{2} $
C. $ S = t^{2} $
D. $ S = \frac{1}{2}t^{2} - 1 $
B
)
A. $ S = t $
B. $ S = \frac{1}{2}t^{2} $
C. $ S = t^{2} $
D. $ S = \frac{1}{2}t^{2} - 1 $
答案:答案 B
解析 由题意可知,阴影部分为等腰直角三角形,其直角边长为 $ t $,根据三角形面积公式可得 $ S = \frac{1}{2}t^{2}(0\lt t\lt3)$,即$S=\frac {1}{2}t^{2}(0\lt t\lt3)$。故选 B。
解析 由题意可知,阴影部分为等腰直角三角形,其直角边长为 $ t $,根据三角形面积公式可得 $ S = \frac{1}{2}t^{2}(0\lt t\lt3)$,即$S=\frac {1}{2}t^{2}(0\lt t\lt3)$。故选 B。
12. 学科 易错题「2025 山东德州齐河月考, ★☆」若函数 $ y = (m^{2} + m)x^{m^{2} - 2m - 1} $ 是关于 $ x $ 的二次函数, 则 $ m $ 的值是
3
.答案:答案 3
解析 由$y=(m^{2}+m)x^{m^{2}-2m-1}$是关于 x 的二次函数,得$m^{2}-2m-1=2$且$m^{2}+m≠0$,解得$m=3$。
易错点 易忽视二次项系数不为 0 的隐含条件。
解析 由$y=(m^{2}+m)x^{m^{2}-2m-1}$是关于 x 的二次函数,得$m^{2}-2m-1=2$且$m^{2}+m≠0$,解得$m=3$。
易错点 易忽视二次项系数不为 0 的隐含条件。
13.「2025 广东珠海香洲期中, ★☆」如图, 正方形 $ EFGH $ 的四个顶点分别在边长为 2 的正方形 $ ABCD $ 的四条边上. 若设 $ AE = x $, 正方形 $ EFGH $ 的面积为 $ y $, 求 $ y $ 与 $ x $ 的函数解析式.


答案:
解析 如图所示:
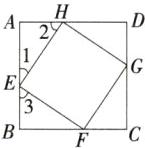
∵ 四边形 ABCD 是边长为 2 的正方形,
$\therefore ∠A=∠B=90^{\circ },AB=2,\therefore ∠1+∠2=90^{\circ }$。
∵ 四边形 EFGH 为正方形,$\therefore ∠HEF=90^{\circ },EH=EF$,
$\therefore ∠1+∠3=90^{\circ },\therefore ∠2=∠3$。
在$\triangle AHE$与$\triangle BEF$中,$\left\{\begin{array}{l} ∠A=∠B,\\ ∠2=∠3,\\ EH=FE,\end{array}\right.$
$\therefore \triangle AHE\cong \triangle BEF(AAS),\therefore AE=BF=x,AH=BE=2 - x$。在$Rt\triangle AHE$中,由勾股定理得$EH^{2}=AE^{2}+AH^{2}=x^{2}+(2 - x)^{2}=2x^{2}-4x + 4$,$\therefore y=2x^{2}-4x + 4(0\leq x\leq2)$。
解析 如图所示:

∵ 四边形 ABCD 是边长为 2 的正方形,
$\therefore ∠A=∠B=90^{\circ },AB=2,\therefore ∠1+∠2=90^{\circ }$。
∵ 四边形 EFGH 为正方形,$\therefore ∠HEF=90^{\circ },EH=EF$,
$\therefore ∠1+∠3=90^{\circ },\therefore ∠2=∠3$。
在$\triangle AHE$与$\triangle BEF$中,$\left\{\begin{array}{l} ∠A=∠B,\\ ∠2=∠3,\\ EH=FE,\end{array}\right.$
$\therefore \triangle AHE\cong \triangle BEF(AAS),\therefore AE=BF=x,AH=BE=2 - x$。在$Rt\triangle AHE$中,由勾股定理得$EH^{2}=AE^{2}+AH^{2}=x^{2}+(2 - x)^{2}=2x^{2}-4x + 4$,$\therefore y=2x^{2}-4x + 4(0\leq x\leq2)$。
14. 新课标 推理能力 新 规律探究题 如图, 用同样规格的黑、白两色正方形瓷砖铺设矩形地面, 请观察图形并解答下列问题.

(1) 在第 $ n $ 个图形中, 每一横行共有
(2) 设铺设地面所用瓷砖的总块数为 $ y $, 请写出 $ y $ 与 $ n $ 的函数关系式.
(3) 按上述铺设方案, 铺一块这样的矩形地面共用了 106 块黑色瓷砖, 求白色瓷砖共用多少块.

(1) 在第 $ n $ 个图形中, 每一横行共有
$n+3$
块瓷砖, 每一竖列共有$n+2$
块瓷砖. (均用含 $ n $ 的代数式表示)(2) 设铺设地面所用瓷砖的总块数为 $ y $, 请写出 $ y $ 与 $ n $ 的函数关系式.
$y=n^{2}+5n + 6$
(3) 按上述铺设方案, 铺一块这样的矩形地面共用了 106 块黑色瓷砖, 求白色瓷砖共用多少块.
650
答案:解析 (1)$(n + 3);(n + 2)$。
(2) 由(1)得,y 与 n 的函数关系式是$y=(n + 2)(n + 3)=n^{2}+5n + 6$。
(3) 由题图可得,第 n 个图形中白色瓷砖有$[n(n + 1)]$块,则黑色瓷砖有$(n^{2}+5n + 6)-n(n + 1)=(4n + 6)$块。当$4n + 6 = 106$时,$n = 25$,则白色瓷砖有$n(n + 1)=650$(块)。
(2) 由(1)得,y 与 n 的函数关系式是$y=(n + 2)(n + 3)=n^{2}+5n + 6$。
(3) 由题图可得,第 n 个图形中白色瓷砖有$[n(n + 1)]$块,则黑色瓷砖有$(n^{2}+5n + 6)-n(n + 1)=(4n + 6)$块。当$4n + 6 = 106$时,$n = 25$,则白色瓷砖有$n(n + 1)=650$(块)。