1.「2025 湖北荆州沙市期中」下列函数中属于二次函数的是 ()
A. $ y = x(x + 1) $
B. $ x^{2}y = 1 $
C. $ y = 2x^{2} - 2(x^{2} + 1) $
D. $ y = ax^{2} + bx + c $

2.「2025 浙江金华义乌期中」二次函数 $ y = 2x^{2} - 1 $ 的二次项系数、一次项系数、常数项分别为 ()
A. 2,0,-1
B. 2,2,-1
C. 2,2,1
D. 2,0,1

3. 函数 $ y = (m^{2} - 10)x^{2} + 3x - 5m $ 是二次函数的条件是 ()
A. $ m \neq 0 $
B. $ m \neq 10 $
C. $ m \neq \sqrt{10} $
D. $ m \neq \sqrt{10} $ 且 $ m \neq -\sqrt{10} $

4. 已知二次函数 $ y = (2x + 3)(x - 1) + 5 $ 的二次项系数、一次项系数、常数项分别为 $ a,b,c $, 则 $ a - b + c = $.

5.「2025 江西南昌青山湖月考」已知函数 $ y = (m^{2} + 2m)x^{2} + mx + m + 1 $.
(1) 当 $ m $ 为何值时, 此函数是一次函数?
(2) 当 $ m $ 为何值时, 此函数是二次函数?

6.「2025 浙江宁波镇海期中」红光公司 2024 年 7 月份生产儿童玩具 20 万件, 计划之后的两个月增加产量, 如果月平均增长率为 $ x $, 那么第三季度儿童玩具的产量 $ y $ (万件) 与 $ x $ 之间的关系应表示为 ()
A. $ y = 20(1 + x) $
B. $ y = 20(1 - x)^{2} $
C. $ y = 20(1 + x)^{2} $
D. $ y = 20 + 20(x + 1) + 20(x + 1)^{2} $

7.「2025 山东济南莱芜期中」某农户想要用栅栏围成一个长方形养鸡场, 如图所示, 养鸡场的一边靠墙, 另外三边用栅栏围成, 若栅栏的总长为 10 米, 设长方形垂直于墙的一边长为 $ x $ 米, 面积为 $ y $ 平方米, 则 $ y $ 与 $ x $ 之间满足的函数关系式是 ()
A. $ y = 10x $
B. $ y = 10 - 2x $
C. $ y = \frac{10}{x} $
D. $ y = -2x^{2} + 10x $

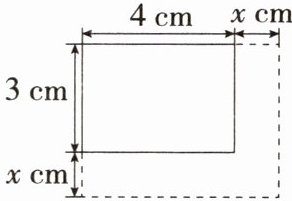
8. 学科 教材变式 如图, 矩形的长是 4 cm, 宽是 3 cm, 如果将其长与宽各增加 $ x $ cm, 那么面积增加 $ y $ $ cm^{2} $.
(1) 写出 $ y $ 与 $ x $ 的函数关系式.
(2) $ y $ 是 $ x $ 的什么函数?
(3) 自变量 $ x $ 的取值范围是什么?