1.「2025北京东城期中」对于二次函数$y= -2(x+1)^{2}$,下列说法错误的是(
A. 它的图象的开口向下
B. 它的图象的对称轴是直线$x= 1$
C. 当$x= -1$时,$y$取最大值
D. 当$x＞1$时,$y随x$的增大而减小
B
)A. 它的图象的开口向下
B. 它的图象的对称轴是直线$x= 1$
C. 当$x= -1$时,$y$取最大值
D. 当$x＞1$时,$y随x$的增大而减小
答案：B 对于二次函数y=−2(x+1)²，∵−2＜0，∴它的图象开口向下，故A正确；对称轴为直线x=−1，故B错误；当x=−1时，y有最大值，故C正确；∵当x＞−1时，y随x的增大而减小，∴当x＞1时，y随x的增大而减小，故D正确。故选B。
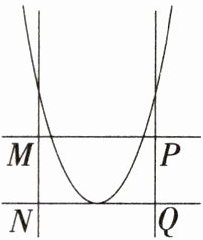
2. 新课标 几何直观 若二次函数$y= 2(x-1)^{2}$的图象如图所示,则坐标原点可能是(
A. 点$M$
B. 点$N$
C. 点$P$
D. 点$Q$
B
)A. 点$M$
B. 点$N$
C. 点$P$
D. 点$Q$
答案：B ∵y=2(x−1)²，∴抛物线的顶点坐标为(1,0)，∴坐标原点可能是点N。故选B。
3.「2025北京海淀期中」已知函数$y= -(x-2)^{2}$的图象上有A(-$\frac {1}{2},y_{1}),B(1,y_{2}),C(5,y_{3})$三点,则$y_{1},y_{2},y_{3}$的大小关系是____
y3＜y1＜y2
(用“＜”连接)。答案：答案y3＜y1＜y2
解析 当x= -$\frac{1}{2}$时，y1=−( -$\frac{1}{2}$ - 2)²= -$\frac{25}{4}$；当x=1时，y2=−(1−2)²=−1；当x=5时，y3=−(5−2)²=−9。
∵−9＜ -$\frac{25}{4}$＜−1，∴y3＜y1＜y2。
解析 当x= -$\frac{1}{2}$时，y1=−( -$\frac{1}{2}$ - 2)²= -$\frac{25}{4}$；当x=1时，y2=−(1−2)²=−1；当x=5时，y3=−(5−2)²=−9。
∵−9＜ -$\frac{25}{4}$＜−1，∴y3＜y1＜y2。
4.「2025北京东城期中」二次函数$y= 2(x-1)^{2}$的图象可以由函数$y= 2x^{2}$的图象向
右
平移1
个单位得到。答案：答案 右；1
解析 根据二次函数图象的平移规律“左加右减自变量，上加下减常数项”可知，函数y=2(x−1)²的图象可以由函数y=2x²的图象向右平移1个单位得到。
解析 根据二次函数图象的平移规律“左加右减自变量，上加下减常数项”可知，函数y=2(x−1)²的图象可以由函数y=2x²的图象向右平移1个单位得到。
5. 已知抛物线$y= -3x^{2}$,若抛物线不动,把$y$轴向右平移3个单位,则在新坐标系下抛物线的解析式为
y=−3(x+3)²
。答案：答案y=−3(x+3)²
解析 抛物线y=−3x²的顶点坐标为(0,0)，∵把y轴向右平移3个单位，∴新平面直角坐标系中抛物线的顶点坐标为(−3,0)，∴新坐标系下抛物线的解析式是y=−3(x+3)²。
解析 抛物线y=−3x²的顶点坐标为(0,0)，∵把y轴向右平移3个单位，∴新平面直角坐标系中抛物线的顶点坐标为(−3,0)，∴新坐标系下抛物线的解析式是y=−3(x+3)²。
6.「2025云南昆明期末,★☆」在同一平面直角坐标系中,一次函数$y= ax+c和二次函数y= a(x+c)^{2}$的图象大致为(
B
)答案：B A. 由题中图象可知，函数y=ax+c中，a＞0，c＞0，函数y=a(x+c)²中，a＜0，c＜0，矛盾，故A错误；B. 由题中图象可知，函数y=ax+c中，a＜0，c＞0，函数y=a(x+c)²中，a＜0，c＞0，一致，故B正确；C. 由题中图象可知，函数y=ax+c中，a＞0，c＜0，函数y=a(x+c)²中，a＞0，c＞0，矛盾，故C错误；D. 由题中图象可知，函数y=ax+c中，a＜0，c＞0，函数y=a(x+c)²中，a＞0，c＜0，矛盾，故D错误。故选B。
7.「2024福建莆田荔城开学测试,★☆」已知抛物线$y= a(x-h)^{2}$,当$x= 2$时,有最大值,且抛物线过点$(1,-3)$。
(1)求抛物线的解析式。
解：抛物线的解析式为
(2)当$0＜x＜5$时,写出$y$的取值范围。
解：$y$的取值范围为
(1)求抛物线的解析式。
解：抛物线的解析式为
$y=-3(x-2)^2$
。(2)当$0＜x＜5$时,写出$y$的取值范围。
解：$y$的取值范围为
$-27＜y≤0$
。答案：解析 (1) ∵抛物线y=a(x−h)²，当x=2时，有最大值，∴抛物线的解析式为y=a(x−2)²，
∵抛物线过点(1,−3)，∴−3=a(1−2)²，解得a=−3，
∴此抛物线的解析式为y=−3(x−2)²。
(2) ∵抛物线的对称轴为直线x=2，抛物线开口向下，
∴当0＜x≤2时，y随x的增大而增大，当2＜x＜5时，y随x的增大而减小，∴当x=2时，y取最大值，为0，
∵|0 - 2|＜|5 - 2|，且当x=5时，y=−27，
∴当0＜x＜5时，y的取值范围为−27＜y≤0。
∵抛物线过点(1,−3)，∴−3=a(1−2)²，解得a=−3，
∴此抛物线的解析式为y=−3(x−2)²。
(2) ∵抛物线的对称轴为直线x=2，抛物线开口向下，
∴当0＜x≤2时，y随x的增大而增大，当2＜x＜5时，y随x的增大而减小，∴当x=2时，y取最大值，为0，
∵|0 - 2|＜|5 - 2|，且当x=5时，y=−27，
∴当0＜x＜5时，y的取值范围为−27＜y≤0。
8.「2023辽宁鞍山海城期中,★☆」如图,抛物线$y= a(x+1)^{2}的顶点为A$,与$y轴的负半轴交于点B$,且$S_{\triangle AOB}= \frac {1}{2}$。
(1)求抛物线的解析式。
(2)若点$C是该抛物线上A$、$B$两点之间的一动点,求$\triangle ABC$面积的最大值。
(1)求抛物线的解析式。
(2)若点$C是该抛物线上A$、$B$两点之间的一动点,求$\triangle ABC$面积的最大值。
答案：
解析 (1) 根据题意，得A(−1,0)，B(0,a)，a＜0，
∴OA=1，OB= -a，∵S△AOB = $\frac{1}{2}$，∴$\frac{1}{2}$×1×( -a) = $\frac{1}{2}$，解得a=−1，∴抛物线的解析式为y=−(x+1)²。
(2) ∵A(−1,0)，B(0,−1)，
∴直线AB的解析式为y=−x−1，如图，过C作x轴的垂线，
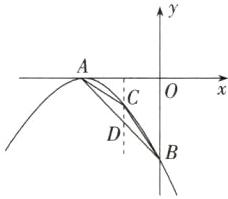交直线AB于点D，设C(x,−(x+1)²)，则D(x,−x−1)，其中−1＜x＜0，∴CD=−(x+1)² + x + 1，∵S△ABC = S△ACD + S△BCD = $\frac{1}{2}$[−(x+1)² + x + 1]×1 = -$\frac{1}{2}$(x + $\frac{1}{2}$)² + $\frac{1}{8}$，∵ -$\frac{1}{2}$＜0，−1＜x＜0，∴△ABC面积的最大值是$\frac{1}{8}$。
解析 (1) 根据题意，得A(−1,0)，B(0,a)，a＜0，
∴OA=1，OB= -a，∵S△AOB = $\frac{1}{2}$，∴$\frac{1}{2}$×1×( -a) = $\frac{1}{2}$，解得a=−1，∴抛物线的解析式为y=−(x+1)²。
(2) ∵A(−1,0)，B(0,−1)，
∴直线AB的解析式为y=−x−1，如图，过C作x轴的垂线，
交直线AB于点D，设C(x,−(x+1)²)，则D(x,−x−1)，其中−1＜x＜0，∴CD=−(x+1)² + x + 1，∵S△ABC = S△ACD + S△BCD = $\frac{1}{2}$[−(x+1)² + x + 1]×1 = -$\frac{1}{2}$(x + $\frac{1}{2}$)² + $\frac{1}{8}$，∵ -$\frac{1}{2}$＜0，−1＜x＜0，∴△ABC面积的最大值是$\frac{1}{8}$。