1.「2025山东滨州滨城期中」关于抛物线$y = - 2(x + 1)^2 + 3$,下列说法错误的是(
A. 开口向下
B. 当$x < - 1$时,$y随x$的增大而减小
C. 对称轴是直线$x = - 1$
D. 经过点$(0,1)$
B
)A. 开口向下
B. 当$x < - 1$时,$y随x$的增大而减小
C. 对称轴是直线$x = - 1$
D. 经过点$(0,1)$
答案:B A. $\because - 2 < 0$,$\therefore$ 抛物线开口向下,故A选项正确;B. $\because$ 抛物线开口向下,对称轴为直线$x = - 1$,$\therefore$ 当$x < - 1$时,$y$随$x$的增大而增大,故B选项错误;C. 由解析式可知,对称轴为直线$x = - 1$,故C选项正确;D. 令$x = 0$,得$y = - 2×1 + 3 = 1$,$\therefore$ 抛物线经过点$(0,1)$,故D选项正确. 故选B.
2.「2025浙江温州瑞安月考」甲,乙两个二次函数分别为$y_{甲} = (x + 10)^2 + 30$,$y_{乙} = - (x - 20)^2 + 30$,下列叙述正确的是(
A. 当$x = 10$时,$y_{甲}$有最大值30
B. 当$x = 10$时,$y_{甲}$有最小值30
C. 当$x = 20$时,$y_{乙}$有最大值30
D. 当$x = 20$时,$y_{乙}$有最小值-30
C
)A. 当$x = 10$时,$y_{甲}$有最大值30
B. 当$x = 10$时,$y_{甲}$有最小值30
C. 当$x = 20$时,$y_{乙}$有最大值30
D. 当$x = 20$时,$y_{乙}$有最小值-30
答案:C $\because$ 二次函数$y_{甲} = (x + 10)^2 + 30$中,$a = 1 > 0$,$\therefore$ 当$x = - 10$时,$y_{甲}$有最小值30,$\therefore$ A、B选项错误;$\because$ 二次函数$y_{乙} = - (x - 20)^2 + 30$中,$a = - 1 < 0$,$\therefore$ 当$x = 20$时,$y_{乙}$有最大值30,$\therefore$ C选项正确,D选项错误. 故选C.
3.「2024四川凉山州中考」抛物线$y = \frac{2}{3}(x - 1)^2 + c经过(- 2,y_1)$,$(0,y_2)$,$(\frac{5}{2},y_3)$三点,则$y_1$,$y_2$,$y_3$的大小关系正确的是(
A. $y_1 > y_2 > y_3$
B. $y_2 > y_3 > y_1$
C. $y_3 > y_1 > y_2$
D. $y_1 > y_3 > y_2$
D
)A. $y_1 > y_2 > y_3$
B. $y_2 > y_3 > y_1$
C. $y_3 > y_1 > y_2$
D. $y_1 > y_3 > y_2$
答案:D $\because y = \frac{2}{3}(x - 1)^2 + c$,$\therefore$ 抛物线开口向上,对称轴是直线$x = 1$,$\therefore$ 当$x < 1$时,$y$随$x$的增大而减小,$\because (\frac{5}{2},y_3)$关于直线$x = 1$的对称点是$(-\frac{1}{2},y_3)$,$- 2 < - \frac{1}{2} < 0 < 1$,$\therefore y_1 > y_3 > y_2$. 故选D.
4.新代数推理如图,在平面直角坐标系中,有两条位置确定的抛物线,它们的对称轴相同,表达式中的$h$,$k$,$m$,$n$都是常数,则下列关系不正确的是(
A. $h < 0$,$k > 0$
B. $m < 0$,$n > 0$
C. $h = m$
D. $k = n$
D
)A. $h < 0$,$k > 0$
B. $m < 0$,$n > 0$
C. $h = m$
D. $k = n$
答案:根据二次函数的解析式确定两抛物线的顶点坐标分别为$(h,k)$,$(m,n)$,因为它们的对称轴相同,所以$m = h$,由题图知$h < 0$,$k > 0$,$m < 0$,$n > 0$,因为点$(h,k)$在点$(m,n)$的下方,所以$k < n$. 故选D.
5.学科分类讨论思想抛物线$y = (x - a)^2 + a - 1$的顶点一定不在(
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
B
)A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
答案:$\because y = (x - a)^2 + a - 1$,$\therefore$ 该抛物线的顶点坐标为$(a,a - 1)$,当$a > 1$时,$a - 1 > 0$,此时顶点在第一象限,故A不符合题意;当$0 < a < 1$时,$- 1 < a - 1 < 0$,此时顶点在第四象限,故D不符合题意;当$a < 0$时,$a - 1 < 0$,此时顶点在第三象限,故C不符合题意. 故选B.
6.学科多解法「2024山东滨州中考」将抛物线$y = - x^2$先向右平移1个单位长度,再向上平移2个单位长度,则平移后抛物线的顶点坐标为______
(1,2)
。答案:答案 $(1,2)$
解析 【解法一】将抛物线$y = - x^2$先向右平移1个单位长度,再向上平移2个单位长度后,抛物线的解析式为$y = - (x - 1)^2 + 2$,$\therefore$ 顶点坐标为$(1,2)$.
【解法二】平移前抛物线$y = - x^2$的顶点坐标为$(0,0)$,先向右平移1个单位长度,再向上平移2个单位长度,平移后对应顶点的坐标为$(1,2)$.
解析 【解法一】将抛物线$y = - x^2$先向右平移1个单位长度,再向上平移2个单位长度后,抛物线的解析式为$y = - (x - 1)^2 + 2$,$\therefore$ 顶点坐标为$(1,2)$.
【解法二】平移前抛物线$y = - x^2$的顶点坐标为$(0,0)$,先向右平移1个单位长度,再向上平移2个单位长度,平移后对应顶点的坐标为$(1,2)$.
7.「2025浙江杭州期中」若$- 1 \leq x \leq m$时,函数$y = (x - 2)^2 + 1$的最大值为17,则$m = $
6
。答案:答案 6
解析 $\because$ 二次函数$y = (x - 2)^2 + 1$,$\therefore$ 该函数图象开口向上,对称轴为直线$x = 2$.
当$x = 2$时,$y$取得最小值,为1,当$x = - 1$时,$y = (- 1 - 2)^2 + 1 = 10$,$\because$ 当$- 1 \leq x \leq m$时,函数$y = (x - 2)^2 + 1$的最大值为17,$\therefore$ 当$x = m$时,$y$取得最大值,为17,即$(m - 2)^2 + 1 = 17$,解得$m = 6$或$m = - 2$(舍去).
解析 $\because$ 二次函数$y = (x - 2)^2 + 1$,$\therefore$ 该函数图象开口向上,对称轴为直线$x = 2$.
当$x = 2$时,$y$取得最小值,为1,当$x = - 1$时,$y = (- 1 - 2)^2 + 1 = 10$,$\because$ 当$- 1 \leq x \leq m$时,函数$y = (x - 2)^2 + 1$的最大值为17,$\therefore$ 当$x = m$时,$y$取得最大值,为17,即$(m - 2)^2 + 1 = 17$,解得$m = 6$或$m = - 2$(舍去).
8.「2023辽宁大连中山期末」已知抛物线$C_1的解析式为y = x^2 - 2x + 1$,将抛物线$C_1$先向右平移1个单位长度,再向下平移2个单位长度得到抛物线$C_2$。
(1)求抛物线$C_2$的函数关系式。
(2)点$A(a,- 3)是不是抛物线C_2$上的点?请说明理由。
(1)求抛物线$C_2$的函数关系式。
(2)点$A(a,- 3)是不是抛物线C_2$上的点?请说明理由。
答案:解析 (1) $\because$ 抛物线$C_1$的解析式为$y = x^2 - 2x + 1 = (x - 1)^2$,$\therefore$ 抛物线的顶点坐标为$(1,0)$,$\therefore$ 平移后的抛物线的顶点坐标为$(2,- 2)$,$\therefore$ 抛物线$C_2$的解析式为$y = (x - 2)^2 - 2$.
(2) 点$A$不是抛物线$C_2$上的点.
理由:$\because$ 抛物线$C_2$的开口向上,函数有最小值,为$- 2$,$- 3 < - 2$,$\therefore$ 点$A$不是抛物线$C_2$上的点.
(2) 点$A$不是抛物线$C_2$上的点.
理由:$\because$ 抛物线$C_2$的开口向上,函数有最小值,为$- 2$,$- 3 < - 2$,$\therefore$ 点$A$不是抛物线$C_2$上的点.
9.「2025江苏苏州姑苏期中,★☆」二次函数$y = a(x - 3)^2 + c与一次函数y = cx + a$在同一坐标系中的大致图象是(
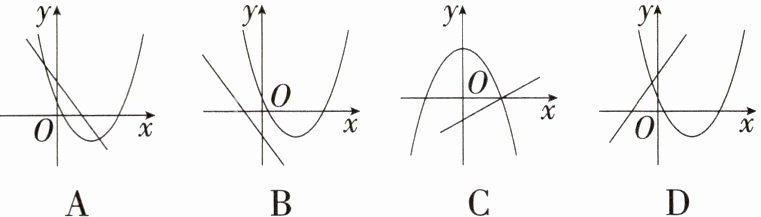
A
)
答案:A. $\because$ 一次函数$y = cx + a$的图象过第一、二、四象限,$\therefore a > 0$,$c < 0$,$\because$ 二次函数$y = a(x - 3)^2 + c$的图象开口向上,顶点$(3,c)$在第四象限,$\therefore a > 0$,$c < 0$,一致,故A正确;B. $\because$ 一次函数$y = cx + a$的图象与$y$轴交于负半轴,$\therefore a < 0$,$\because$ 二次函数$y = a(x - 3)^2 + c$的图象开口向上,$\therefore a > 0$,矛盾,故B错误;C. 二次函数$y = a(x - 3)^2 + c$的对称轴为直线$x = 3$,在$y$轴右侧,故C错误;D. $\because$ 一次函数$y = cx + a$的图象过第一、二、三象限,$\therefore c > 0$,$\because$ 抛物线$y = a(x - 3)^2 + c$的顶点$(3,c)$在第四象限,$\therefore c < 0$,矛盾,故D错误. 故选A.
10.「2025浙江嘉兴平湖林埭中学月考,★☆」已知抛物线$y = - 5(x + m)^2 - 3$。当$x \geq 2$时,$y随x$的增大而减小,那么$m$的取值范围是(
A. $m \geq - 2$
B. $m \leq - 2$
C. $- 2 < m < 0$
D. $m < - 2$
A
)A. $m \geq - 2$
B. $m \leq - 2$
C. $- 2 < m < 0$
D. $m < - 2$
答案:A $\because y = - 5(x + m)^2 - 3$,$\therefore$ 对称轴为直线$x = - m$,$\because a = - 5 < 0$,$\therefore$ 抛物线开口向下,$\therefore$ 在对称轴右侧$y$随$x$的增大而减小,$\because$ 当$x \geq 2$时,$y$随$x$的增大而减小,$\therefore - m \leq 2$,解得$m \geq - 2$,故选A.