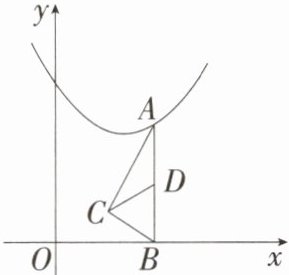
11.「2024吉林临江期末,★☆」如图,在平面直角坐标系中,点$A在抛物线y = (x - 1)^2 + 2$上运动,过点$A作AB \perp x轴于点B$。以$AB为斜边作Rt\triangle ABC$,$AB边上的中线CD$长的最小值是

1
。答案:答案 1
解析 $\because CD$为$Rt\triangle ABC$斜边的中线,$\therefore CD = \frac{1}{2}AB$,又$\because$ 抛物线$y = (x - 1)^2 + 2$的顶点坐标为$(1,2)$,$\therefore$ 点$A$到$x$轴的距离最小为2,$\therefore$ 中线$CD$长的最小值为$\frac{1}{2}×2 = 1$.
方法解读 求动点到直线的距离或求定点到直线的距离的依据是“垂线段最短”,基本构图方法是过点向直线作垂线段,垂线段的长就是所求的距离.
解析 $\because CD$为$Rt\triangle ABC$斜边的中线,$\therefore CD = \frac{1}{2}AB$,又$\because$ 抛物线$y = (x - 1)^2 + 2$的顶点坐标为$(1,2)$,$\therefore$ 点$A$到$x$轴的距离最小为2,$\therefore$ 中线$CD$长的最小值为$\frac{1}{2}×2 = 1$.
方法解读 求动点到直线的距离或求定点到直线的距离的依据是“垂线段最短”,基本构图方法是过点向直线作垂线段,垂线段的长就是所求的距离.
12.「2025河北张家口宣化期中,★☆」杭州亚运会羽毛球比赛项目中,中国队收获4金3银2铜共9枚奖牌。在一次羽毛球比赛中,甲运动员在离地面1米的$A$点处发球,羽毛球的飞行路线为抛物线的一部分。当球运动到最高点时,离甲运动员站立地点$O$的水平距离为4米,其高度为$\frac{21}{5}$米。在离点$O$水平距离5米处,竖直放置一个高1.55米的球网$BC$,以点$O$为原点建立如图所示的直角坐标系,回答下列问题:
(1)求抛物线的解析式(不要求写自变量的取值范围)。
(2)通过计算判断此球能否过网。
(1)求抛物线的解析式(不要求写自变量的取值范围)。
$y = - \frac{1}{5}(x - 4)^2 + \frac{21}{5}$
(2)通过计算判断此球能否过网。
能
答案:解析 (1) 根据题意设抛物线的解析式为$y = a(x - 4)^2 + \frac{21}{5}$,将点$(0,1)$代入可得$1 = a(0 - 4)^2 + \frac{21}{5}$,解得$a = - \frac{1}{5}$,$\therefore$ 抛物线的解析式为$y = - \frac{1}{5}(x - 4)^2 + \frac{21}{5}$.
(2) 此球能过网. 理由如下:
当$x = 5$时,$y = - \frac{1}{5}×(5 - 4)^2 + \frac{21}{5} = 4$,$\because 4 > 1.55$,$\therefore$ 此球能过网.
(2) 此球能过网. 理由如下:
当$x = 5$时,$y = - \frac{1}{5}×(5 - 4)^2 + \frac{21}{5} = 4$,$\because 4 > 1.55$,$\therefore$ 此球能过网.
13.新运算能力学科数形结合思想「2024广东清远模拟」如图,直线$y = x - 3与x$轴、$y轴分别交于点B$、$A$,抛物线$y = a(x - 2)^2 + k经过点A$、$B$,其顶点为$C$。
(1)求抛物线的解析式。
(2)求$\triangle ABC$的面积。
(3)点$P为直线AB$上方抛物线上的任意一点,过点$P作PD // y轴交直线AB于点D$,求线段$PD的最大值及此时点P$的坐标。

(1)求抛物线的解析式。
(2)求$\triangle ABC$的面积。
(3)点$P为直线AB$上方抛物线上的任意一点,过点$P作PD // y轴交直线AB于点D$,求线段$PD的最大值及此时点P$的坐标。

答案:
解析 (1) 当$x = 0$时,$y = - 3$,当$y = 0$时,$x = 3$,$\therefore A(0,- 3)$,$B(3,0)$,把$(0,- 3)$,$(3,0)$代入$y = a(x - 2)^2 + k$,得$\begin{cases}4a + k = - 3\\a + k = 0\end{cases}$,解得$\begin{cases}a = - 1\\k = 1\end{cases}$,$\therefore$ 抛物线的解析式为$y = - (x - 2)^2 + 1 = - x^2 + 4x - 3$.
(2) 由抛物线的顶点式$y = - (x - 2)^2 + 1$得$C(2,1)$,如图,过点$C$作$CQ // y$轴交$AB$于点$Q$,则$Q(2,- 1)$,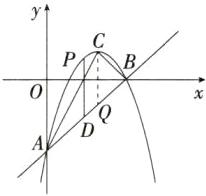
$\therefore S_{\triangle ABC} = S_{\triangle ACQ} + S_{\triangle BCQ} = \frac{1}{2}CQ \cdot OB = \frac{1}{2}×[1 - (- 1)]×3 = 3$.
(3) $\because$ 点$P$为直线$AB$上方抛物线上的任意一点,$\therefore$ 设点$P(x,- x^2 + 4x - 3)(0 < x < 3)$,则$D(x,x - 3)$,$\therefore PD = - x^2 + 4x - 3 - (x - 3) = - x^2 + 3x = - (x - 1.5)^2 + 2.25$,$\therefore$ 当$x = 1.5$时,$PD$有最大值,为$2.25$,此时$P(1.5,0.75)$.
解析 (1) 当$x = 0$时,$y = - 3$,当$y = 0$时,$x = 3$,$\therefore A(0,- 3)$,$B(3,0)$,把$(0,- 3)$,$(3,0)$代入$y = a(x - 2)^2 + k$,得$\begin{cases}4a + k = - 3\\a + k = 0\end{cases}$,解得$\begin{cases}a = - 1\\k = 1\end{cases}$,$\therefore$ 抛物线的解析式为$y = - (x - 2)^2 + 1 = - x^2 + 4x - 3$.
(2) 由抛物线的顶点式$y = - (x - 2)^2 + 1$得$C(2,1)$,如图,过点$C$作$CQ // y$轴交$AB$于点$Q$,则$Q(2,- 1)$,

$\therefore S_{\triangle ABC} = S_{\triangle ACQ} + S_{\triangle BCQ} = \frac{1}{2}CQ \cdot OB = \frac{1}{2}×[1 - (- 1)]×3 = 3$.
(3) $\because$ 点$P$为直线$AB$上方抛物线上的任意一点,$\therefore$ 设点$P(x,- x^2 + 4x - 3)(0 < x < 3)$,则$D(x,x - 3)$,$\therefore PD = - x^2 + 4x - 3 - (x - 3) = - x^2 + 3x = - (x - 1.5)^2 + 2.25$,$\therefore$ 当$x = 1.5$时,$PD$有最大值,为$2.25$,此时$P(1.5,0.75)$.