1.「2025山西运城盐湖期中」关于y的一元二次方程$5y^{2}-20= 0$的解是(
A.$y= 2$
B.$y_{1}= 2,y_{2}= -2$
C.$y_{1}= y_{2}= 4$
D.$y_{1}= y_{2}= -2$
B
)A.$y= 2$
B.$y_{1}= 2,y_{2}= -2$
C.$y_{1}= y_{2}= 4$
D.$y_{1}= y_{2}= -2$
答案:B 移项得 $ 5y^{2}=20 $,系数化为1得 $ y^{2}=4 $,直接开平方得 $ y=\pm 2 $,$ \therefore y_{1}=2 $,$ y_{2}=-2 $。故选B。
2.「2025江苏宿迁宿豫月考」一元二次方程$x^{2}+m= 0(m<0)$的解是(
A.$x_{1}= -\sqrt {m},x_{2}= \sqrt {m}$
B.$x_{1}= \sqrt {m},x_{2}= \sqrt {-m}$
C.$x_{1}= -\sqrt {-m},x_{2}= \sqrt {-m}$
D.无解
C
)A.$x_{1}= -\sqrt {m},x_{2}= \sqrt {m}$
B.$x_{1}= \sqrt {m},x_{2}= \sqrt {-m}$
C.$x_{1}= -\sqrt {-m},x_{2}= \sqrt {-m}$
D.无解
答案:C $ x^{2}+m=0(m<0) $,移项得 $ x^{2}=-m $,直接开平方得 $ x=\pm \sqrt{-m} $,即 $ x_{1}=-\sqrt{-m} $,$ x_{2}=\sqrt{-m} $。故选C。
3.解下列方程:
(1)$3x^{2}-18= 0.$
解:原方程可化为 $ x^{2}=6 $,
$ \therefore x=\pm \sqrt{6} $,$ \therefore x_{1}=$
(2)$9x^{2}-5= 3.$
解:原方程可化为 $ x^{2}=$
$ \therefore x_{1}=$
(1)$3x^{2}-18= 0.$
解:原方程可化为 $ x^{2}=6 $,
$ \therefore x=\pm \sqrt{6} $,$ \therefore x_{1}=$
$\sqrt{6}$
,$ x_{2}=$$-\sqrt{6}$
。(2)$9x^{2}-5= 3.$
解:原方程可化为 $ x^{2}=$
$\frac{8}{9}$
,$ \therefore x=\pm $$\frac{2\sqrt{2}}{3}$
,$ \therefore x_{1}=$
$\frac{2\sqrt{2}}{3}$
,$ x_{2}=$$-\frac{2\sqrt{2}}{3}$
。答案:解析 (1) 原方程可化为 $ x^{2}=6 $,
$ \therefore x=\pm \sqrt{6} $,$ \therefore x_{1}=\sqrt{6} $,$ x_{2}=-\sqrt{6} $。
(2) 原方程可化为 $ x^{2}=\frac{8}{9} $,$ \therefore x=\pm \frac{2\sqrt{2}}{3} $,
$ \therefore x_{1}=\frac{2\sqrt{2}}{3} $,$ x_{2}=-\frac{2\sqrt{2}}{3} $。
$ \therefore x=\pm \sqrt{6} $,$ \therefore x_{1}=\sqrt{6} $,$ x_{2}=-\sqrt{6} $。
(2) 原方程可化为 $ x^{2}=\frac{8}{9} $,$ \therefore x=\pm \frac{2\sqrt{2}}{3} $,
$ \therefore x_{1}=\frac{2\sqrt{2}}{3} $,$ x_{2}=-\frac{2\sqrt{2}}{3} $。
4.「2025江苏南京期中」若关于x的方程$(x-4)^{2}= m+1$有实数根,则m的取值范围是(
A.$m≥0$
B.$m≥-1$
C.$m>-1$
D.$m>1$
B
)A.$m≥0$
B.$m≥-1$
C.$m>-1$
D.$m>1$
答案:B $ \because $ 关于 $ x $ 的方程 $ (x - 4)^{2}=m + 1 $ 有实数根,$ \therefore m + 1\geqslant 0 $,解得 $ m\geqslant - 1 $。故选B。
5.「2025重庆北碚期中」已知三角形的两边长分别为4和6,第三边的长是一元二次方程$(x-5)^{2}-9= 0$的一个根,则三角形的周长为____
18
.答案:答案 18
解析 $ \because (x - 5)^{2}-9 = 0 $,$ \therefore (x - 5)^{2}=9 $,$ \therefore x - 5=\pm 3 $,解得 $ x_{1}=2 $,$ x_{2}=8 $,当第三边长为2时,$ 2 + 4 = 6 $,不符合题意;当第三边长为8时,$ 4 + 6 = 10>8 $,符合题意,此时周长为 $ 8 + 6 + 4 = 18 $。
解析 $ \because (x - 5)^{2}-9 = 0 $,$ \therefore (x - 5)^{2}=9 $,$ \therefore x - 5=\pm 3 $,解得 $ x_{1}=2 $,$ x_{2}=8 $,当第三边长为2时,$ 2 + 4 = 6 $,不符合题意;当第三边长为8时,$ 4 + 6 = 10>8 $,符合题意,此时周长为 $ 8 + 6 + 4 = 18 $。
6.解方程:
(1)$(4x+1)^{2}-\frac {16}{9}= 0.$
解:$(4x + 1)^{2}=\frac{16}{9}$,两边直接开平方,得$4x + 1=\pm \frac{4}{3}$,解得$x_{1}=$
(2)$4(2x-1)^{2}-25(x+1)^{2}= 0.$
解:移项,得$4(2x - 1)^{2}=25(x + 1)^{2}$,整理,得$[2(2x - 1)]^{2}=[5(x + 1)]^{2}$,直接开平方,得$2(2x - 1)=\pm 5(x + 1)$,即$2(2x - 1)=5(x + 1)$或$2(2x - 1)=-5(x + 1)$,解得$x_{1}=$
(1)$(4x+1)^{2}-\frac {16}{9}= 0.$
解:$(4x + 1)^{2}=\frac{16}{9}$,两边直接开平方,得$4x + 1=\pm \frac{4}{3}$,解得$x_{1}=$
$\frac{1}{12}$
,$x_{2}=$$-\frac{7}{12}$
。(2)$4(2x-1)^{2}-25(x+1)^{2}= 0.$
解:移项,得$4(2x - 1)^{2}=25(x + 1)^{2}$,整理,得$[2(2x - 1)]^{2}=[5(x + 1)]^{2}$,直接开平方,得$2(2x - 1)=\pm 5(x + 1)$,即$2(2x - 1)=5(x + 1)$或$2(2x - 1)=-5(x + 1)$,解得$x_{1}=$
$-7$
,$x_{2}=$$-\frac{1}{3}$
。答案:解析 (1) $ \because (4x + 1)^{2}-\frac{16}{9}=0 $,$ \therefore (4x + 1)^{2}=\frac{16}{9} $,
两边直接开平方,得 $ 4x + 1=\pm \frac{4}{3} $,
解得 $ x_{1}=\frac{1}{12} $,$ x_{2}=-\frac{7}{12} $。
(2) 移项,得 $ 4(2x - 1)^{2}=25(x + 1)^{2} $,整理,得 $ [2(2x - 1)]^{2}=[5(x + 1)]^{2} $,直接开平方,得 $ 2(2x - 1)=\pm 5(x + 1) $,即 $ 2(2x - 1)=5(x + 1) $ 或 $ 2(2x - 1)=-5(x + 1) $,解得 $ x_{1}=-7 $,$ x_{2}=-\frac{1}{3} $。
两边直接开平方,得 $ 4x + 1=\pm \frac{4}{3} $,
解得 $ x_{1}=\frac{1}{12} $,$ x_{2}=-\frac{7}{12} $。
(2) 移项,得 $ 4(2x - 1)^{2}=25(x + 1)^{2} $,整理,得 $ [2(2x - 1)]^{2}=[5(x + 1)]^{2} $,直接开平方,得 $ 2(2x - 1)=\pm 5(x + 1) $,即 $ 2(2x - 1)=5(x + 1) $ 或 $ 2(2x - 1)=-5(x + 1) $,解得 $ x_{1}=-7 $,$ x_{2}=-\frac{1}{3} $。
7.「2024江苏南通崇川月考,★☆」下列方程不能用直接开平方法求解的是(
A.$x^{2}-4= 0$
B.$(x-1)^{2}-9= 0$
C.$x^{2}+3x= 0$
D.$(x-1)^{2}= (2x+1)^{2}$
C
)A.$x^{2}-4= 0$
B.$(x-1)^{2}-9= 0$
C.$x^{2}+3x= 0$
D.$(x-1)^{2}= (2x+1)^{2}$
答案:C A. $ x^{2}-4 = 0 $,移项得 $ x^{2}=4 $,直接开平方得 $ x_{1}=2 $,$ x_{2}=-2 $,故A不符合题意;B. $ (x - 1)^{2}-9 = 0 $,移项得 $ (x - 1)^{2}=9 $,直接开平方得 $ x - 1=\pm 3 $,即 $ x - 1 = 3 $ 或 $ x - 1=-3 $,$ \therefore x = 4 $ 或 $ x=-2 $,故B不符合题意;C. $ x^{2}+3x = 0 $,不适合用直接开平方法求解;D. $ (x - 1)^{2}=(2x + 1)^{2} $,直接开平方得 $ x - 1=\pm (2x + 1) $,即 $ x - 1 = 2x + 1 $ 或 $ x - 1=-(2x + 1) $,$ \therefore x=-2 $ 或 $ x = 0 $,故D不符合题意。故选C。
8.「2025河南南阳内乡期中,★☆」如图所示的是一个简单的程序计算器,若输出的数值为-10,则输入x的值为(
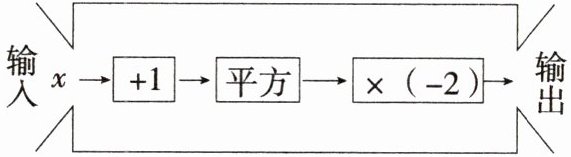
A.-8
B.$2\sqrt {5}-1或-2\sqrt {5}-1$
C.$\sqrt {5}-1或-\sqrt {5}-1$
D.$\sqrt {5}-1$
C
)
A.-8
B.$2\sqrt {5}-1或-2\sqrt {5}-1$
C.$\sqrt {5}-1或-\sqrt {5}-1$
D.$\sqrt {5}-1$
答案:C 根据题意,得 $ (x + 1)^{2}\times (-2)=-10 $,$ \therefore (x + 1)^{2}=5 $,$ \therefore x + 1=\pm \sqrt{5} $,$ \therefore x=-1\pm \sqrt{5} $。故选C。
9.「2023河南南阳南召月考,★☆」关于一元二次方程$2023(x-2)^{2}= 2024$的两个根判断正确的是(
A.一根小于1,另一根大于3
B.一根小于-2,另一根大于2
C.两根都小于0
D.两根都小于2
A
)A.一根小于1,另一根大于3
B.一根小于-2,另一根大于2
C.两根都小于0
D.两根都小于2
答案:A $ 2023(x - 2)^{2}=2024 $,整理,得 $ (x - 2)^{2}=\frac{2024}{2023} $,直接开平方,得 $ x - 2=\pm \sqrt{\frac{2024}{2023}} $,解得 $ x_{1}=2+\sqrt{\frac{2024}{2023}} $,$ x_{2}=2-\sqrt{\frac{2024}{2023}} $,$ \because \sqrt{\frac{2024}{2023}}>1 $,$ \therefore $ 方程的一根小于1,另一根大于3。故选A。
10.「2025江苏扬州仪征月考,★☆」若一元二次方程$ax^{2}= b(ab>0)的两个根分别是m+1与2m-4$,则$\frac {b}{a}= $
4
.答案:答案 4
解析 由 $ ax^{2}=b(ab>0) $ 得 $ x^{2}=\frac{b}{a} $,解得 $ x=\pm \sqrt{\frac{b}{a}} $,可知两根互为相反数。$ \because $ 一元二次方程 $ ax^{2}=b(ab>0) $ 的两个根分别是 $ m + 1 $ 与 $ 2m - 4 $,$ \therefore m + 1 + 2m - 4 = 0 $,解得 $ m = 1 $,$ \therefore $ 一元二次方程 $ ax^{2}=b(ab>0) $ 的两个根分别是2和-2,$ \therefore \sqrt{\frac{b}{a}}=2 $,$ \therefore \frac{b}{a}=4 $。
解析 由 $ ax^{2}=b(ab>0) $ 得 $ x^{2}=\frac{b}{a} $,解得 $ x=\pm \sqrt{\frac{b}{a}} $,可知两根互为相反数。$ \because $ 一元二次方程 $ ax^{2}=b(ab>0) $ 的两个根分别是 $ m + 1 $ 与 $ 2m - 4 $,$ \therefore m + 1 + 2m - 4 = 0 $,解得 $ m = 1 $,$ \therefore $ 一元二次方程 $ ax^{2}=b(ab>0) $ 的两个根分别是2和-2,$ \therefore \sqrt{\frac{b}{a}}=2 $,$ \therefore \frac{b}{a}=4 $。
11.「2025上海徐汇期中,★☆」已知$(a^{2}+b^{2}+3)\cdot (a^{2}+b^{2}-3)= 7$,则$a^{2}+b^{2}=$
4
.答案:答案 4
解析 设 $ t = a^{2}+b^{2}(t\geqslant 0) $,则原方程转化为 $ (t + 3)(t - 3)=7 $,整理,得 $ t^{2}-9 = 7 $。解得 $ t_{1}=4 $,$ t_{2}=-4 $(舍去)。即 $ a^{2}+b^{2}=4 $。
解析 设 $ t = a^{2}+b^{2}(t\geqslant 0) $,则原方程转化为 $ (t + 3)(t - 3)=7 $,整理,得 $ t^{2}-9 = 7 $。解得 $ t_{1}=4 $,$ t_{2}=-4 $(舍去)。即 $ a^{2}+b^{2}=4 $。