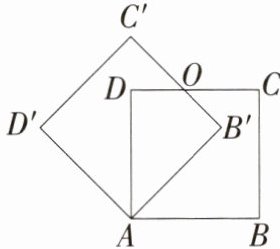
8.「2025陕西延安富县期中,」如图,把边长为1的正方形ABCD绕点A逆时针旋转45°得到正方形AB'C'D',边B'C'与DC交于点O,则四边形AB'OD的面积为( )
A.2
B.2√2
C.√2 - 1
D.2 - √2

A.2
B.2√2
C.√2 - 1
D.2 - √2
答案:
C 如图,连接$AC$,$\because$正方形$ABCD$绕点$A$逆时针旋转$45^{\circ}$后得到正方形$AB'C'D'$,
$\therefore A$、$B'$、$C$三点共线,$AB'=AB=1$,$\angle AB'C'=\angle B=90^{\circ}$,$\because$四边形$ABCD$为正方形,
$\therefore \angle BAC=\angle ACD=45^{\circ}$,$AC=\sqrt{2}AB=\sqrt{2}$,
$\therefore \triangle OCB'$为等腰直角三角形,
$\because CB'=AC-AB'=\sqrt{2}-1$,$\therefore OB'=CB'=\sqrt{2}-1$,
$\therefore$四边形$AB'OD$的面积$=S_{\triangle ADC}-S_{\triangle OCB'}=\frac{1}{2}\times 1\times 1-\frac{1}{2}\times (\sqrt{2}-1)\times (\sqrt{2}-1)=\sqrt{2}-1$.故选C.
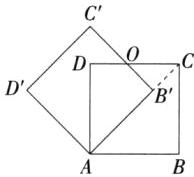
C 如图,连接$AC$,$\because$正方形$ABCD$绕点$A$逆时针旋转$45^{\circ}$后得到正方形$AB'C'D'$,
$\therefore A$、$B'$、$C$三点共线,$AB'=AB=1$,$\angle AB'C'=\angle B=90^{\circ}$,$\because$四边形$ABCD$为正方形,
$\therefore \angle BAC=\angle ACD=45^{\circ}$,$AC=\sqrt{2}AB=\sqrt{2}$,
$\therefore \triangle OCB'$为等腰直角三角形,
$\because CB'=AC-AB'=\sqrt{2}-1$,$\therefore OB'=CB'=\sqrt{2}-1$,
$\therefore$四边形$AB'OD$的面积$=S_{\triangle ADC}-S_{\triangle OCB'}=\frac{1}{2}\times 1\times 1-\frac{1}{2}\times (\sqrt{2}-1)\times (\sqrt{2}-1)=\sqrt{2}-1$.故选C.

9.「2025辽宁抚顺新抚月考,」如图,在Rt△ABC中,∠ACB= 90°,∠A= 30°,BC= 1,将△ABC绕点C顺时针旋转得到△A'B'C,其中点A'与点A是对应点,点B'与点B是对应点,若点B'恰好落在AB边上,则点A到直线A'C的距离等于( )

A.1
B.√3
C.3/2
D.3√3/2

A.1
B.√3
C.3/2
D.3√3/2
答案:
C 如图,过点$A$作$AH\perp A'C$于$H$,$\because \angle ACB=90^{\circ}$,$\angle CAB=30^{\circ}$,$BC=1$,$\therefore \angle B=60^{\circ}$,$AB=2$,
在$Rt\triangle ABC$中,由勾股定理得$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{3}$,$\because$将$\triangle ABC$绕点$C$顺时针旋转得到$\triangle A'B'C$,
$\therefore CB=CB'$,$\angle A'CB'=\angle ACB=90^{\circ}$,
$\therefore \angle B=\angle CB'B=60^{\circ}$,$\therefore \angle BCB'=60^{\circ}$,
易证$\angle ACH=\angle BCB'=60^{\circ}$,
$\because \angle AHC=90^{\circ}$,$\therefore \angle CAH=30^{\circ}$,$\therefore CH=\frac{1}{2}AC=\frac{\sqrt{3}}{2}$,
在$Rt\triangle ACH$中,由勾股定理得$AH=\sqrt{AC^{2}-CH^{2}}=\frac{3}{2}$,$\therefore$点$A$到直线$A'C$的距离等于$\frac{3}{2}$.故选C.

C 如图,过点$A$作$AH\perp A'C$于$H$,$\because \angle ACB=90^{\circ}$,$\angle CAB=30^{\circ}$,$BC=1$,$\therefore \angle B=60^{\circ}$,$AB=2$,
在$Rt\triangle ABC$中,由勾股定理得$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{3}$,$\because$将$\triangle ABC$绕点$C$顺时针旋转得到$\triangle A'B'C$,
$\therefore CB=CB'$,$\angle A'CB'=\angle ACB=90^{\circ}$,
$\therefore \angle B=\angle CB'B=60^{\circ}$,$\therefore \angle BCB'=60^{\circ}$,
易证$\angle ACH=\angle BCB'=60^{\circ}$,
$\because \angle AHC=90^{\circ}$,$\therefore \angle CAH=30^{\circ}$,$\therefore CH=\frac{1}{2}AC=\frac{\sqrt{3}}{2}$,
在$Rt\triangle ACH$中,由勾股定理得$AH=\sqrt{AC^{2}-CH^{2}}=\frac{3}{2}$,$\therefore$点$A$到直线$A'C$的距离等于$\frac{3}{2}$.故选C.

10.学科对角互补模型「2025广东广州海珠期中,」如图,点F为正方形ABCD对角线AC的中点,将以点F为直角顶点的直角△FEG绕点F旋转(△FEG的边EG始终在正方形ABCD外),若正方形ABCD的边长为3,则在旋转过程中,△FEG与正方形ABCD重叠部分的面积为( )

A.9
B.3
C.4.5
D.2.25

A.9
B.3
C.4.5
D.2.25
答案:
D 如图,连接$FD$,$\because$点$F$是$AC$的中点,四边形$ABCD$是正方形,
$\therefore \angle DFC=90^{\circ}$,$DF=FC$,$\angle FDN=\angle FCM=45^{\circ}$,$\therefore \angle DFN+\angle NFC=90^{\circ}$,
$\because EF\perp FG$,$\therefore \angle MFC+\angle NFC=90^{\circ}$,$\therefore \angle DFN=\angle CFM$,$\therefore \triangle MFC\cong \triangle NFD(ASA)$,$\therefore S_{\triangle MFC}=S_{\triangle NFD}$,
$\therefore S_{四边形FMCN}=S_{\triangle MFC}+S_{\triangle NFC}=S_{\triangle NFD}+S_{\triangle NFC}=S_{\triangle DFC}$,
$\because$正方形$ABCD$的边长为$3$,$\therefore AC=3\sqrt{2}$,$\therefore FD=FC=\frac{3\sqrt{2}}{2}$,
$\therefore S_{\triangle DFC}=\frac{1}{2}FD\cdot FC=\frac{1}{2}\times \frac{3\sqrt{2}}{2}\times \frac{3\sqrt{2}}{2}=2.25$,$\therefore$重叠部分的面积为$2.25$.故选D.

D 如图,连接$FD$,$\because$点$F$是$AC$的中点,四边形$ABCD$是正方形,
$\therefore \angle DFC=90^{\circ}$,$DF=FC$,$\angle FDN=\angle FCM=45^{\circ}$,$\therefore \angle DFN+\angle NFC=90^{\circ}$,
$\because EF\perp FG$,$\therefore \angle MFC+\angle NFC=90^{\circ}$,$\therefore \angle DFN=\angle CFM$,$\therefore \triangle MFC\cong \triangle NFD(ASA)$,$\therefore S_{\triangle MFC}=S_{\triangle NFD}$,
$\therefore S_{四边形FMCN}=S_{\triangle MFC}+S_{\triangle NFC}=S_{\triangle NFD}+S_{\triangle NFC}=S_{\triangle DFC}$,
$\because$正方形$ABCD$的边长为$3$,$\therefore AC=3\sqrt{2}$,$\therefore FD=FC=\frac{3\sqrt{2}}{2}$,
$\therefore S_{\triangle DFC}=\frac{1}{2}FD\cdot FC=\frac{1}{2}\times \frac{3\sqrt{2}}{2}\times \frac{3\sqrt{2}}{2}=2.25$,$\therefore$重叠部分的面积为$2.25$.故选D.

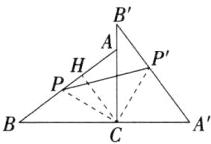
11.「2025天津南开中学月考,」如图,在△ABC中,∠ACB= 90°,BC= 2,∠BAC=
30°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM,则PM的最大值是______.

30°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM,则PM的最大值是______.

答案:
答案 $3$
解析 如图,连接$PC$.在$Rt\triangle ABC$中,$\because \angle A=30^{\circ}$,$BC=2$,$\therefore AB=4$,根据旋转的性质可知,$A'B'=AB=4$,$\because P$为$A'B'$的中点,$\triangle A'B'C$为直角三角形,$\therefore PC=\frac{1}{2}A'B'=2$,
$\because M$是$BC$的中点,$\therefore CM=\frac{1}{2}BC=1$,$\because PM\leqslant PC+CM=3$,
$\therefore$当$P$、$C$、$M$共线,且$C$在$P$、$M$之间时,$PM$取得最大值,最大值为$3$.

答案 $3$
解析 如图,连接$PC$.在$Rt\triangle ABC$中,$\because \angle A=30^{\circ}$,$BC=2$,$\therefore AB=4$,根据旋转的性质可知,$A'B'=AB=4$,$\because P$为$A'B'$的中点,$\triangle A'B'C$为直角三角形,$\therefore PC=\frac{1}{2}A'B'=2$,
$\because M$是$BC$的中点,$\therefore CM=\frac{1}{2}BC=1$,$\because PM\leqslant PC+CM=3$,
$\therefore$当$P$、$C$、$M$共线,且$C$在$P$、$M$之间时,$PM$取得最大值,最大值为$3$.

12.「2025河南驻马店一中期末,」如图,在△ABC中,∠ACB= 90°,AC= 3,BC= 4,将△ABC绕点C顺时针旋转90°得到△A'B'C,若P为边AB上一动点,旋转后点P的对应点为点P',则线段PP'长度的取值范围是______.


答案:
答案 $\frac{12\sqrt{2}}{5}\leqslant PP'\leqslant 4\sqrt{2}$
解析 如图,连接$PC$,$P'C$,过点$C$作$CH\perp AB$于$H$,$\because$将$\triangle ABC$绕点$C$顺时针旋转$90^{\circ}$得到$\triangle A'B'C$,
$\therefore PC=P'C$,$\angle PCP'=90^{\circ}$,$\therefore PP'=\sqrt{2}CP$.
$\because \angle ACB=90^{\circ}$,$AC=3$,$BC=4$,
$\therefore AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{9 + 16}=5$,
$\because S_{\triangle ABC}=\frac{1}{2}\times 3\times 4=\frac{1}{2}\times 5CH$,$\therefore CH=\frac{12}{5}$,
$\because P$为边$AB$上一动点,$\therefore$当点$P$与点$B$重合时,$CP$有最大值,为$4$,此时$PP'$的值最大,为$4\sqrt{2}$,当点$P$与点$H$重合时,$CP$有最小值,为$\frac{12}{5}$,此时$PP'$的值最小,为$\frac{12\sqrt{2}}{5}$,
$\therefore$线段$PP'$长度的取值范围为$\frac{12\sqrt{2}}{5}\leqslant PP'\leqslant 4\sqrt{2}$.
答案 $\frac{12\sqrt{2}}{5}\leqslant PP'\leqslant 4\sqrt{2}$
解析 如图,连接$PC$,$P'C$,过点$C$作$CH\perp AB$于$H$,$\because$将$\triangle ABC$绕点$C$顺时针旋转$90^{\circ}$得到$\triangle A'B'C$,
$\therefore PC=P'C$,$\angle PCP'=90^{\circ}$,$\therefore PP'=\sqrt{2}CP$.
$\because \angle ACB=90^{\circ}$,$AC=3$,$BC=4$,
$\therefore AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{9 + 16}=5$,
$\because S_{\triangle ABC}=\frac{1}{2}\times 3\times 4=\frac{1}{2}\times 5CH$,$\therefore CH=\frac{12}{5}$,
$\because P$为边$AB$上一动点,$\therefore$当点$P$与点$B$重合时,$CP$有最大值,为$4$,此时$PP'$的值最大,为$4\sqrt{2}$,当点$P$与点$H$重合时,$CP$有最小值,为$\frac{12}{5}$,此时$PP'$的值最小,为$\frac{12\sqrt{2}}{5}$,
$\therefore$线段$PP'$长度的取值范围为$\frac{12\sqrt{2}}{5}\leqslant PP'\leqslant 4\sqrt{2}$.

13.学科分类讨论思想「2025河南安阳期中,」如图,在△ABC中,∠C= ∠ABC= 30°,△ADE是直角三角形,∠ADE= 90°,∠E= 30°,且边AB与AD重合,将△ADE绕点A以每秒5°的速度沿顺时针方向旋转一周,在旋转的过程中,第______秒时,边DE所在直线与边AC所在直线平行.


答案:
答案 $6$或$42$
解析 分两种情况:①当$DE$在$AB$上方时,如图1所示,$\because DE// AC$,$\therefore \angle D+\angle DAC=180^{\circ}$,
$\because \angle D=90^{\circ}$,$\therefore \angle DAC=90^{\circ}$.
$\because \angle C=\angle ABC=30^{\circ}$,$\therefore \angle BAC=120^{\circ}$,
$\therefore \angle BAD=120^{\circ}-90^{\circ}=30^{\circ}$,
$\therefore$在旋转的过程中,第$30^{\circ}\div 5^{\circ}=6$(秒)时,边$DE$所在直线与边$AC$所在直线平行.
②当$DE$在$AB$下方时,如图2所示,
$\because DE// AC$,$\therefore \angle CAD=\angle D=90^{\circ}$,
$\because \angle C=\angle ABC=30^{\circ}$,$\therefore \angle BAC=120^{\circ}$,
$\therefore \triangle ADE$旋转的度数为$120^{\circ}+90^{\circ}=210^{\circ}$,
$\therefore$在旋转的过程中,第$210^{\circ}\div 5^{\circ}=42$(秒)时,边$DE$所在直线与边$AC$所在直线平行.
综上所述,第$6$或$42$秒时,边$DE$所在直线与边$AC$所在直线平行.


答案 $6$或$42$
解析 分两种情况:①当$DE$在$AB$上方时,如图1所示,$\because DE// AC$,$\therefore \angle D+\angle DAC=180^{\circ}$,
$\because \angle D=90^{\circ}$,$\therefore \angle DAC=90^{\circ}$.
$\because \angle C=\angle ABC=30^{\circ}$,$\therefore \angle BAC=120^{\circ}$,
$\therefore \angle BAD=120^{\circ}-90^{\circ}=30^{\circ}$,
$\therefore$在旋转的过程中,第$30^{\circ}\div 5^{\circ}=6$(秒)时,边$DE$所在直线与边$AC$所在直线平行.
②当$DE$在$AB$下方时,如图2所示,
$\because DE// AC$,$\therefore \angle CAD=\angle D=90^{\circ}$,
$\because \angle C=\angle ABC=30^{\circ}$,$\therefore \angle BAC=120^{\circ}$,
$\therefore \triangle ADE$旋转的度数为$120^{\circ}+90^{\circ}=210^{\circ}$,
$\therefore$在旋转的过程中,第$210^{\circ}\div 5^{\circ}=42$(秒)时,边$DE$所在直线与边$AC$所在直线平行.
综上所述,第$6$或$42$秒时,边$DE$所在直线与边$AC$所在直线平行.


14.新课标推理能力「2025北京工业大学实验学校期中」如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①OM+ON的值不变;②∠PNM= ∠POB;③MN的长不变;④四边形PMON的面积不变.其中正确的结论是(

A.①②③
B.①②④
C.①③④
D.②③④
B
)
A.①②③
B.①②④
C.①③④
D.②③④
答案:B 如图,过$P$作$PE\perp OA$于$E$,$PF\perp OB$于$F$,$\therefore \angle PEO=\angle PFO=90^{\circ}$,$\because OP$为$\angle AOB$的平分线,$\therefore \angle EOP=\angle FOP$,
又$\because OP=OP$,$\therefore \triangle POE\cong \triangle POF(AAS)$,$\therefore OE=OF$,$PE=PF$.
$\because \angle EPF+\angle AOB=360^{\circ}-90^{\circ}-90^{\circ}=180^{\circ}$,$\angle MPN+\angle AOB=180^{\circ}$,$\therefore \angle EPF=\angle MPN$,$\therefore \angle EPM=\angle FPN$;$\because \angle PEM=\angle PFN=90^{\circ}$,$\therefore \triangle PEM\cong \triangle PFN(ASA)$,
$\therefore EM=NF$,$PM=PN$,$\therefore OM+ON=OE+OF=$定值,故①正确.
$\because \triangle PEM\cong \triangle PFN$,$\therefore S_{\triangle PEM}=S_{\triangle PNF}$,$\therefore S_{四边形PMON}=S_{四边形PEOF}=$定值,故④正确.
设$\angle MPN=x^{\circ}$,$\because PM=PN$,$\therefore \angle PNM=\angle PMN=\frac{1}{2}\times (180^{\circ}-x^{\circ})=90^{\circ}-\frac{1}{2}x^{\circ}$,
$\because \angle AOB+\angle MPN=180^{\circ}$,$\therefore \angle AOB=180^{\circ}-x^{\circ}$,$\therefore \angle POB=\frac{1}{2}\times (180^{\circ}-x^{\circ})=90^{\circ}-\frac{1}{2}x^{\circ}$,$\therefore \angle PNM=\angle POB$,故②正确.
在旋转过程中,$\triangle PMN$都是等腰三角形,且$\angle MPN$不变,$\because PM$的长度是变化的,$\therefore MN$的长度也是变化的,故③错误.
综上所述,正确的结论是①②④,故选B.
又$\because OP=OP$,$\therefore \triangle POE\cong \triangle POF(AAS)$,$\therefore OE=OF$,$PE=PF$.
$\because \angle EPF+\angle AOB=360^{\circ}-90^{\circ}-90^{\circ}=180^{\circ}$,$\angle MPN+\angle AOB=180^{\circ}$,$\therefore \angle EPF=\angle MPN$,$\therefore \angle EPM=\angle FPN$;$\because \angle PEM=\angle PFN=90^{\circ}$,$\therefore \triangle PEM\cong \triangle PFN(ASA)$,
$\therefore EM=NF$,$PM=PN$,$\therefore OM+ON=OE+OF=$定值,故①正确.
$\because \triangle PEM\cong \triangle PFN$,$\therefore S_{\triangle PEM}=S_{\triangle PNF}$,$\therefore S_{四边形PMON}=S_{四边形PEOF}=$定值,故④正确.
设$\angle MPN=x^{\circ}$,$\because PM=PN$,$\therefore \angle PNM=\angle PMN=\frac{1}{2}\times (180^{\circ}-x^{\circ})=90^{\circ}-\frac{1}{2}x^{\circ}$,
$\because \angle AOB+\angle MPN=180^{\circ}$,$\therefore \angle AOB=180^{\circ}-x^{\circ}$,$\therefore \angle POB=\frac{1}{2}\times (180^{\circ}-x^{\circ})=90^{\circ}-\frac{1}{2}x^{\circ}$,$\therefore \angle PNM=\angle POB$,故②正确.
在旋转过程中,$\triangle PMN$都是等腰三角形,且$\angle MPN$不变,$\because PM$的长度是变化的,$\therefore MN$的长度也是变化的,故③错误.
综上所述,正确的结论是①②④,故选B.