1.新考向尺规作图如图,$\triangle ABC$中,$AB = AC > BC$,将$\triangle ABC绕点C顺时针旋转得到\triangle DEC$,使得点$B的对应点E落在边AB$上(点$E不与点B$重合)。
(1)尺规作图:作出$\triangle DEC$。
(2)试判断线段$AB$、$CD$的位置关系。

(1)尺规作图:作出$\triangle DEC$。
(2)试判断线段$AB$、$CD$的位置关系。

答案:
解析 (1) 如图,$\triangle DEC$ 即为所求。

(2) $CD // AB$。
理由:由旋转的性质得 $\angle DEC = \angle B$,$DC = AC$,$DE = AB$,$\because AB = AC$,$\therefore DE = DC$,$\therefore \angle DEC = \angle DCE$,$\because CB = CE$,$\therefore \angle B = \angle CEB$,$\therefore \angle DCE = \angle CEB$,$\therefore CD // AB$。
解析 (1) 如图,$\triangle DEC$ 即为所求。

(2) $CD // AB$。
理由:由旋转的性质得 $\angle DEC = \angle B$,$DC = AC$,$DE = AB$,$\because AB = AC$,$\therefore DE = DC$,$\therefore \angle DEC = \angle DCE$,$\because CB = CE$,$\therefore \angle B = \angle CEB$,$\therefore \angle DCE = \angle CEB$,$\therefore CD // AB$。
2.「2025吉林四平期末」如图,$\triangle ABC三个顶点的坐标分别为A(2,4)$,$B(1,1)$,$C(4,3)$。
(1)$\triangle ABC$的面积是____。
(2)请画出$\triangle ABC绕点B顺时针旋转90^{\circ}后的\triangle A_{1}BC_{1}$。
(3)已知点$P(0,m)为y$轴上一点,当$PA + PB$取得最小值时,$m$的值是____。

(1)$\triangle ABC$的面积是____。
(2)请画出$\triangle ABC绕点B顺时针旋转90^{\circ}后的\triangle A_{1}BC_{1}$。
(3)已知点$P(0,m)为y$轴上一点,当$PA + PB$取得最小值时,$m$的值是____。

答案:
解析 (1) $\frac{7}{2}$。
(2) 如图,$\triangle A_1BC_1$ 即为所求。

(3) 2。
提示:如图,作点 $A$ 关于 $y$ 轴的对称点 $A'$,连接 $A'B$,当 $P$ 为 $A'B$ 与 $y$ 轴的交点时,$PA + PB$ 取得最小值。$\because A(2,4)$,$\therefore A'(-2,4)$,设直线 $A'B$ 的解析式为 $y = kx + b$,将点 $A'(-2,4)$,$B(1,1)$ 代入,得 $\begin{cases}-2k + b = 4, \\ k + b = 1,\end{cases}$ 解得 $\begin{cases}k = -1, \\ b = 2,\end{cases}$ $\therefore$ 直线 $A'B$ 的解析式为 $y = -x + 2$,令 $x = 0$,得 $y = 2$,$\therefore$ 点 $P$ 的坐标为 $(0,2)$,$\therefore m = 2$。
解析 (1) $\frac{7}{2}$。
(2) 如图,$\triangle A_1BC_1$ 即为所求。

(3) 2。
提示:如图,作点 $A$ 关于 $y$ 轴的对称点 $A'$,连接 $A'B$,当 $P$ 为 $A'B$ 与 $y$ 轴的交点时,$PA + PB$ 取得最小值。$\because A(2,4)$,$\therefore A'(-2,4)$,设直线 $A'B$ 的解析式为 $y = kx + b$,将点 $A'(-2,4)$,$B(1,1)$ 代入,得 $\begin{cases}-2k + b = 4, \\ k + b = 1,\end{cases}$ 解得 $\begin{cases}k = -1, \\ b = 2,\end{cases}$ $\therefore$ 直线 $A'B$ 的解析式为 $y = -x + 2$,令 $x = 0$,得 $y = 2$,$\therefore$ 点 $P$ 的坐标为 $(0,2)$,$\therefore m = 2$。
3.学科教材变式特色P76T2利用如图所示的图案,通过下列变换设计图案,使所设计的图案中包含4个这样的基本图案。
(1)通过平移设计图案。
(2)通过旋转设计图案。

(1)通过平移设计图案。
(2)通过旋转设计图案。

答案:
解析 (1) 答案不唯一,如图所示。

(2) 答案不唯一,如图所示。

解析 (1) 答案不唯一,如图所示。

(2) 答案不唯一,如图所示。

4.「2023浙江温州中考,★☆☆」如图,在$2×4的方格纸ABCD$中,每个小方格的边长为1。已知格点$P$,请按要求画格点三角形(顶点均在格点上)。
(1)在图1中画一个等腰三角形$PEF$,使底边长为$\sqrt{2}$,点$E在BC$上,点$F在AD$上,再画出该三角形绕矩形$ABCD的中心旋转180^{\circ}$后的图形。
(2)在图2中画一个$Rt\triangle PQR$,使$∠P = 45^{\circ}$,点$Q在BC$上,点$R在AD$上,再画出该三角形向右平移1个单位后的图形。

(1)在图1中画一个等腰三角形$PEF$,使底边长为$\sqrt{2}$,点$E在BC$上,点$F在AD$上,再画出该三角形绕矩形$ABCD的中心旋转180^{\circ}$后的图形。
(2)在图2中画一个$Rt\triangle PQR$,使$∠P = 45^{\circ}$,点$Q在BC$上,点$R在AD$上,再画出该三角形向右平移1个单位后的图形。

答案:
解析 (1) 如图①或图②。


(2) 如图③或图④。


解析 (1) 如图①或图②。


(2) 如图③或图④。


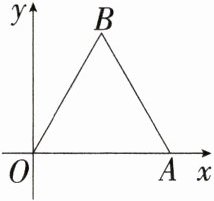
5.新课标运算能力如图,等边三角形$OAB$在平面直角坐标系中,已知点$A(2,0)$,将$\triangle OAB绕点O沿顺时针方向旋转\alpha^{\circ}(0 < \alpha < 360)得\triangle OA_{1}B_{1}$。
(1)求点$B$的坐标。
(2)当点$A_{1}与点B_{1}$的纵坐标相同时,求$\alpha的值及点B_{1}$的坐标。
(1)求点$B$的坐标。
(2)当点$A_{1}与点B_{1}$的纵坐标相同时,求$\alpha的值及点B_{1}$的坐标。

答案:
解析 (1) 过点 $B$ 作 $BC \perp OA$,垂足为 $C$(图略),$\because A(2,0)$,$\therefore OA = 2$。$\because \triangle OAB$ 为等边三角形,$BC \perp OA$,$\therefore OC = CA = 1$,$OB = OA = 2$。由勾股定理得 $BC = \sqrt{3}$。$\therefore$ 点 $B$ 的坐标为 $(1,\sqrt{3})$。
(2) $\because$ 点 $B_1$ 与点 $A_1$ 的纵坐标相同,$\therefore A_1B_1 // OA$。
如图①,当 $\alpha = 300$ 时,点 $A_1$ 与点 $B_1$ 的纵坐标相同,由旋转的性质可知 $A_1B_1 = AB = OA = 2$。$\because$ 点 $B$ 的坐标为 $(1,\sqrt{3})$,$\therefore$ 易得点 $B_1$ 的坐标为 $(-1,\sqrt{3})$。


如图②,当 $\alpha = 120$ 时,点 $A$ 与点 $B$ 的纵坐标相同,设 $A_1B_1$ 与 $y$ 轴交于点 $E$,易得 $\angle B_1OE = 30^{\circ}$,$\angle B_1EO = 90^{\circ}$,$OB = 2$,$\therefore B_1E = \frac{1}{2}OB = 1$,$\therefore OE = \sqrt{2^2 - 1^2} = \sqrt{3}$,$\therefore$ 点 $B_1$ 的坐标为 $(1,-\sqrt{3})$。
综上,当 $\alpha = 300$ 或 $120$ 时,$A_1$ 与 $B_1$ 的纵坐标相同,对应的点 $B_1$ 的坐标为 $(-1,\sqrt{3})$ 或 $(1,-\sqrt{3})$。
解析 (1) 过点 $B$ 作 $BC \perp OA$,垂足为 $C$(图略),$\because A(2,0)$,$\therefore OA = 2$。$\because \triangle OAB$ 为等边三角形,$BC \perp OA$,$\therefore OC = CA = 1$,$OB = OA = 2$。由勾股定理得 $BC = \sqrt{3}$。$\therefore$ 点 $B$ 的坐标为 $(1,\sqrt{3})$。
(2) $\because$ 点 $B_1$ 与点 $A_1$ 的纵坐标相同,$\therefore A_1B_1 // OA$。
如图①,当 $\alpha = 300$ 时,点 $A_1$ 与点 $B_1$ 的纵坐标相同,由旋转的性质可知 $A_1B_1 = AB = OA = 2$。$\because$ 点 $B$ 的坐标为 $(1,\sqrt{3})$,$\therefore$ 易得点 $B_1$ 的坐标为 $(-1,\sqrt{3})$。


如图②,当 $\alpha = 120$ 时,点 $A$ 与点 $B$ 的纵坐标相同,设 $A_1B_1$ 与 $y$ 轴交于点 $E$,易得 $\angle B_1OE = 30^{\circ}$,$\angle B_1EO = 90^{\circ}$,$OB = 2$,$\therefore B_1E = \frac{1}{2}OB = 1$,$\therefore OE = \sqrt{2^2 - 1^2} = \sqrt{3}$,$\therefore$ 点 $B_1$ 的坐标为 $(1,-\sqrt{3})$。
综上,当 $\alpha = 300$ 或 $120$ 时,$A_1$ 与 $B_1$ 的纵坐标相同,对应的点 $B_1$ 的坐标为 $(-1,\sqrt{3})$ 或 $(1,-\sqrt{3})$。