1.「2025浙江杭州萧山月考」如图,$△ABC$是等边三角形,$AB= 4$,$AD是边BC$上的高,点$E在边AD$上,连接$BE$,以$BE为边在其下方作等边△BEF$,连接$DF$、$CF$,则$DF$的最小值为____。


答案:
答案 1
解析 ∵△ABC和△BEF都是等边三角形,∴∠ABC=∠EBF=60°,AB=BC,BE=BF,∴∠ABE=∠CBF=60°−∠EBC,∴△ABE≌△CBF(SAS),如图,取AB的中点M,连接EM,由△ABE≌△CBF易得DF=EM,∴当ME⊥AD时,ME有最小值,即DF有最小值。∵△ABC是等边三角形,AB =4,AD是边BC上的高,∴∠BAD=30°,AM=2,当ME⊥AD
时,在Rt△AME中,∠MAE=30°,∴ME=$\frac{1}{2}$AM=1。∴DF的最小值为1。

答案 1
解析 ∵△ABC和△BEF都是等边三角形,∴∠ABC=∠EBF=60°,AB=BC,BE=BF,∴∠ABE=∠CBF=60°−∠EBC,∴△ABE≌△CBF(SAS),如图,取AB的中点M,连接EM,由△ABE≌△CBF易得DF=EM,∴当ME⊥AD时,ME有最小值,即DF有最小值。∵△ABC是等边三角形,AB =4,AD是边BC上的高,∴∠BAD=30°,AM=2,当ME⊥AD
时,在Rt△AME中,∠MAE=30°,∴ME=$\frac{1}{2}$AM=1。∴DF的最小值为1。

2.如图,在$Rt△ABC$中,$∠ACB= 90°$,$AC= 4$,$BC= 3$,$AB= 5$,点$E是线段AB$上的动点,连接$CE$,并将线段$CE绕点C逆时针旋转90°至CD$,连接$BD$,则$BD$的最小值为____。


答案:
答案 $\frac{3}{5}$
解析 如图,在AC上截取CF=CB=3,连接EF,BF,由旋转的性质可得CE=CD,∠ECD=90°,∴∠DCB=∠ECF=90°−∠BCE,∴△ECF≌△DCB(SAS),∴EF=DB,由垂线段最短可知,当FE⊥AB时,EF有最小值,即BD有最小值,此时,$S_{△ABC}=\frac{1}{2}×3×4=\frac{1}{2}×3×3+\frac{1}{2}×5×EF$,∴EF=$\frac{3}{5}$,∴BD的最小值为$\frac{3}{5}$。

答案 $\frac{3}{5}$
解析 如图,在AC上截取CF=CB=3,连接EF,BF,由旋转的性质可得CE=CD,∠ECD=90°,∴∠DCB=∠ECF=90°−∠BCE,∴△ECF≌△DCB(SAS),∴EF=DB,由垂线段最短可知,当FE⊥AB时,EF有最小值,即BD有最小值,此时,$S_{△ABC}=\frac{1}{2}×3×4=\frac{1}{2}×3×3+\frac{1}{2}×5×EF$,∴EF=$\frac{3}{5}$,∴BD的最小值为$\frac{3}{5}$。

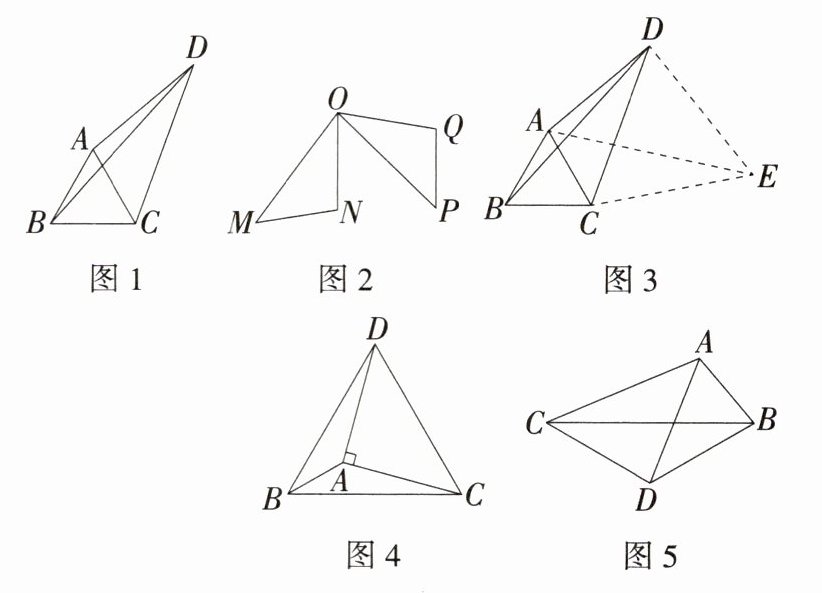
3.新考向实践探究题【问题背景】学校数学兴趣小组在专题学习中遇到一个几何问题:如图1,已知等边$△ABC$,$D是△ABC$外一点,连接$AD$、$CD$、$BD$,若$∠ADC= 30°$,$AD= 3$,$BD= 5$,求$CD$的长。该小组在研究图2中$△OMN≌△OPQ$时得到启示,于是作出图3,从而获得了以下的解题思路,请你帮忙完善解题过程。
解:如图3所示,以$DC为边作等边△CDE$,连接$AE$。
∵$△ABC和△DCE$都是等边三角形,
∴$BC= AC$,$DC= EC$,$∠BCA= ∠DCE= 60°$。
∴$∠BCA+∠ACD= $____$+∠ACD$,
∴$∠BCD= ∠ACE$,
∴____,∴$AE= BD= 5$。
∵$∠ADC= 30°$,$∠CDE= 60°$,
∴$∠ADE= ∠ADC+∠CDE= 90°$。
∵$AD= 3$,∴$Rt△ADE$中,$DE= \sqrt{AE^{2}-AD^{2}}= 4$,
∴$CD= DE= $____。
【尝试应用】如图4,在$△ABC$中,$∠ABC= 45°$,$AB= \sqrt{2}$,$BC= 4$,以$AC$为直角边,$A为直角顶点作等腰直角△ACD$,连接$BD$,求$BD$的长。
【拓展创新】如图5,在$△ABC$中,$AB= 4$,$AC= 8$,以$BC为边向外作等腰△BCD$,$BD= CD$,$∠BDC= 120°$,连接$AD$,求$AD$的最大值。
解:如图3所示,以$DC为边作等边△CDE$,连接$AE$。
∵$△ABC和△DCE$都是等边三角形,
∴$BC= AC$,$DC= EC$,$∠BCA= ∠DCE= 60°$。
∴$∠BCA+∠ACD= $____$+∠ACD$,
∴$∠BCD= ∠ACE$,
∴____,∴$AE= BD= 5$。
∵$∠ADC= 30°$,$∠CDE= 60°$,
∴$∠ADE= ∠ADC+∠CDE= 90°$。
∵$AD= 3$,∴$Rt△ADE$中,$DE= \sqrt{AE^{2}-AD^{2}}= 4$,
∴$CD= DE= $____。
【尝试应用】如图4,在$△ABC$中,$∠ABC= 45°$,$AB= \sqrt{2}$,$BC= 4$,以$AC$为直角边,$A为直角顶点作等腰直角△ACD$,连接$BD$,求$BD$的长。
【拓展创新】如图5,在$△ABC$中,$AB= 4$,$AC= 8$,以$BC为边向外作等腰△BCD$,$BD= CD$,$∠BDC= 120°$,连接$AD$,求$AD$的最大值。

答案:
解析 [问题背景]∠DCE;△BCD≌△ACE;4。
[尝试应用]如图,以点A为旋转中心,将△ABD绕点A顺时针旋转90°,得到△AEC,连接BE,由旋转的性质可得AB=AE,∠BAE=∠DAC=90°,∴∠EBA=45°,∵∠ABC=45°,∴∠EBC=∠EBA+∠ABC=90°,在Rt△ABE中,∵AB=AE=$\sqrt{2}$,∴BE=$\sqrt{AB^{2}+AE^{2}}$=2,在Rt△BEC中,∵BC=4,∴EC=$\sqrt{EB^{2}+BC^{2}}$=2$\sqrt{5}$,∴由旋转的性质可得BD=EC=2$\sqrt{5}$。
[拓展创新]如图,以点D为旋转中心,将△ACD绕点D顺时针旋转120°,得到△BDF,连接AF,由旋转的性质可得AD=DF,∠ADF=120°,AC=BF,∴∠DAF=∠DFA=30°,过点D作DE⊥AF,∴DE=$\frac{1}{2}$AD,AE=$\frac{1}{2}$AF,在Rt△ADE中,AD=$\sqrt{DE^{2}+AE^{2}}=\sqrt{(\frac{1}{2}AD)^{2}+(\frac{1}{2}AF)^{2}}$,化简得AD=$\frac{\sqrt{3}}{3}$AF,∴当AF取得最大值时,AD取得最大值,当A、B、F三点共线时,AF最大,∵AB=4,AC=8,∴AF的最大值为AB+BF=AB+AC=12,∴AD的最大值为$\frac{\sqrt{3}}{3}$×12=4$\sqrt{3}$。

解析 [问题背景]∠DCE;△BCD≌△ACE;4。
[尝试应用]如图,以点A为旋转中心,将△ABD绕点A顺时针旋转90°,得到△AEC,连接BE,由旋转的性质可得AB=AE,∠BAE=∠DAC=90°,∴∠EBA=45°,∵∠ABC=45°,∴∠EBC=∠EBA+∠ABC=90°,在Rt△ABE中,∵AB=AE=$\sqrt{2}$,∴BE=$\sqrt{AB^{2}+AE^{2}}$=2,在Rt△BEC中,∵BC=4,∴EC=$\sqrt{EB^{2}+BC^{2}}$=2$\sqrt{5}$,∴由旋转的性质可得BD=EC=2$\sqrt{5}$。
[拓展创新]如图,以点D为旋转中心,将△ACD绕点D顺时针旋转120°,得到△BDF,连接AF,由旋转的性质可得AD=DF,∠ADF=120°,AC=BF,∴∠DAF=∠DFA=30°,过点D作DE⊥AF,∴DE=$\frac{1}{2}$AD,AE=$\frac{1}{2}$AF,在Rt△ADE中,AD=$\sqrt{DE^{2}+AE^{2}}=\sqrt{(\frac{1}{2}AD)^{2}+(\frac{1}{2}AF)^{2}}$,化简得AD=$\frac{\sqrt{3}}{3}$AF,∴当AF取得最大值时,AD取得最大值,当A、B、F三点共线时,AF最大,∵AB=4,AC=8,∴AF的最大值为AB+BF=AB+AC=12,∴AD的最大值为$\frac{\sqrt{3}}{3}$×12=4$\sqrt{3}$。
