1.「2024山东淄博月考」如图,在$\odot O$中,$AB$为直径,$CD\perp AB于C$,四边形$CDEF$是正方形,连接$BD$,若$CO= 3$,$OF= 1$,则$BD= $( )

A.$3\sqrt{5}$
B.$4\sqrt{5}$
C.13
D.$2\sqrt{10}$

A.$3\sqrt{5}$
B.$4\sqrt{5}$
C.13
D.$2\sqrt{10}$
答案:
B 如图,连接DO,∵CO=3,OF=1,∴CF=4,∵四边形CDEF是正方形,∴∠DCO=90°,CD=CF=4,∴OD= $\sqrt{CD^{2}+CO^{2}}=\sqrt{4^{2}+3^{2}}=5$,∴OB=OD=5,∴CB=CO+OB=8,∴BD=$\sqrt{CD^{2}+CB^{2}}=\sqrt{4^{2}+8^{2}}=4\sqrt{5}$。故选B。

B 如图,连接DO,∵CO=3,OF=1,∴CF=4,∵四边形CDEF是正方形,∴∠DCO=90°,CD=CF=4,∴OD= $\sqrt{CD^{2}+CO^{2}}=\sqrt{4^{2}+3^{2}}=5$,∴OB=OD=5,∴CB=CO+OB=8,∴BD=$\sqrt{CD^{2}+CB^{2}}=\sqrt{4^{2}+8^{2}}=4\sqrt{5}$。故选B。

2.如图,点$D$、$E分别在\triangle ABC的边BC$、$AB$上,过$A$、$C$、$D三点的圆的圆心为点E$,过$B$、$F$、$E三点的圆的圆心为D$,如果$\angle A= 57^{\circ}$,那么$\angle ABC= $______$^{\circ}$.


答案:
答案 22
解析 如图,连接EC、ED,设∠ABC=x,

∵EA=EC,∴∠A=∠ACE=57°,∴∠4=180°−2∠A=180°−2×57°=66°,∵DB=DE,∴∠1=∠ABC=x,∴∠2=∠1+∠ABC=2x,∵EC=ED,∴∠3=∠2=2x,∵∠4=∠3+∠ABC,∴2x+x=66°,解得x=22°,即∠ABC=22°。故答案为22。
答案 22
解析 如图,连接EC、ED,设∠ABC=x,

∵EA=EC,∴∠A=∠ACE=57°,∴∠4=180°−2∠A=180°−2×57°=66°,∵DB=DE,∴∠1=∠ABC=x,∴∠2=∠1+∠ABC=2x,∵EC=ED,∴∠3=∠2=2x,∵∠4=∠3+∠ABC,∴2x+x=66°,解得x=22°,即∠ABC=22°。故答案为22。
3.「2025浙江绍兴期中」如图,$\odot O$的半径为10,弦$AB= 16$,点$M是弦AB上的动点且点M不与点A$、$B$重合,若$OM$的长为整数,则这样的点$M$有( )

A.4个
B.5个
C.7个
D.9个

A.4个
B.5个
C.7个
D.9个
答案:
C 如图,过点O作OP⊥AB于点P,连接OA,∵AB=16,∴AP=$\frac{1}{2}AB=8$,∵OA=10,∴OP=$\sqrt{OA^{2}-AP^{2}}=6$,∵点M是弦AB上的动点且点M不与点A、B重合,∴6≤OM<10,∵OM的长为整数,∴OM可取6,7,8,9,∴满足条件的点M有7个。故选C。

C 如图,过点O作OP⊥AB于点P,连接OA,∵AB=16,∴AP=$\frac{1}{2}AB=8$,∵OA=10,∴OP=$\sqrt{OA^{2}-AP^{2}}=6$,∵点M是弦AB上的动点且点M不与点A、B重合,∴6≤OM<10,∵OM的长为整数,∴OM可取6,7,8,9,∴满足条件的点M有7个。故选C。

4.新中华优秀传统文化「2025安徽阜阳太和期中」如图,筒车是我国古代发明的一种水利灌溉工具,明代科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,筒车盛水桶的运行轨道是以轴心$O$为圆心的圆,已知圆心$O$在水面上方,且$\odot O被水面截得的弦AB$的长为16米,$\odot O$的半径长为10米.若点$C$为运行轨道的最低点,则点$C到弦AB$所在直线的距离是( )

A.4米
B.6米
C.8米
D.10米

A.4米
B.6米
C.8米
D.10米
答案:
A 如图,连接OA、OC,OC交AB于点D,由题意得OA=OC=10米,OC⊥AB,
∴AD=BD=$\frac{1}{2}AB=8$米,∠ADO=90°,
∴OD=$\sqrt{OA^{2}-AD^{2}}=\sqrt{10^{2}-8^{2}}=6$(米),
∴CD=OC-OD=4米,
即点C到弦AB所在直线的距离是4米。故选A。

A 如图,连接OA、OC,OC交AB于点D,由题意得OA=OC=10米,OC⊥AB,
∴AD=BD=$\frac{1}{2}AB=8$米,∠ADO=90°,
∴OD=$\sqrt{OA^{2}-AD^{2}}=\sqrt{10^{2}-8^{2}}=6$(米),
∴CD=OC-OD=4米,
即点C到弦AB所在直线的距离是4米。故选A。

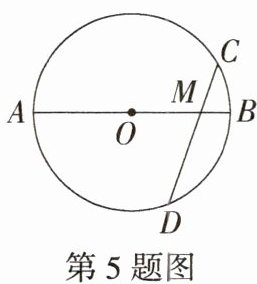
5.「2024江苏扬州高邮期末」如图,$\odot O的直径AB和弦CD相交于点M$,已知$AM= 5$,$BM= 1$,$\angle CMB= 60^{\circ}$,则$CD$的长为______.

答案:
答案 $2\sqrt{6}$
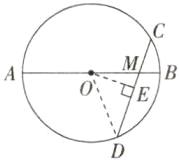
解析 如图,连接OD,过点O作OE⊥CD于点E,则CD=2DE。
∵∠CMB=60°,∴∠OME=∠CMB=60°,∵OE⊥CD,∴∠OEM=90°,∴∠MOE=90°−60°=30°,∵AM=5,BM=1,∴OD=OB=$\frac{1}{2}(AM+BM)=3$,∴OM=3−1=2,∴EM=1,∴OE=$\sqrt{OM^{2}-ME^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$,∴DE=$\sqrt{OD^{2}-OE^{2}}=\sqrt{3^{2}-(\sqrt{3})^{2}}=\sqrt{6}$,∴CD=2$\sqrt{6}$。
方法总结:在解决有关弦的问题时,常将半径、圆心到弦的垂线段、弦的一半构建在一个直角三角形中,再利用勾股定理解浃问题。
答案 $2\sqrt{6}$
解析 如图,连接OD,过点O作OE⊥CD于点E,则CD=2DE。
∵∠CMB=60°,∴∠OME=∠CMB=60°,∵OE⊥CD,∴∠OEM=90°,∴∠MOE=90°−60°=30°,∵AM=5,BM=1,∴OD=OB=$\frac{1}{2}(AM+BM)=3$,∴OM=3−1=2,∴EM=1,∴OE=$\sqrt{OM^{2}-ME^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$,∴DE=$\sqrt{OD^{2}-OE^{2}}=\sqrt{3^{2}-(\sqrt{3})^{2}}=\sqrt{6}$,∴CD=2$\sqrt{6}$。
方法总结:在解决有关弦的问题时,常将半径、圆心到弦的垂线段、弦的一半构建在一个直角三角形中,再利用勾股定理解浃问题。

6.「2024陕西西安模拟」如图,点$A$、$B$、$C$、$D$、$E都在\odot O$上,$BE$是直径,$BE// CD$,$\angle E= 28^{\circ}$,则$\angle A$的度数为( )

A.$28^{\circ}$
B.$56^{\circ}$
C.$62^{\circ}$
D.$68^{\circ}$

A.$28^{\circ}$
B.$56^{\circ}$
C.$62^{\circ}$
D.$68^{\circ}$
答案:
C 如图,连接BC,∵BE//CD,∠E=28°,∴∠ECD=∠E=28°,∵BE是⊙O的直径,∴∠BCE=90°,∴∠BCD=90°+28°=118°,∵四边形ABCD为⊙O的内接四边形,∴∠A+∠BCD=180°,∴∠A=180°−∠BCD=62°。故选C。

C 如图,连接BC,∵BE//CD,∠E=28°,∴∠ECD=∠E=28°,∵BE是⊙O的直径,∴∠BCE=90°,∴∠BCD=90°+28°=118°,∵四边形ABCD为⊙O的内接四边形,∴∠A+∠BCD=180°,∴∠A=180°−∠BCD=62°。故选C。

7.「2023浙江杭州萧山模拟」如图,$A$、$B$、$C$、$D四个点均在\odot O$上,$\angle AOD= \alpha$,$AO// DC$,$\angle B= \beta$,则$\alpha$,$\beta$满足的关系为( )

A.$2\alpha-\beta=90^{\circ}$
B.$\alpha+\beta=90^{\circ}$
C.$2\beta+\alpha=180^{\circ}$
D.$\alpha+9\beta=540^{\circ}$

A.$2\alpha-\beta=90^{\circ}$
B.$\alpha+\beta=90^{\circ}$
C.$2\beta+\alpha=180^{\circ}$
D.$\alpha+9\beta=540^{\circ}$
答案:
C 如图,连接AD,∵AO//DC,∴∠ODC=∠AOD=α。∵OD=OA,∴∠ODA=∠OAD=$\frac{1}{2}(180°-∠AOD)=\frac{1}{2}(180°-α)$。∵四边形ABCD是⊙O的内接四边形,∴∠B+∠ADC=180°,即β+$\frac{1}{2}(180°-α)+α=180°$,整理得2β+α=180°。故选C。

C 如图,连接AD,∵AO//DC,∴∠ODC=∠AOD=α。∵OD=OA,∴∠ODA=∠OAD=$\frac{1}{2}(180°-∠AOD)=\frac{1}{2}(180°-α)$。∵四边形ABCD是⊙O的内接四边形,∴∠B+∠ADC=180°,即β+$\frac{1}{2}(180°-α)+α=180°$,整理得2β+α=180°。故选C。

8.「2025湖北十堰期中」如图,已知六边形$ABCDEF内接于\odot O$,$\angle CAE= 60^{\circ}$,则$\angle B+\angle F$的度数是( )

A.$230^{\circ}$
B.$240^{\circ}$
C.$235^{\circ}$
D.$245^{\circ}$

A.$230^{\circ}$
B.$240^{\circ}$
C.$235^{\circ}$
D.$245^{\circ}$
答案:
B 如图,连接CF,
∵∠CAE和∠CFE都是$\overset{\frown}{CE}$所对的圆周角,
∴∠CFE=∠CAE=60°。
∵四边形ABCF是⊙O的内接四边形,
∴∠B+∠AFC=180°,
∴∠B+∠AFE=∠B+∠AFC+∠CFE=180°+60°=240°。故选B。

B 如图,连接CF,
∵∠CAE和∠CFE都是$\overset{\frown}{CE}$所对的圆周角,
∴∠CFE=∠CAE=60°。
∵四边形ABCF是⊙O的内接四边形,
∴∠B+∠AFC=180°,
∴∠B+∠AFE=∠B+∠AFC+∠CFE=180°+60°=240°。故选B。

9.「2025山西大同期中」如图,$AB是\odot O$的直径,点$C$,$D$,$E在\odot O$上,若$\angle AED= 18^{\circ}$,则$\angle BCD$的度数为( )

A.$70^{\circ}$
B.$36^{\circ}$
C.$54^{\circ}$
D.$72^{\circ}$

A.$70^{\circ}$
B.$36^{\circ}$
C.$54^{\circ}$
D.$72^{\circ}$
答案:
D 如图,连接AC,∵∠AED=18°,
∴∠ACD=∠AED=18°,∵AB是⊙O的直径,∴∠ACB=90°,∴∠BCD=∠ACB-∠ACD=90°-18°=72°。故选D。

D 如图,连接AC,∵∠AED=18°,
∴∠ACD=∠AED=18°,∵AB是⊙O的直径,∴∠ACB=90°,∴∠BCD=∠ACB-∠ACD=90°-18°=72°。故选D。
