10.「2025北京大兴一模」如图,$AB是\odot O$的弦,且$AB= 6$,点$C是弧AB$的中点,点$D是优弧AB$上的一点,$\angle ADC= 30^{\circ}$,则圆心$O到弦AB$的距离为______.


答案:
答案 $\sqrt{3}$
解析 如图,连接OA、OC,OC交AB于点E,∵点C是弧AB的中点,AB=6,∴OC⊥AB,且AE=BE=3,∵∠ADC=30°,∴∠AOC=2∠ADC=60°,∴∠OAE=30°,∴OA=2OE,又∵OE²+AE²=OA²,∴OE²+3²=4OE²,∴OE=$\sqrt{3}$,即圆心O到弦AB的距离为$\sqrt{3}$。

答案 $\sqrt{3}$
解析 如图,连接OA、OC,OC交AB于点E,∵点C是弧AB的中点,AB=6,∴OC⊥AB,且AE=BE=3,∵∠ADC=30°,∴∠AOC=2∠ADC=60°,∴∠OAE=30°,∴OA=2OE,又∵OE²+AE²=OA²,∴OE²+3²=4OE²,∴OE=$\sqrt{3}$,即圆心O到弦AB的距离为$\sqrt{3}$。

11.「2025湖北宜昌西陵期中」如图,点$A$、$B$、$P在\odot O$上,$\angle APB= 50^{\circ}$,若$M是\odot O$上的动点,则等腰$\triangle ABM$顶角的度数为
50°或80°或130°
.答案:答案 50°或80°或130°
解析 连接AM,BM(图略),
①若点M在优弧APB上,则∠M=∠APB=50°。
若AM=BM,则等腰△ABM顶角的度数为50°;
若AM=AB或BM=AB,则等腰△ABM顶角的度数为180°−2∠M=80°。
②若点M在劣弧AB上,易得∠M=180°−∠APB=130°,此时∠M是顶角。
∴等腰△ABM顶角的度数为50°或80°或130°。
解析 连接AM,BM(图略),
①若点M在优弧APB上,则∠M=∠APB=50°。
若AM=BM,则等腰△ABM顶角的度数为50°;
若AM=AB或BM=AB,则等腰△ABM顶角的度数为180°−2∠M=80°。
②若点M在劣弧AB上,易得∠M=180°−∠APB=130°,此时∠M是顶角。
∴等腰△ABM顶角的度数为50°或80°或130°。
12.「2024天津西青期末」如图,$AB为\odot O$的直径,弦$CD和AB$相交,若$\angle ABC= 38^{\circ}$,则$\angle D$的大小是( )

A.$38^{\circ}$
B.$52^{\circ}$
C.$60^{\circ}$
D.$70^{\circ}$

A.$38^{\circ}$
B.$52^{\circ}$
C.$60^{\circ}$
D.$70^{\circ}$
答案:
B 如图,连接AC,∵AB为⊙O的直径,∴∠ACB=90°,∵∠ABC=38°,∴∠A=90°-∠ABC=52°,∴∠D=∠A=52°。故选B。

B 如图,连接AC,∵AB为⊙O的直径,∴∠ACB=90°,∵∠ABC=38°,∴∠A=90°-∠ABC=52°,∴∠D=∠A=52°。故选B。

13.「2024湖北随州广水期中」如图,$AB是\odot O$的直径,$\angle ACD= \angle CAB$,$AD= 3$,$AC= 6$,则$\odot O$的半径为______.


答案:
答案 $\frac{3\sqrt{5}}{2}$
解析 如图,连接BC,∵AB是直径,∴∠ACB=90°。∵∠ACD=∠CAB,∴$\overset{\frown}{AD}=\overset{\frown}{BC}$,∴BC=AD=3,在Rt△ABC中,AB=$\sqrt{AC^{2}+BC^{2}}=\sqrt{6^{2}+3^{2}}=3\sqrt{5}$,∴⊙O的半径为$\frac{3\sqrt{5}}{2}$。

答案 $\frac{3\sqrt{5}}{2}$
解析 如图,连接BC,∵AB是直径,∴∠ACB=90°。∵∠ACD=∠CAB,∴$\overset{\frown}{AD}=\overset{\frown}{BC}$,∴BC=AD=3,在Rt△ABC中,AB=$\sqrt{AC^{2}+BC^{2}}=\sqrt{6^{2}+3^{2}}=3\sqrt{5}$,∴⊙O的半径为$\frac{3\sqrt{5}}{2}$。

14.「2025浙江嘉兴秀洲期中」如图,$AB是\odot O$的一条弦,将劣弧沿弦$AB$翻折,连接$AO$并延长,交翻折后的弧于点$C$,连接$BC$.若$\odot O$的半径为2,$BC= 1$,则$AB= $______.


答案:
答案 $\sqrt{15}$
解析 如图,延长AC交⊙O于点D,连接BD,
∵劣弧沿弦AB翻折,AD交翻折后的弧于点C,且$\overset{\frown}{BC}$和$\overset{\frown}{BD}$所对的圆周角都是∠BAD,
∴$\overset{\frown}{BC}=\overset{\frown}{BD}$,∴BC=BD=1,
∵AD为⊙O的直径,⊙O的半径为2,
∴∠ABD=90°,AD=4,
∴AB=$\sqrt{AD^{2}-BD^{2}}=\sqrt{4^{2}-1^{2}}=\sqrt{15}$。

答案 $\sqrt{15}$
解析 如图,延长AC交⊙O于点D,连接BD,
∵劣弧沿弦AB翻折,AD交翻折后的弧于点C,且$\overset{\frown}{BC}$和$\overset{\frown}{BD}$所对的圆周角都是∠BAD,
∴$\overset{\frown}{BC}=\overset{\frown}{BD}$,∴BC=BD=1,
∵AD为⊙O的直径,⊙O的半径为2,
∴∠ABD=90°,AD=4,
∴AB=$\sqrt{AD^{2}-BD^{2}}=\sqrt{4^{2}-1^{2}}=\sqrt{15}$。

15.如图,$\odot O$的半径为4,将三角尺的$60^{\circ}$、$90^{\circ}角的顶点A$,$B$放在圆上,$AC$,$BC两边分别与\odot O交于D$,$E$两点,连接$DE$,且$BE= DE$,则$\triangle ABC$的面积为______.


答案:
答案 $24\sqrt{3}$
解析 如图,连接AE,∵∠CBA=90°,
∴AE为⊙O的直径,∵⊙O的半径为4,∴AE=8。∵BE=DE,∴∠BAE=∠DAE,∵∠BAC=60°,∴∠BAE=∠DAE=30°,∴BE=DE=$\frac{1}{2}AE=4$,
∴AB=$\sqrt{AE^{2}-BE^{2}}=\sqrt{8^{2}-4^{2}}=4\sqrt{3}$;∵AE为直径,∴∠EDA=90°,∴∠EDC=180°−90°=90°,∵∠C=30°,∴CE=2DE=8,∴BC=BE+CE=12,∴S△ABC=$\frac{1}{2}AB·BC=\frac{1}{2}×4\sqrt{3}×12=24\sqrt{3}$。

答案 $24\sqrt{3}$
解析 如图,连接AE,∵∠CBA=90°,
∴AE为⊙O的直径,∵⊙O的半径为4,∴AE=8。∵BE=DE,∴∠BAE=∠DAE,∵∠BAC=60°,∴∠BAE=∠DAE=30°,∴BE=DE=$\frac{1}{2}AE=4$,
∴AB=$\sqrt{AE^{2}-BE^{2}}=\sqrt{8^{2}-4^{2}}=4\sqrt{3}$;∵AE为直径,∴∠EDA=90°,∴∠EDC=180°−90°=90°,∵∠C=30°,∴CE=2DE=8,∴BC=BE+CE=12,∴S△ABC=$\frac{1}{2}AB·BC=\frac{1}{2}×4\sqrt{3}×12=24\sqrt{3}$。

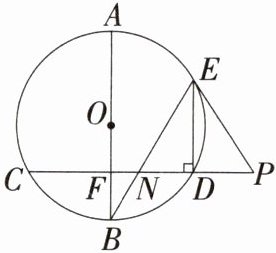
16.如图,$AB为\odot O$的直径,$E是弧AD$上一点,弦$DE// AB$,且$DE\perp弦CD$,连接$BE交CD于点N$,点$P在CD$的延长线上,$PN= PE$.若$OF= 6$,$BF= 4$,求$PN$的长.

答案:
解析 如图,连接CE,∵DE⊥CD,∴∠CDE=90°,∴CE为⊙O的直径,∴CE经过点O。
∵PN=PE,∴∠PEN=∠PNE,
∵OB=OE,∴∠OEB=∠OBE,由DE//AB,DE⊥CD 可得AB⊥CD,∴∠OBE+∠BNF=90°,∴∠OEB+∠PEN=90°,即∠PEC=90°,
∵AB⊥CD,∴CF=DF,
∵OC=OE,∴OF为△CED的中位线,∴DE=2OF=12,由OF=6,BF=4得OC=OB=10,∴CE=20,
∴CD=$\sqrt{CE^{2}-DE^{2}}=16$,设PD=x,则PC=x+16。
在Rt△PDE和Rt△PCE中,由勾股定理,得PD²+DE²=PE²=PC²-CE²,即x²+12²=(x+16)²-20²,解得x=9,∴PD=9。
∴PE=$\sqrt{PD^{2}+DE^{2}}=15$,∴PN=PE=15。
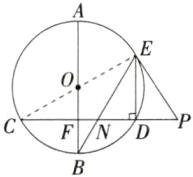
解析 如图,连接CE,∵DE⊥CD,∴∠CDE=90°,∴CE为⊙O的直径,∴CE经过点O。
∵PN=PE,∴∠PEN=∠PNE,
∵OB=OE,∴∠OEB=∠OBE,由DE//AB,DE⊥CD 可得AB⊥CD,∴∠OBE+∠BNF=90°,∴∠OEB+∠PEN=90°,即∠PEC=90°,
∵AB⊥CD,∴CF=DF,
∵OC=OE,∴OF为△CED的中位线,∴DE=2OF=12,由OF=6,BF=4得OC=OB=10,∴CE=20,
∴CD=$\sqrt{CE^{2}-DE^{2}}=16$,设PD=x,则PC=x+16。
在Rt△PDE和Rt△PCE中,由勾股定理,得PD²+DE²=PE²=PC²-CE²,即x²+12²=(x+16)²-20²,解得x=9,∴PD=9。
∴PE=$\sqrt{PD^{2}+DE^{2}}=15$,∴PN=PE=15。
