1.「2024天津滨海新区期中」已知$\odot O$的半径是4 cm,点A、B、C与圆心O的距离分别为4 cm、3 cm、5 cm,则点A在
圆上
,点B在圆内
,点C在圆外
.答案:答案 圆上;圆内;圆外
解析 ∵⊙O的半径是4cm,点A、B、C与圆心O的距离分别为4cm、3cm、5cm,∴点A在圆上,点B在圆内,点C在圆外
解析 ∵⊙O的半径是4cm,点A、B、C与圆心O的距离分别为4cm、3cm、5cm,∴点A在圆上,点B在圆内,点C在圆外
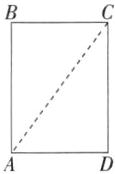
2.「2024上海杨浦期末」如图,矩形ABCD中,AB= 8,AD= 6,以A为圆心,r为半径作$\odot A$,使得点D在圆内,点C在圆外,则半径r的取值范围是____.


答案:
答案 6<r<10
解析 如图,连接AC,在矩形ABCD中,AB = CD = 8,AD = 6,∴AC = 10。∵以A为圆心,r为半径作⊙A,使得点D在圆内,点C在圆外,∴半径r的取值范围是6<r<10。
答案 6<r<10
解析 如图,连接AC,在矩形ABCD中,AB = CD = 8,AD = 6,∴AC = 10。∵以A为圆心,r为半径作⊙A,使得点D在圆内,点C在圆外,∴半径r的取值范围是6<r<10。

3.「2025山东滨州期末」在同一平面内,过已知A、B、C三个点可以作圆的个数为(
A.0
B.1
C.2
D.0或1
D
)A.0
B.1
C.2
D.0或1
答案:D 当A、B、C三个点共线时,过A、B、C三个点不能作圆;当A、B、C三个点不在同一条直线上时,过A、B、C三个点的圆有且只有一个。故选D。
4.「2025江苏镇江丹阳期中」如图,在平面直角坐标系中,A(1,6)、B(5,6)、C(7,4).
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为____.
(2)这个圆的半径为____.
(3)点D(5,-3)在$\odot M$____.(填“内”“外”或“上”)

(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为____.
(2)这个圆的半径为____.
(3)点D(5,-3)在$\odot M$____.(填“内”“外”或“上”)

答案:
解析 (1)(3,2)。
提示:作线段AB、BC的垂直平分线,垂直平分线的交点即为点M。

(2) $2\sqrt{5}$。
提示:∵M(3,2),∴MA = $\sqrt{(1 - 3)^2 + (6 - 2)^2} = 2\sqrt{5}$。即该圆的半径为 $2\sqrt{5}$。
(3) 外。
提示:∵D(5,-3),M(3,2),∴MD = $\sqrt{(5 - 3)^2 + (-3 - 2)^2} = \sqrt{29} > 2\sqrt{5}$,∴点D(5,-3)在⊙M 外。
解析 (1)(3,2)。
提示:作线段AB、BC的垂直平分线,垂直平分线的交点即为点M。

(2) $2\sqrt{5}$。
提示:∵M(3,2),∴MA = $\sqrt{(1 - 3)^2 + (6 - 2)^2} = 2\sqrt{5}$。即该圆的半径为 $2\sqrt{5}$。
(3) 外。
提示:∵D(5,-3),M(3,2),∴MD = $\sqrt{(5 - 3)^2 + (-3 - 2)^2} = \sqrt{29} > 2\sqrt{5}$,∴点D(5,-3)在⊙M 外。
5.下列关于三角形外心的说法中,错误的是(
A.三角形的外心到三个顶点的距离相等
B.三角形的外心是三条边的垂直平分线的交点
C.等腰三角形的外心在三角形内部
D.任何一个三角形有且只有一个外接圆
C
)A.三角形的外心到三个顶点的距离相等
B.三角形的外心是三条边的垂直平分线的交点
C.等腰三角形的外心在三角形内部
D.任何一个三角形有且只有一个外接圆
答案:C 当等腰三角形是钝角三角形时,外心在三角形外部,故C选项错误,故选C。
6.「2024吉林长春宽城期末」如图,$\triangle ABC内接于\odot O$.若$\odot O$的半径为3,$\angle C= 45^{\circ}$,则弦AB的长为____.


答案:
答案 $3\sqrt{2}$
解析 如图,连接OA,OB,∵∠ACB = 45°,∴∠AOB = 2∠ACB = 90°,∵OA = OB = 3,∴AB = $\sqrt{OA^2 + OB^2} = 3\sqrt{2}$。

答案 $3\sqrt{2}$
解析 如图,连接OA,OB,∵∠ACB = 45°,∴∠AOB = 2∠ACB = 90°,∵OA = OB = 3,∴AB = $\sqrt{OA^2 + OB^2} = 3\sqrt{2}$。

7.用反证法证明时,假设“点在圆内或圆外”,经过推理得出矛盾,则点和圆的位置关系是(
A.点在圆内
B.点在圆上
C.点在圆外
D.不确定
B
)A.点在圆内
B.点在圆上
C.点在圆外
D.不确定
答案:B 假设“点在圆内或圆外”,经过推理得出矛盾,即假设不成立,则点在圆上。故选B。
8.「2024山东烟台龙口一模,★☆」如图,在正方形方格中,A,B,C,D,E,P均在格点处,则点P是下列哪个三角形的外心( )

A.$\triangle ACE$
B.$\triangle ABD$
C.$\triangle ACD$
D.$\triangle BCE$

A.$\triangle ACE$
B.$\triangle ABD$
C.$\triangle ACD$
D.$\triangle BCE$
答案:
D 如图,设每个小正方形的边长均为1,由勾股定理得PC = PE = PB = $\sqrt{3^2 + 1^2} = \sqrt{10}$,∴P到B、C、E的距离相等,∴P是△BCE的外心。故选D。

D 如图,设每个小正方形的边长均为1,由勾股定理得PC = PE = PB = $\sqrt{3^2 + 1^2} = \sqrt{10}$,∴P到B、C、E的距离相等,∴P是△BCE的外心。故选D。

9.「2025浙江杭州期中,★☆」如图,在$Rt\triangle ABC$中,$\angle C= 90^{\circ}$,$\angle A= 30^{\circ}$,AB= 10,点O为AB的中点,以点C为圆心,5为半径作$\odot C$,则下列判断错误的是( )

A.点O在$\odot C$上
B.点B在$\odot C$上
C.点A在$\odot C$外
D.OB的中点在$\odot C$外

A.点O在$\odot C$上
B.点B在$\odot C$上
C.点A在$\odot C$外
D.OB的中点在$\odot C$外
答案:
D 如图,连接OC,取OB的中点D,连接CD,∵∠ACB = 90°,∠A = 30°,AB = 10,∴BC = $\frac{1}{2}AB = 5$,由勾股定理得AC = $\sqrt{AB^2 - BC^2} = 5\sqrt{3}$,∵点O为AB的中点,∴OC = $\frac{1}{2}AB = OA = OB = 5$,∴OC = BC = 5,∵以点C为圆心,5为半径作⊙C,∴点O和点B在⊙C上,故A、B选项判断正确,不符合题意;∵AC = $5\sqrt{3} > 5$,∴点A在⊙C外,故C选项判断正确,不符合题意;∵OC = OB = BC = 5,∴△BOC是等边三角形,∵D是OB的中点,∴CD⊥OB,∴在Rt△BCD中,CD < BC,即CD < 5,∴OB的中点在⊙C内,故D选项判断错误,符合题意。故选D。

D 如图,连接OC,取OB的中点D,连接CD,∵∠ACB = 90°,∠A = 30°,AB = 10,∴BC = $\frac{1}{2}AB = 5$,由勾股定理得AC = $\sqrt{AB^2 - BC^2} = 5\sqrt{3}$,∵点O为AB的中点,∴OC = $\frac{1}{2}AB = OA = OB = 5$,∴OC = BC = 5,∵以点C为圆心,5为半径作⊙C,∴点O和点B在⊙C上,故A、B选项判断正确,不符合题意;∵AC = $5\sqrt{3} > 5$,∴点A在⊙C外,故C选项判断正确,不符合题意;∵OC = OB = BC = 5,∴△BOC是等边三角形,∵D是OB的中点,∴CD⊥OB,∴在Rt△BCD中,CD < BC,即CD < 5,∴OB的中点在⊙C内,故D选项判断错误,符合题意。故选D。
