1.如图,点B在$\odot A$上,点C在$\odot A$外,以下条件不能判定BC是$\odot A$的切线的是(
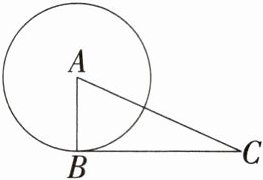
A.$∠A= 50^{\circ },∠C= 40^{\circ }$
B.$∠B-∠C= ∠A$
C.$AB^{2}+BC^{2}= AC^{2}$
D.$\odot A$与AC的交点是AC的中点
D
)
A.$∠A= 50^{\circ },∠C= 40^{\circ }$
B.$∠B-∠C= ∠A$
C.$AB^{2}+BC^{2}= AC^{2}$
D.$\odot A$与AC的交点是AC的中点
答案:D
A. $\because ∠A=50^{\circ },∠C=40^{\circ },\therefore ∠B=180^{\circ }-∠A-∠C=90^{\circ },\therefore BC⊥AB$,∵点B在$\odot A$上,$\therefore AB$是$\odot A$的半径,$\therefore BC$是$\odot A$的切线;
B. $\because ∠B-∠C=∠A,\therefore ∠B=∠A+∠C,\because ∠A+∠B+∠C=180^{\circ },\therefore ∠B=90^{\circ },\therefore BC⊥AB$,∵点B在$\odot A$上,$\therefore AB$是$\odot A$的半径,$\therefore BC$是$\odot A$的切线;
C. $\because AB^{2}+BC^{2}=AC^{2},\therefore △ABC$是直角三角形,$∠B=90^{\circ },\therefore BC⊥AB$,∵点B在$\odot A$上,$\therefore AB$是$\odot A$的半径,$\therefore BC$是$\odot A$的切线;
D. $\because \odot A$与AC的交点是AC的中点,$\therefore AB=\frac {1}{2}AC$,但不能证出$∠B=90^{\circ },\therefore $不能判定BC是$\odot A$的切线.故选D.
A. $\because ∠A=50^{\circ },∠C=40^{\circ },\therefore ∠B=180^{\circ }-∠A-∠C=90^{\circ },\therefore BC⊥AB$,∵点B在$\odot A$上,$\therefore AB$是$\odot A$的半径,$\therefore BC$是$\odot A$的切线;
B. $\because ∠B-∠C=∠A,\therefore ∠B=∠A+∠C,\because ∠A+∠B+∠C=180^{\circ },\therefore ∠B=90^{\circ },\therefore BC⊥AB$,∵点B在$\odot A$上,$\therefore AB$是$\odot A$的半径,$\therefore BC$是$\odot A$的切线;
C. $\because AB^{2}+BC^{2}=AC^{2},\therefore △ABC$是直角三角形,$∠B=90^{\circ },\therefore BC⊥AB$,∵点B在$\odot A$上,$\therefore AB$是$\odot A$的半径,$\therefore BC$是$\odot A$的切线;
D. $\because \odot A$与AC的交点是AC的中点,$\therefore AB=\frac {1}{2}AC$,但不能证出$∠B=90^{\circ },\therefore $不能判定BC是$\odot A$的切线.故选D.
2.学科教材变式如图,$OA= OB= 13cm,AB= 24cm,\odot O$的直径为10cm.求证:AB是$\odot O$的切线.


答案:
证明 如图,过点O作$OC⊥AB$于点C,

$\because OA=OB=13cm,AB=24cm,\therefore AC=\frac {1}{2}AB=12cm$.在$Rt△OAC$中,根据勾股定理,得$OC=\sqrt {OA^{2}-AC^{2}}=5cm$.$\because \odot O$的直径为10 cm,$\therefore \odot O$的半径为5 cm,$\therefore OC$为$\odot O$的半径,$\because OC⊥AB,\therefore AB$是$\odot O$的切线.
证明 如图,过点O作$OC⊥AB$于点C,

$\because OA=OB=13cm,AB=24cm,\therefore AC=\frac {1}{2}AB=12cm$.在$Rt△OAC$中,根据勾股定理,得$OC=\sqrt {OA^{2}-AC^{2}}=5cm$.$\because \odot O$的直径为10 cm,$\therefore \odot O$的半径为5 cm,$\therefore OC$为$\odot O$的半径,$\because OC⊥AB,\therefore AB$是$\odot O$的切线.
3.「2025广东广州白云期末」如图,$\odot O$的直径AB的长为12,P是AB延长线上的一点,且$PB= 4$,C是$\odot O$上的一点,$PC= 8$.求证:PC是$\odot O$的切线.


答案:
证明 如图,连接OC,

$\because \odot O$的直径AB的长为12,$\therefore OB=OC=6$,
$\because PB=4,\therefore PO=PB+OB=4+6=10$,
$\because$ 在$△POC$中,$PC=8,OC=6,OP=10$,
$\therefore PC^{2}+OC^{2}=OP^{2},\therefore △POC$是直角三角形,$∠OCP=90^{\circ },\therefore OC⊥PC$,
$\because OC$是$\odot O$的半径,$\therefore PC$是$\odot O$的切线.
证明 如图,连接OC,

$\because \odot O$的直径AB的长为12,$\therefore OB=OC=6$,
$\because PB=4,\therefore PO=PB+OB=4+6=10$,
$\because$ 在$△POC$中,$PC=8,OC=6,OP=10$,
$\therefore PC^{2}+OC^{2}=OP^{2},\therefore △POC$是直角三角形,$∠OCP=90^{\circ },\therefore OC⊥PC$,
$\because OC$是$\odot O$的半径,$\therefore PC$是$\odot O$的切线.
4.「2024山西中考」如图,已知$\triangle ABC$,以AB为直径的$\odot O$交BC于点D,与AC相切于点A,连接OD.若$∠AOD= 80^{\circ }$,则$∠C$的度数为(

A.$30^{\circ }$
B.$40^{\circ }$
C.$45^{\circ }$
D.$50^{\circ }$
D
)
A.$30^{\circ }$
B.$40^{\circ }$
C.$45^{\circ }$
D.$50^{\circ }$
答案:D
$\because \widehat {AD}=\widehat {AD},\therefore ∠B=\frac {1}{2}∠AOD=40^{\circ }.\because $以AB为直径的$\odot O$与AC相切于点A,$\therefore ∠BAC=90^{\circ },\therefore ∠C=90^{\circ }-40^{\circ }=50^{\circ }$.故选D.
$\because \widehat {AD}=\widehat {AD},\therefore ∠B=\frac {1}{2}∠AOD=40^{\circ }.\because $以AB为直径的$\odot O$与AC相切于点A,$\therefore ∠BAC=90^{\circ },\therefore ∠C=90^{\circ }-40^{\circ }=50^{\circ }$.故选D.
5.「2025江苏南通海安月考」如图,$Rt\triangle ABC$中,$∠C= 90^{\circ },BC= 5$,点O在AB上,$OB= 3$,以OB为半径的$\odot O$与AC相切于点D,交BC于点E,则弦$BE= $____.


答案:
答案 4
解析 如图,连接OD,过点O作$OF⊥BC$于F,$\because AC$与$\odot O$相切于点D,$\therefore OD⊥AC,\because ∠C=90^{\circ },\therefore $四边形DOFC为矩形,$\therefore FC=OD=3,\therefore BF=BC-FC=5-3=2$,$\because OF⊥BE,\therefore BE=2BF=4$.
答案 4
解析 如图,连接OD,过点O作$OF⊥BC$于F,$\because AC$与$\odot O$相切于点D,$\therefore OD⊥AC,\because ∠C=90^{\circ },\therefore $四边形DOFC为矩形,$\therefore FC=OD=3,\therefore BF=BC-FC=5-3=2$,$\because OF⊥BE,\therefore BE=2BF=4$.

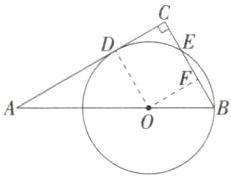
6.「2025黑龙江齐齐哈尔龙沙期中」如图,AB是$\odot O$的直径,点D是AB延长线上的一点,DC与$\odot O$相切于点C.连接BC,AC.
(1)求证:$∠A= ∠BCD$.
(2)若$∠D= 45^{\circ },\odot O$的半径为2,求线段AD的长.

(1)求证:$∠A= ∠BCD$.
(2)若$∠D= 45^{\circ },\odot O$的半径为2,求线段AD的长.

答案:
解析 (1)证明:如图,连接OC,$\because DC$是$\odot O$的切线,$\therefore ∠OCD=90^{\circ }$,即$∠BCD+∠OCB=90^{\circ }$,
$\because AB$是$\odot O$的直径,$\therefore ∠ACB=90^{\circ }$,
$\therefore ∠A+∠OBC=90^{\circ }$,
$\because OC=OB,\therefore ∠OCB=∠OBC,\therefore ∠A=∠BCD$.

(2)在$Rt△OCD$中,$∠D=45^{\circ },OC=2$,
$\therefore OA=OC=2,OD=\sqrt {2}OC=2\sqrt {2}$,
$\therefore AD=OA+OD=2+2\sqrt {2}$.
解析 (1)证明:如图,连接OC,$\because DC$是$\odot O$的切线,$\therefore ∠OCD=90^{\circ }$,即$∠BCD+∠OCB=90^{\circ }$,
$\because AB$是$\odot O$的直径,$\therefore ∠ACB=90^{\circ }$,
$\therefore ∠A+∠OBC=90^{\circ }$,
$\because OC=OB,\therefore ∠OCB=∠OBC,\therefore ∠A=∠BCD$.

(2)在$Rt△OCD$中,$∠D=45^{\circ },OC=2$,
$\therefore OA=OC=2,OD=\sqrt {2}OC=2\sqrt {2}$,
$\therefore AD=OA+OD=2+2\sqrt {2}$.
7.「2024山东济宁嘉祥期中,★☆」如图,在平面直角坐标系中,$\odot M$与x轴相切于点A,与y轴交于点B,C.若圆心M的坐标是$(4,5)$,则弦BC的长度为( )

A.3
B.4
C.5
D.6

A.3
B.4
C.5
D.6
答案:
D
如图,连接MA、MB、MC,过点M作$MN⊥y$轴,垂足为N,则$BN=CN=\frac {1}{2}BC,\because \odot M$与x轴相切于点A,$\therefore MA⊥x$轴,∵圆心M的坐标是$(4,5),\therefore MA=5$,
$MN=4,\therefore MB=MA=5$. 在$Rt△BMN$中,$BN=\sqrt {MB^{2}-MN^{2}}=\sqrt {5^{2}-4^{2}}=3,\therefore BC=2BN=6$.故选D.

D
如图,连接MA、MB、MC,过点M作$MN⊥y$轴,垂足为N,则$BN=CN=\frac {1}{2}BC,\because \odot M$与x轴相切于点A,$\therefore MA⊥x$轴,∵圆心M的坐标是$(4,5),\therefore MA=5$,
$MN=4,\therefore MB=MA=5$. 在$Rt△BMN$中,$BN=\sqrt {MB^{2}-MN^{2}}=\sqrt {5^{2}-4^{2}}=3,\therefore BC=2BN=6$.故选D.
