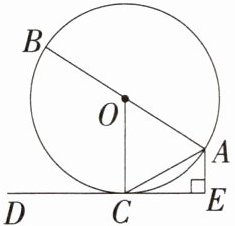
8.「2024河北衡水月考,★☆」如图,AB是$\odot O$的直径,C是$\odot O$上一点,D是$\odot O$外一点,过点A作$AE⊥CD$,垂足为E,连接OC,AC.若使CD切$\odot O$于点C,添加的下列条件中,不正确的是(
A.$OC// AE$
B.$∠OAC= ∠CAE$
C.$∠OCA= ∠CAE$
D.$OA= AC$
D
)
A.$OC// AE$
B.$∠OAC= ∠CAE$
C.$∠OCA= ∠CAE$
D.$OA= AC$
答案:D
A. $\because AE⊥CD,\therefore ∠AED=90^{\circ }$,当$OC// AE$时,$∠OCD=90^{\circ }$,即$OC⊥DE$,根据切线的判定,知CD切$\odot O$于点C,该选项正确,不符合题意;
B. $\because AE⊥CD,\therefore ∠AED=90^{\circ }$,则$∠CAE+∠ACE=90^{\circ },\because OA=OC,\therefore ∠OAC=∠OCA$,当$∠OAC=∠CAE$时,$∠OCA+∠ACE=90^{\circ }$,即$OC⊥DE$,根据切线的判定,知CD切$\odot O$于点C,该选项正确,不符合题意;
C. 当$∠OCA=∠CAE$时,$OC// AE,\because AE⊥CD,\therefore ∠AED=90^{\circ },\therefore ∠OCD=90^{\circ }$,即$OC⊥DE$,根据切线的判定,知CD切$\odot O$于点C,该选项正确,不符合题意;
D. 当$OA=AC$时,由$OA=OC$得到$OA=OC=AC$,则$△OAC$是等边三角形,无法确定$∠OCD=90^{\circ }$,不能得到CD切$\odot O$于点C,该选项不正确,符合题意.故选D.
A. $\because AE⊥CD,\therefore ∠AED=90^{\circ }$,当$OC// AE$时,$∠OCD=90^{\circ }$,即$OC⊥DE$,根据切线的判定,知CD切$\odot O$于点C,该选项正确,不符合题意;
B. $\because AE⊥CD,\therefore ∠AED=90^{\circ }$,则$∠CAE+∠ACE=90^{\circ },\because OA=OC,\therefore ∠OAC=∠OCA$,当$∠OAC=∠CAE$时,$∠OCA+∠ACE=90^{\circ }$,即$OC⊥DE$,根据切线的判定,知CD切$\odot O$于点C,该选项正确,不符合题意;
C. 当$∠OCA=∠CAE$时,$OC// AE,\because AE⊥CD,\therefore ∠AED=90^{\circ },\therefore ∠OCD=90^{\circ }$,即$OC⊥DE$,根据切线的判定,知CD切$\odot O$于点C,该选项正确,不符合题意;
D. 当$OA=AC$时,由$OA=OC$得到$OA=OC=AC$,则$△OAC$是等边三角形,无法确定$∠OCD=90^{\circ }$,不能得到CD切$\odot O$于点C,该选项不正确,符合题意.故选D.
9.易错题目「2025河南商丘柘城期中,★☆」如图,AB是$\odot O$的切线,B为切点,连接OA,与$\odot O$交于点C,D为$\odot O$上一动点(点D不与点C,B重合),连接CD,BD.若$∠A= 36^{\circ }$,则$∠D$的度数为____.


答案:
答案 $27^{\circ }$或$153^{\circ }$
解析 如图,连接OB,由切线性质可得$∠OBA=90^{\circ }$,$\because ∠A=36^{\circ },\therefore ∠COB=90^{\circ }-36^{\circ }=54^{\circ },\therefore ∠D=\frac {1}{2}∠COB=27^{\circ },\therefore ∠D'=180^{\circ }-27^{\circ }=153^{\circ }$.
综上,$∠D$的度数为$27^{\circ }$或$153^{\circ }$.

易错点 本题易忽略动点D在劣弧上的情况.
答案 $27^{\circ }$或$153^{\circ }$
解析 如图,连接OB,由切线性质可得$∠OBA=90^{\circ }$,$\because ∠A=36^{\circ },\therefore ∠COB=90^{\circ }-36^{\circ }=54^{\circ },\therefore ∠D=\frac {1}{2}∠COB=27^{\circ },\therefore ∠D'=180^{\circ }-27^{\circ }=153^{\circ }$.
综上,$∠D$的度数为$27^{\circ }$或$153^{\circ }$.

易错点 本题易忽略动点D在劣弧上的情况.
10.「2025黑龙江哈尔滨香坊期末,★☆」如图,四边形ABCD是$\odot O$的内接四边形,点O在四边形ABCD内部,过点C作$\odot O$的切线交AB的延长线于点P,连接OA,OB.若$∠AOB= 100^{\circ },∠BCP= 35^{\circ }$,则$∠ADC$的度数为____.


答案:
答案 $85^{\circ }$
解析 如图,连接OC,$\because PC$为$\odot O$的切线,$\therefore OC⊥PC$,$\therefore ∠OCP=90^{\circ },\therefore ∠OCB=90^{\circ }-∠BCP=90^{\circ }-35^{\circ }=55^{\circ },\because OC=OB,\therefore ∠OBC=∠OCB=55^{\circ }$,
$\because OA=OB,\therefore ∠OBA=∠OAB=\frac {1}{2}(180^{\circ }-∠AOB)=\frac {1}{2}×(180^{\circ }-100^{\circ })=40^{\circ },\therefore ∠ABC=∠OBA+∠OBC=40^{\circ }+55^{\circ }=95^{\circ },\because $四边形ABCD是$\odot O$的内接四边形,$\therefore ∠ADC+∠ABC=180^{\circ },\therefore ∠ADC=180^{\circ }-95^{\circ }=85^{\circ }$.

答案 $85^{\circ }$
解析 如图,连接OC,$\because PC$为$\odot O$的切线,$\therefore OC⊥PC$,$\therefore ∠OCP=90^{\circ },\therefore ∠OCB=90^{\circ }-∠BCP=90^{\circ }-35^{\circ }=55^{\circ },\because OC=OB,\therefore ∠OBC=∠OCB=55^{\circ }$,
$\because OA=OB,\therefore ∠OBA=∠OAB=\frac {1}{2}(180^{\circ }-∠AOB)=\frac {1}{2}×(180^{\circ }-100^{\circ })=40^{\circ },\therefore ∠ABC=∠OBA+∠OBC=40^{\circ }+55^{\circ }=95^{\circ },\because $四边形ABCD是$\odot O$的内接四边形,$\therefore ∠ADC+∠ABC=180^{\circ },\therefore ∠ADC=180^{\circ }-95^{\circ }=85^{\circ }$.

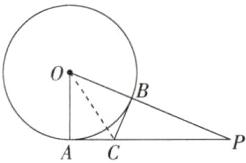
11.「2023河南中考,★☆」如图,PA与$\odot O$相切于点A,PO交$\odot O$于点B,点C在PA上,且$CB= CA$.若$OA= 5,PA= 12$,则CA的长为____.


答案:
答案 $\frac {10}{3}$
解析 如图,连接OC,$\because PA$与$\odot O$相切于点A,$\therefore ∠OAP=90^{\circ },\because OA=OB,OC=OC,CA=CB,\therefore △OAC\cong △OBC(SSS),\therefore ∠OAP=∠OBC=90^{\circ }$,在$Rt△OAP$中,$OA=5,PA=12,\therefore OP=\sqrt {OA^{2}+AP^{2}}=\sqrt {5^{2}+12^{2}}=13,\because S_{△OAC}+S_{△OCP}=S_{△OAP},\therefore \frac {1}{2}OA\cdot AC+\frac {1}{2}OP\cdot BC=\frac {1}{2}OA\cdot AP,\therefore OA\cdot AC+OP\cdot BC=OA\cdot AP,\therefore 5AC+13BC=5×12,\therefore AC=BC=\frac {10}{3}$.
答案 $\frac {10}{3}$
解析 如图,连接OC,$\because PA$与$\odot O$相切于点A,$\therefore ∠OAP=90^{\circ },\because OA=OB,OC=OC,CA=CB,\therefore △OAC\cong △OBC(SSS),\therefore ∠OAP=∠OBC=90^{\circ }$,在$Rt△OAP$中,$OA=5,PA=12,\therefore OP=\sqrt {OA^{2}+AP^{2}}=\sqrt {5^{2}+12^{2}}=13,\because S_{△OAC}+S_{△OCP}=S_{△OAP},\therefore \frac {1}{2}OA\cdot AC+\frac {1}{2}OP\cdot BC=\frac {1}{2}OA\cdot AP,\therefore OA\cdot AC+OP\cdot BC=OA\cdot AP,\therefore 5AC+13BC=5×12,\therefore AC=BC=\frac {10}{3}$.

12.「2024山东东营中考,★☆」如图,$\triangle ABC内接于\odot O$,AB是$\odot O$的直径,点E在$\odot O$上,点C是$\widehat {BE}$的中点,$AE⊥CD$,垂足为点D,DC的延长线交AB的延长线于点F.
(1)求证:CD是$\odot O$的切线.
(2)若$CD= \sqrt {3},∠ABC= 60^{\circ }$,求线段AF的长.

(1)求证:CD是$\odot O$的切线.
(2)若$CD= \sqrt {3},∠ABC= 60^{\circ }$,求线段AF的长.

答案:
解析 (1)证明:如图,连接OC,
$\because$ 点C是$\widehat {BE}$的中点,$\therefore \widehat {BC}=\widehat {CE},\therefore ∠BAC=∠CAE$,
$\because OC=OA,\therefore ∠OCA=∠OAC$,
$\therefore ∠OCA=∠CAD,\therefore OC// AD$,
$\because AE⊥CD,\therefore OC⊥DF$,
$\because OC$是$\odot O$的半径,$\therefore CD$是$\odot O$的切线.

(2)$\because AB$是$\odot O$的直径,$\therefore ∠ACB=90^{\circ }$,
$\because ∠ABC=60^{\circ },\therefore ∠BAC=30^{\circ },\therefore ∠CAD=∠BAC=30^{\circ },\therefore ∠BAD=∠BAC+∠CAD=60^{\circ }$.
$\because ∠D=90^{\circ },CD=\sqrt {3},\therefore AD=\sqrt {3}CD=3$,
$\because ∠F=180^{\circ }-∠D-∠BAD=30^{\circ },\therefore AF=2AD=6$.
解析 (1)证明:如图,连接OC,
$\because$ 点C是$\widehat {BE}$的中点,$\therefore \widehat {BC}=\widehat {CE},\therefore ∠BAC=∠CAE$,
$\because OC=OA,\therefore ∠OCA=∠OAC$,
$\therefore ∠OCA=∠CAD,\therefore OC// AD$,
$\because AE⊥CD,\therefore OC⊥DF$,
$\because OC$是$\odot O$的半径,$\therefore CD$是$\odot O$的切线.

(2)$\because AB$是$\odot O$的直径,$\therefore ∠ACB=90^{\circ }$,
$\because ∠ABC=60^{\circ },\therefore ∠BAC=30^{\circ },\therefore ∠CAD=∠BAC=30^{\circ },\therefore ∠BAD=∠BAC+∠CAD=60^{\circ }$.
$\because ∠D=90^{\circ },CD=\sqrt {3},\therefore AD=\sqrt {3}CD=3$,
$\because ∠F=180^{\circ }-∠D-∠BAD=30^{\circ },\therefore AF=2AD=6$.
13.「2024青海西宁中考,★☆」如图,PA,PB是$\odot O$的切线,A,B为切点,连接OA,OB,过点O作$OC// PA$交PB于点C,过点C作$CD⊥AP$,垂足为D.
(1)求证:$OC= AD$.
(2)若$\odot O$的半径是3,$PA= 9$,求OC的长.

(1)求证:$OC= AD$.
(2)若$\odot O$的半径是3,$PA= 9$,求OC的长.
5

答案:解析 (1)证明:$\because PA,PB$是$\odot O$的切线,OA,OB是$\odot O$的半径,$\therefore OA⊥PA,OB⊥PB$,
$\because OC// PA,CD⊥AP,\therefore CD⊥OC$,
$\therefore ∠OAD=∠CDA=∠OCD=90^{\circ }$,
$\therefore$ 四边形OADC是矩形,$\therefore OC=AD$.
(2)设$OC=AD=x$,
$\because$ 四边形OADC是矩形,$\odot O$的半径是3,$PA=9$,
$\therefore OA=OB=CD=3,PD=PA-AD=9-x$,
$\because OC// PA,\therefore ∠OCB=∠P$,
$\because OB⊥PB,CD⊥AP,\therefore ∠OBC=∠CDP=90^{\circ }$,
在$△OCB$和$△CPD$中,
$\begin{cases} ∠OCB=∠P \\ ∠OBC=∠CDP=90^{\circ } \\ OB=CD \end{cases}$
$\therefore △OCB\cong △CPD(AAS)$,
$\therefore BC=PD=9-x$,
在$Rt△OCB$中,由勾股定理得$OC^{2}=OB^{2}+BC^{2}$,
$\therefore x^{2}=3^{2}+(9-x)^{2}$,解得$x=5,\therefore OC=5$.
$\because OC// PA,CD⊥AP,\therefore CD⊥OC$,
$\therefore ∠OAD=∠CDA=∠OCD=90^{\circ }$,
$\therefore$ 四边形OADC是矩形,$\therefore OC=AD$.
(2)设$OC=AD=x$,
$\because$ 四边形OADC是矩形,$\odot O$的半径是3,$PA=9$,
$\therefore OA=OB=CD=3,PD=PA-AD=9-x$,
$\because OC// PA,\therefore ∠OCB=∠P$,
$\because OB⊥PB,CD⊥AP,\therefore ∠OBC=∠CDP=90^{\circ }$,
在$△OCB$和$△CPD$中,
$\begin{cases} ∠OCB=∠P \\ ∠OBC=∠CDP=90^{\circ } \\ OB=CD \end{cases}$
$\therefore △OCB\cong △CPD(AAS)$,
$\therefore BC=PD=9-x$,
在$Rt△OCB$中,由勾股定理得$OC^{2}=OB^{2}+BC^{2}$,
$\therefore x^{2}=3^{2}+(9-x)^{2}$,解得$x=5,\therefore OC=5$.