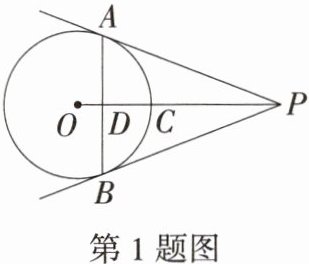
1.「2024福建厦门湖里期末」如图,PA,PB为⊙O的两条切线,切点分别为A,B,连接OP交⊙O于点C,交弦AB于点D.下列结论中错误的是(
A.PA= PB
B.OP⊥AB
C.$\overset{\frown}{AC}= \overset{\frown}{BC}$
D.△APB是等边三角形
D
)
A.PA= PB
B.OP⊥AB
C.$\overset{\frown}{AC}= \overset{\frown}{BC}$
D.△APB是等边三角形
答案:D 由切线长定理可得 $ PA = PB $,$ \angle APO = \angle BPO $,$ \therefore AB \perp OP $,$ AD = BD $,$ \therefore \overset{\frown}{AC} = \overset{\frown}{BC} $,故 A,B,C 正确,而 $ \triangle APB $ 中只满足 $ PA = PB $,无其他条件证明 $ \triangle APB $ 是等边三角形. 故选 D.
2.「2024江苏南通通州期中」如图,Rt△ABC中,∠C= 90°,O是边AC上一点,以O为圆心,OC长为半径的圆与边AB相切于点D.若BD= 5,AD= 8,则OC的长为(

A.$\frac{8}{3}$
B.$\frac{10}{3}$
C.$\frac{16}{3}$
D.$\frac{20}{3}$
B
)
A.$\frac{8}{3}$
B.$\frac{10}{3}$
C.$\frac{16}{3}$
D.$\frac{20}{3}$
答案:B 连接 $ OD $,$ \because \angle C = 90^{\circ} $,$ \therefore BC \perp OC $,$ \because OC $ 是 $ \odot O $ 的半径,$ \therefore BC $ 是 $ \odot O $ 的切线,$ \because \odot O $ 与 $ AB $ 相切于点 $ D $,$ BD = 5 $,$ AD = 8 $,$ \therefore BC = BD = 5 $,$ AB = BD + AD = 5 + 8 = 13 $,$ \therefore AC = \sqrt{AB^{2} - BC^{2}} = \sqrt{13^{2} - 5^{2}} = 12 $,$ \because AB \perp OD $,$ \therefore \angle ADO = 90^{\circ} $,$ \therefore AD^{2} + OD^{2} = OA^{2} $,$ \because OD = OC $,$ OA = 12 - OC $,$ \therefore 8^{2} + OC^{2} = (12 - OC)^{2} $,解得 $ OC = \frac{10}{3} $,故选 B.
3.「2024江苏盐城建湖期中」已知:点P是⊙O外一点.
(1)新尺规作图 尺规作图:如图,过点P作出⊙O的两条切线PA,PB,切点分别为A,B.(保留作图痕迹,不写作法)
(2)在(1)的条件下,若点C在⊙O上(点C不与A,B两点重合),且∠APB= 40°,则∠ACB的度数为______

(1)新尺规作图 尺规作图:如图,过点P作出⊙O的两条切线PA,PB,切点分别为A,B.(保留作图痕迹,不写作法)
(2)在(1)的条件下,若点C在⊙O上(点C不与A,B两点重合),且∠APB= 40°,则∠ACB的度数为______
70°或110°
.
答案:解析 (1) 如图所示.
提示:连接 $ OP $,作线段 $ OP $ 的垂直平分线,交 $ OP $ 于点 $ M $,再以点 $ M $ 为圆心,$ PM $ 的长为半径画圆,分别交 $ \odot O $ 于点 $ A $,$ B $,连接 $ PA $,$ PB $.
证明:连接 $ OA $,$ OB $,$ \because OP $ 为 $ \odot M $ 的直径,$ \therefore \angle OAP = \angle OBP = 90^{\circ} $,$ \therefore OA \perp AP $,$ OB \perp BP $,$ \because OA $,$ OB $ 为 $ \odot O $ 的半径,$ \therefore PA $,$ PB $ 为 $ \odot O $ 的切线,则 $ PA $,$ PB $ 即为所求.
(2) $ 70^{\circ} $ 或 $ 110^{\circ} $.
提示:连接 $ OA $,$ OB $,$ \because PA $,$ PB $ 为 $ \odot O $ 的两条切线,$ \therefore OA \perp PA $,$ OB \perp PB $,$ \therefore \angle OAP = \angle OBP = 90^{\circ} $,$ \because \angle APB = 40^{\circ} $,$ \therefore \angle AOB = 360^{\circ} - \angle OAP - \angle OBP - \angle APB = 140^{\circ} $.
当点 $ C $ 在优弧 $ AB $ 上时,$ \angle ACB = \frac{1}{2} \angle AOB = 70^{\circ} $.
当点 $ C $ 在劣弧 $ AB $ 上时,$ \angle ACB = 180^{\circ} - \frac{1}{2} \angle AOB = 110^{\circ} $. 综上所述,$ \angle ACB $ 的度数为 $ 70^{\circ} $ 或 $ 110^{\circ} $.
提示:连接 $ OP $,作线段 $ OP $ 的垂直平分线,交 $ OP $ 于点 $ M $,再以点 $ M $ 为圆心,$ PM $ 的长为半径画圆,分别交 $ \odot O $ 于点 $ A $,$ B $,连接 $ PA $,$ PB $.
证明:连接 $ OA $,$ OB $,$ \because OP $ 为 $ \odot M $ 的直径,$ \therefore \angle OAP = \angle OBP = 90^{\circ} $,$ \therefore OA \perp AP $,$ OB \perp BP $,$ \because OA $,$ OB $ 为 $ \odot O $ 的半径,$ \therefore PA $,$ PB $ 为 $ \odot O $ 的切线,则 $ PA $,$ PB $ 即为所求.
(2) $ 70^{\circ} $ 或 $ 110^{\circ} $.
提示:连接 $ OA $,$ OB $,$ \because PA $,$ PB $ 为 $ \odot O $ 的两条切线,$ \therefore OA \perp PA $,$ OB \perp PB $,$ \therefore \angle OAP = \angle OBP = 90^{\circ} $,$ \because \angle APB = 40^{\circ} $,$ \therefore \angle AOB = 360^{\circ} - \angle OAP - \angle OBP - \angle APB = 140^{\circ} $.
当点 $ C $ 在优弧 $ AB $ 上时,$ \angle ACB = \frac{1}{2} \angle AOB = 70^{\circ} $.
当点 $ C $ 在劣弧 $ AB $ 上时,$ \angle ACB = 180^{\circ} - \frac{1}{2} \angle AOB = 110^{\circ} $. 综上所述,$ \angle ACB $ 的度数为 $ 70^{\circ} $ 或 $ 110^{\circ} $.
4.「2023浙江湖州中考」如图,在Rt△ABC中,∠ACB= 90°,点O在边AC上,以点O为圆心,OC长为半径的半圆与斜边AB相切于点D,交OA于点E,连接OB.
(1)求证:BD= BC.
证明:∵∠ACB= 90°,OC为半圆O的半径,∴BC为半圆O的切线.∵半圆O与AB相切于点D,∴BD= BC.
(2)已知OC= 1,∠A= 30°,求AB的长.
(1)求证:BD= BC.
证明:∵∠ACB= 90°,OC为半圆O的半径,∴BC为半圆O的切线.∵半圆O与AB相切于点D,∴BD= BC.
(2)已知OC= 1,∠A= 30°,求AB的长.
2√3
答案:解析 (1) 证明:$ \because \angle ACB = 90^{\circ} $,$ CE $ 为半圆 $ O $ 的直径,$ \therefore BC $ 为半圆 $ O $ 的切线. $ \because $ 半圆 $ O $ 与 $ AB $ 相切于点 $ D $,$ \therefore BD = BC $.
(2) 连接 $ OD $ (图略),$ \because \angle A = 30^{\circ} $,$ \angle ACB = 90^{\circ} $,$ \therefore \angle ABC = 60^{\circ} $,易知 $ \text{Rt} \triangle ODB \cong \text{Rt} \triangle OCB $,$ \therefore \angle CBO = \angle DBO = \frac{1}{2} \angle ABC = 30^{\circ} $. 在 $ \text{Rt} \triangle OBC $ 中,$ OC = 1 $,$ \therefore OB = 2OC = 2 $,$ \therefore BC = \sqrt{2^{2} - 1^{2}} = \sqrt{3} $,在 $ \text{Rt} \triangle ABC $ 中,$ \angle A = 30^{\circ} $,$ \therefore AB = 2BC = 2\sqrt{3} $.
(2) 连接 $ OD $ (图略),$ \because \angle A = 30^{\circ} $,$ \angle ACB = 90^{\circ} $,$ \therefore \angle ABC = 60^{\circ} $,易知 $ \text{Rt} \triangle ODB \cong \text{Rt} \triangle OCB $,$ \therefore \angle CBO = \angle DBO = \frac{1}{2} \angle ABC = 30^{\circ} $. 在 $ \text{Rt} \triangle OBC $ 中,$ OC = 1 $,$ \therefore OB = 2OC = 2 $,$ \therefore BC = \sqrt{2^{2} - 1^{2}} = \sqrt{3} $,在 $ \text{Rt} \triangle ABC $ 中,$ \angle A = 30^{\circ} $,$ \therefore AB = 2BC = 2\sqrt{3} $.
5.「2023北京朝阳期末」用无刻度的直尺和圆规确定△ABC的内心,下列作法正确的是(

C
)
答案:C 三角形三条角平分线的交点即为三角形的内心.
6.「2025湖北武汉硚口月考」如图,⊙O是Rt△ABC的内切圆,∠C= 90°,AC= 3,AB= 5,则∠AOB的大小是______

135°
;⊙O的半径是______1
.
答案:答案 $ 135^{\circ} $;$ 1 $
解析 $ \because \angle C = 90^{\circ} $,$ \therefore \angle CAB + \angle CBA = 90^{\circ} $,$ \because \odot O $ 是 $ \text{Rt} \triangle ABC $ 的内切圆,$ \therefore \angle OAB = \frac{1}{2} \angle CAB $,$ \angle OBA = \frac{1}{2} \angle CBA $,$ \therefore \angle OAB + \angle OBA = 45^{\circ} $,$ \therefore \angle AOB = 180^{\circ} - (\angle OAB + \angle OBA) = 180^{\circ} - 45^{\circ} = 135^{\circ} $.
连接 $ OC $ (图略),$ \because \angle ACB = 90^{\circ} $,$ AC = 3 $,$ AB = 5 $,$ \therefore BC = \sqrt{AB^{2} - AC^{2}} = 4 $. 设 $ \odot O $ 的半径为 $ r $,$ \therefore S_{\triangle ABC} = \frac{1}{2} AC \times BC = \frac{1}{2} \times 3 \times 4 = 6 $,$ S_{\triangle ABC} = S_{\triangle AOC} + S_{\triangle BOC} + S_{\triangle AOB} = \frac{1}{2} AC \times r + \frac{1}{2} BC \times r + \frac{1}{2} AB \times r = \frac{1}{2} \times (3 + 4 + 5) r = 6r $,$ \therefore r = 1 $,即 $ \odot O $ 的半径为 $ 1 $.
方法解读:三角形的面积和内切圆半径的关系
由本题可得出结论:对于任意三角形,若该三角形周长为 $ C $,内切圆半径为 $ r $,面积为 $ S $,则有 $ S = \frac{1}{2} Cr $,亦可推得 $ r = \frac{2S}{C} $.
解析 $ \because \angle C = 90^{\circ} $,$ \therefore \angle CAB + \angle CBA = 90^{\circ} $,$ \because \odot O $ 是 $ \text{Rt} \triangle ABC $ 的内切圆,$ \therefore \angle OAB = \frac{1}{2} \angle CAB $,$ \angle OBA = \frac{1}{2} \angle CBA $,$ \therefore \angle OAB + \angle OBA = 45^{\circ} $,$ \therefore \angle AOB = 180^{\circ} - (\angle OAB + \angle OBA) = 180^{\circ} - 45^{\circ} = 135^{\circ} $.
连接 $ OC $ (图略),$ \because \angle ACB = 90^{\circ} $,$ AC = 3 $,$ AB = 5 $,$ \therefore BC = \sqrt{AB^{2} - AC^{2}} = 4 $. 设 $ \odot O $ 的半径为 $ r $,$ \therefore S_{\triangle ABC} = \frac{1}{2} AC \times BC = \frac{1}{2} \times 3 \times 4 = 6 $,$ S_{\triangle ABC} = S_{\triangle AOC} + S_{\triangle BOC} + S_{\triangle AOB} = \frac{1}{2} AC \times r + \frac{1}{2} BC \times r + \frac{1}{2} AB \times r = \frac{1}{2} \times (3 + 4 + 5) r = 6r $,$ \therefore r = 1 $,即 $ \odot O $ 的半径为 $ 1 $.
方法解读:三角形的面积和内切圆半径的关系
由本题可得出结论:对于任意三角形,若该三角形周长为 $ C $,内切圆半径为 $ r $,面积为 $ S $,则有 $ S = \frac{1}{2} Cr $,亦可推得 $ r = \frac{2S}{C} $.
7.「2023山东聊城中考,」如图,点O是△ABC外接圆的圆心,点I是△ABC的内心,连接OB,IA.若∠CAI= 35°,则∠OBC的度数为(

A.15°
B.17.5°
C.20°
D.25°
C
)
A.15°
B.17.5°
C.20°
D.25°
答案:C 如图,连接 $ OC $,$ \because $ 点 $ I $ 是 $ \triangle ABC $ 的内心,$ \therefore AI $ 平分 $ \angle BAC $,$ \because \angle CAI = 35^{\circ} $,$ \therefore \angle BAC = 2 \angle CAI = 70^{\circ} $,$ \because $ 点 $ O $ 是 $ \triangle ABC $ 外接圆的圆心,$ \therefore \angle BOC = 2 \angle BAC = 140^{\circ} $,$ \because OB = OC $,$ \therefore \angle OBC = \angle OCB = \frac{1}{2} \times (180^{\circ} - \angle BOC) = \frac{1}{2} \times (180^{\circ} - 140^{\circ}) = 20^{\circ} $. 故选 C.