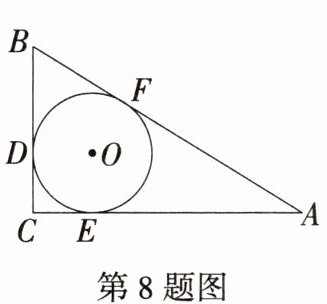
8.「2025贵州遵义红花岗期末,」如图,在Rt△ABC中,∠C= 90°,⊙O是△ABC的内切圆,三个切点分别为D,E,F,若BF= 4,AF= 6,则△ABC的面积是(
A.24
B.28
C.32
D.36
A
)
A.24
B.28
C.32
D.36
答案:A 如图,连接 $ DO $,$ EO $,$ \because \odot O $ 是 $ \triangle ABC $ 的内切圆,切点分别为 $ D $,$ E $,$ F $,$ \therefore OE \perp AC $,$ OD \perp BC $,$ CD = CE $,$ BD = BF = 4 $,$ AF = AE = 6 $,$ \therefore AB = AF + BF = 6 + 4 = 10 $,$ \because \angle C = 90^{\circ} $,$ \therefore $ 四边形 $ OECD $ 是矩形,又 $ \because EO = DO $,$ \therefore $ 矩形 $ OECD $ 是正方形,设 $ EO = x $,则 $ EC = CD = x $,在 $ \text{Rt} \triangle ABC $ 中,由勾股定理得 $ BC^{2} + AC^{2} = AB^{2} $,故 $ (x + 4)^{2} + (x + 6)^{2} = 10^{2} $,$ \therefore x = 2 $,$ \therefore BC = 6 $,$ AC = 8 $,$ \therefore S_{\triangle ABC} = \frac{1}{2} \times 6 \times 8 = 24 $. 故选 A.
9.学科对角互特色补模型「2025山东聊城期中改编,」如图,点I为△ABC的内心,AB= 7,AC= 9,∠BAC= 60°,连接AI并延长交△ABC的外接圆于点D,则AD的长为______

$\frac{16\sqrt{3}}{3}$
.
答案:答案 $ \frac{16\sqrt{3}}{3} $
解析 如图,连接 $ DB $,$ DC $,过 $ D $ 作 $ DE \perp AB $ 交 $ AB $ 的延长线于点 $ E $,$ DF \perp AC $ 于点 $ F $,$ \because $ 点 $ I $ 为 $ \triangle ABC $ 的内心,$ \angle BAC = 60^{\circ} $,$ \therefore \angle BAD = \angle CAD = 30^{\circ} $,$ \therefore BD = CD $,$ \because DE \perp AB $,$ DF \perp AC $,$ \therefore \angle DEB = \angle DFC = 90^{\circ} $,$ DE = DF $,$ \therefore \text{Rt} \triangle DEB \cong \text{Rt} \triangle DFC $,$ \text{Rt} \triangle ADE \cong \text{Rt} \triangle ADF $,$ \therefore EB = FC $,$ AE = AF $,又 $ \because AB = 7 $,$ AC = 9 $,$ \therefore AF = \frac{7 + 9}{2} = 8 $,在 $ \text{Rt} \triangle ADF $ 中,$ \angle CAD = 30^{\circ} $,$ \therefore DF = \frac{1}{2} AD $,由勾股定理得 $ DF^{2} + AF^{2} = AD^{2} $,即 $ \left( \frac{1}{2} AD \right)^{2} + 8^{2} = AD^{2} $,解得 $ AD = \frac{16\sqrt{3}}{3} $.
解析 如图,连接 $ DB $,$ DC $,过 $ D $ 作 $ DE \perp AB $ 交 $ AB $ 的延长线于点 $ E $,$ DF \perp AC $ 于点 $ F $,$ \because $ 点 $ I $ 为 $ \triangle ABC $ 的内心,$ \angle BAC = 60^{\circ} $,$ \therefore \angle BAD = \angle CAD = 30^{\circ} $,$ \therefore BD = CD $,$ \because DE \perp AB $,$ DF \perp AC $,$ \therefore \angle DEB = \angle DFC = 90^{\circ} $,$ DE = DF $,$ \therefore \text{Rt} \triangle DEB \cong \text{Rt} \triangle DFC $,$ \text{Rt} \triangle ADE \cong \text{Rt} \triangle ADF $,$ \therefore EB = FC $,$ AE = AF $,又 $ \because AB = 7 $,$ AC = 9 $,$ \therefore AF = \frac{7 + 9}{2} = 8 $,在 $ \text{Rt} \triangle ADF $ 中,$ \angle CAD = 30^{\circ} $,$ \therefore DF = \frac{1}{2} AD $,由勾股定理得 $ DF^{2} + AF^{2} = AD^{2} $,即 $ \left( \frac{1}{2} AD \right)^{2} + 8^{2} = AD^{2} $,解得 $ AD = \frac{16\sqrt{3}}{3} $.
10.「2024江苏盐城盐都期中,」如图,⊙O为△ABC的内切圆,切点分别为F、G、H,点D、E分别为BC、AC上的点,且DE为⊙O的切线.
(1)若∠C= 40°,求∠AOB的度数.
(2)若AC= 8,AB= 6,BC= 9,求△CDE的周长.
(1)若∠C= 40°,求∠AOB的度数.
110°
(2)若AC= 8,AB= 6,BC= 9,求△CDE的周长.
11
答案:解析 (1) $ \because \angle C = 40^{\circ} $,$ \therefore \angle ABC + \angle BAC = 180^{\circ} - 40^{\circ} = 140^{\circ} $,$ \because \odot O $ 为 $ \triangle ABC $ 的内切圆,$ \therefore \angle BAO = \angle CAO $,$ \angle ABO = \angle CBO $,$ \therefore \angle OAB + \angle OBA = \frac{1}{2} \times 140^{\circ} = 70^{\circ} $,$ \therefore \angle AOB = 180^{\circ} - 70^{\circ} = 110^{\circ} $.
(2) 设 $ DE $ 与 $ \odot O $ 相切于点 $ I $,如图,$ \because \odot O $ 为 $ \triangle ABC $ 的内切圆,$ DE $ 为 $ \odot O $ 的切线,$ \therefore EH = EI $,$ DI = DG $,$ \therefore \triangle CDE $ 的周长 $ = CD + CE + DE = CD + CE + EI + DI = CD + CE + EH + DG = CG + CH $. 易知 $ AF = AH $,$ BF = BG $,$ CG = CH $,$ \therefore CG + CH = (AB + BC + AC) - (AH + AF + BF + BG) = 6 + 9 + 8 - 2AB = 6 + 9 + 8 - 2 \times 6 = 11 $.
(2) 设 $ DE $ 与 $ \odot O $ 相切于点 $ I $,如图,$ \because \odot O $ 为 $ \triangle ABC $ 的内切圆,$ DE $ 为 $ \odot O $ 的切线,$ \therefore EH = EI $,$ DI = DG $,$ \therefore \triangle CDE $ 的周长 $ = CD + CE + DE = CD + CE + EI + DI = CD + CE + EH + DG = CG + CH $. 易知 $ AF = AH $,$ BF = BG $,$ CG = CH $,$ \therefore CG + CH = (AB + BC + AC) - (AH + AF + BF + BG) = 6 + 9 + 8 - 2AB = 6 + 9 + 8 - 2 \times 6 = 11 $.
11.「2024山东烟台中考,」如图,AB是⊙O的直径,△ABC内接于⊙O,点I为△ABC的内心,连接CI并延长交⊙O于点D.E是$\overset{\frown}{BC}$上任意一点,连接AD,BD,BE,CE.
(1)若∠ABC= 25°,求∠CEB的度数.
(2)找出图中所有与DI相等的线段,并证明.
(3)若CI= 2$\sqrt{2}$,DI= $\frac{13}{2}\sqrt{2}$,求△ABC的周长.

(1)若∠ABC= 25°,求∠CEB的度数.
115°
(2)找出图中所有与DI相等的线段,并证明.
AD,BD
(3)若CI= 2$\sqrt{2}$,DI= $\frac{13}{2}\sqrt{2}$,求△ABC的周长.
30

答案:解析 (1) $ \because AB $ 是 $ \odot O $ 的直径,$ \therefore \angle ADB = \angle ACB = 90^{\circ} $,又 $ \because \angle ABC = 25^{\circ} $,$ \therefore \angle CAB = 90^{\circ} - 25^{\circ} = 65^{\circ} $,$ \because $ 四边形 $ ABEC $ 是 $ \odot O $ 的内接四边形,$ \therefore \angle CEB + \angle CAB = 180^{\circ} $,$ \therefore \angle CEB = 180^{\circ} - \angle CAB = 115^{\circ} $.
(2) $ DI = AD = BD $. 证明如下:
如图,连接 $ AI $,
$ \because $ 点 $ I $ 为 $ \triangle ABC $ 的内心,$ \therefore \angle CAI = \angle BAI $,$ \angle ACI = \angle BCI = \frac{1}{2} \angle ACB = 45^{\circ} $,$ \therefore \overset{\frown}{AD} = \overset{\frown}{BD} $,$ \therefore \angle DAB = \angle DCB = \angle ACI $,$ AD = BD $,$ \because \angle DAI = \angle DAB + \angle BAI $,$ \angle DIA = \angle ACI + \angle CAI $,$ \therefore \angle DAI = \angle DIA $,$ \therefore DI = AD = BD $.
(3) 如图,过 $ I $ 分别作 $ IQ \perp AB $,$ IF \perp AC $,$ IP \perp BC $,垂足分别为 $ Q $,$ F $,$ P $,
$ \because $ 点 $ I $ 为 $ \triangle ABC $ 的内心,即点 $ I $ 为 $ \triangle ABC $ 的内切圆的圆心,$ \therefore Q $,$ F $,$ P $ 分别为该内切圆与 $ \triangle ABC $ 三边的切点,$ \therefore AQ = AF $,$ CF = CP $,$ BQ = BP $,$ \because CI = 2\sqrt{2} $,$ \angle IFC = 90^{\circ} $,$ \angle ACI = 45^{\circ} $,$ \therefore CF = CP = 2 $,$ \because DI = AD = BD $,$ DI = \frac{13}{2}\sqrt{2} $,$ \angle ADB = 90^{\circ} $,$ \therefore AB = \sqrt{AD^{2} + BD^{2}} = 13 $,$ \therefore \triangle ABC $ 的周长 $ = AB + AC + BC = AB + AF + CF + CP + BP = AB + AQ + BQ + 2CF = 2AB + 2CF = 2 \times 13 + 2 \times 2 = 30 $.
(2) $ DI = AD = BD $. 证明如下:
如图,连接 $ AI $,
$ \because $ 点 $ I $ 为 $ \triangle ABC $ 的内心,$ \therefore \angle CAI = \angle BAI $,$ \angle ACI = \angle BCI = \frac{1}{2} \angle ACB = 45^{\circ} $,$ \therefore \overset{\frown}{AD} = \overset{\frown}{BD} $,$ \therefore \angle DAB = \angle DCB = \angle ACI $,$ AD = BD $,$ \because \angle DAI = \angle DAB + \angle BAI $,$ \angle DIA = \angle ACI + \angle CAI $,$ \therefore \angle DAI = \angle DIA $,$ \therefore DI = AD = BD $.
(3) 如图,过 $ I $ 分别作 $ IQ \perp AB $,$ IF \perp AC $,$ IP \perp BC $,垂足分别为 $ Q $,$ F $,$ P $,
$ \because $ 点 $ I $ 为 $ \triangle ABC $ 的内心,即点 $ I $ 为 $ \triangle ABC $ 的内切圆的圆心,$ \therefore Q $,$ F $,$ P $ 分别为该内切圆与 $ \triangle ABC $ 三边的切点,$ \therefore AQ = AF $,$ CF = CP $,$ BQ = BP $,$ \because CI = 2\sqrt{2} $,$ \angle IFC = 90^{\circ} $,$ \angle ACI = 45^{\circ} $,$ \therefore CF = CP = 2 $,$ \because DI = AD = BD $,$ DI = \frac{13}{2}\sqrt{2} $,$ \angle ADB = 90^{\circ} $,$ \therefore AB = \sqrt{AD^{2} + BD^{2}} = 13 $,$ \therefore \triangle ABC $ 的周长 $ = AB + AC + BC = AB + AF + CF + CP + BP = AB + AQ + BQ + 2CF = 2AB + 2CF = 2 \times 13 + 2 \times 2 = 30 $.
12.新课标推理能力「2024四川内江中考」如图,在△ABC中,∠ABC= 60°,BC= 8,E是BC边上一点,且BE= 2,点I是△ABC的内心,BI的延长线交AC于点D,P是BD上一动点,连接PE,PC,则PE+PC的最小值为______

2√13
.
答案:答案 $ 2\sqrt{13} $
解析 如图,在 $ AB $ 上取点 $ F $,使 $ BF = BE = 2 $,连接 $ PF $,$ CF $,过点 $ F $ 作 $ FH \perp BC $ 于点 $ H $,$ \because $ 点 $ I $ 是 $ \triangle ABC $ 的内心,$ \therefore BI $ 平分 $ \angle ABC $,$ \therefore \angle ABD = \angle CBD $,又 $ BP = BP $,$ \therefore \triangle BFP \cong \triangle BEP (\text{SAS}) $,$ \therefore PF = PE $,$ \therefore PE + PC = PF + PC \geq CF $.
当 $ C $,$ P $,$ F $ 三点共线时,$ PE + PC $ 的值最小,最小值为 $ CF $ 的长,$ \because FH \perp BC $,$ \angle ABC = 60^{\circ} $,$ \therefore \angle BFH = 30^{\circ} $,$ \therefore BH = \frac{1}{2} BF = 1 $,$ \therefore FH = \sqrt{BF^{2} - BH^{2}} = \sqrt{3} $,$ CH = BC - BH = 7 $,$ \therefore CF = \sqrt{CH^{2} + FH^{2}} = 2\sqrt{13} $,$ \therefore PE + PC $ 的最小值为 $ 2\sqrt{13} $.
解析 如图,在 $ AB $ 上取点 $ F $,使 $ BF = BE = 2 $,连接 $ PF $,$ CF $,过点 $ F $ 作 $ FH \perp BC $ 于点 $ H $,$ \because $ 点 $ I $ 是 $ \triangle ABC $ 的内心,$ \therefore BI $ 平分 $ \angle ABC $,$ \therefore \angle ABD = \angle CBD $,又 $ BP = BP $,$ \therefore \triangle BFP \cong \triangle BEP (\text{SAS}) $,$ \therefore PF = PE $,$ \therefore PE + PC = PF + PC \geq CF $.
当 $ C $,$ P $,$ F $ 三点共线时,$ PE + PC $ 的值最小,最小值为 $ CF $ 的长,$ \because FH \perp BC $,$ \angle ABC = 60^{\circ} $,$ \therefore \angle BFH = 30^{\circ} $,$ \therefore BH = \frac{1}{2} BF = 1 $,$ \therefore FH = \sqrt{BF^{2} - BH^{2}} = \sqrt{3} $,$ CH = BC - BH = 7 $,$ \therefore CF = \sqrt{CH^{2} + FH^{2}} = 2\sqrt{13} $,$ \therefore PE + PC $ 的最小值为 $ 2\sqrt{13} $.