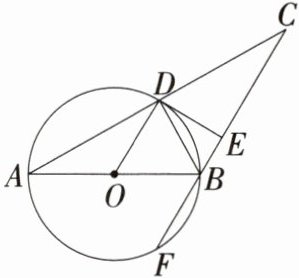
1. 「2025 湖南娄底娄星二模」如图,在$\triangle ABC$中,$AB = BC$,$AB为\odot O$的直径,$AC与\odot O相交于点D$,过点$D作DE\perp BC于点E$,$CB的延长线交\odot O于点F$,连接$OD$,$BD$。
(1) 求证:$DE为\odot O$的切线。
(2) 若$BE = 1$,$BF = 2$,求$AD$的长。
(1) 求证:$DE为\odot O$的切线。
(2) 若$BE = 1$,$BF = 2$,求$AD$的长。

答案:
解析
(1) 证明:∵ $ OA = OD $,∴ $ ∠A = ∠ADO $,
∵ $ AB = BC $,∴ $ ∠A = ∠C $,∴ $ ∠ADO = ∠C $,∴ $ OD // BC $。
∵ $ DE ⊥ BC $,∴ $ DE ⊥ OD $,
∵ $ OD $ 是 $ ⊙O $ 的半径,∴ $ DE $ 是 $ ⊙O $ 的切线。
(2) 如图,过点 $ O $ 作 $ OH ⊥ BF $ 于 $ H $,连接 $ OF $,则 $ ∠ODE = ∠DEH = ∠OHE = 90° $,
∴ 四边形 $ ODEH $ 是矩形,∴ $ OD = EH $,$ OH = DE $,
∵ $ OF = OB $,∴ $ BH = FH = 1 $,∴ $ OD = EH = OB = 2 $,
∴ $ AB = 2OD = 4 $,$ OH = \sqrt{OB^2 - BH^2} = \sqrt{3} $,
∴ $ DE = OH = \sqrt{3} $,∴ $ BD = \sqrt{DE^2 + BE^2} = 2 $,
∴ $ AD = \sqrt{AB^2 - BD^2} = \sqrt{4^2 - 2^2} = 2\sqrt{3} $。
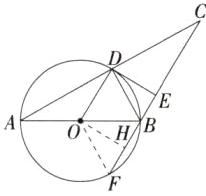
解析
(1) 证明:∵ $ OA = OD $,∴ $ ∠A = ∠ADO $,
∵ $ AB = BC $,∴ $ ∠A = ∠C $,∴ $ ∠ADO = ∠C $,∴ $ OD // BC $。
∵ $ DE ⊥ BC $,∴ $ DE ⊥ OD $,
∵ $ OD $ 是 $ ⊙O $ 的半径,∴ $ DE $ 是 $ ⊙O $ 的切线。
(2) 如图,过点 $ O $ 作 $ OH ⊥ BF $ 于 $ H $,连接 $ OF $,则 $ ∠ODE = ∠DEH = ∠OHE = 90° $,
∴ 四边形 $ ODEH $ 是矩形,∴ $ OD = EH $,$ OH = DE $,
∵ $ OF = OB $,∴ $ BH = FH = 1 $,∴ $ OD = EH = OB = 2 $,
∴ $ AB = 2OD = 4 $,$ OH = \sqrt{OB^2 - BH^2} = \sqrt{3} $,
∴ $ DE = OH = \sqrt{3} $,∴ $ BD = \sqrt{DE^2 + BE^2} = 2 $,
∴ $ AD = \sqrt{AB^2 - BD^2} = \sqrt{4^2 - 2^2} = 2\sqrt{3} $。

2. 「2024 山西吕梁交城期中」如图,$AB是\odot O$的直径,点$C$,$D是AB$同侧圆上两点,$AC = BD$,$AD与BC交于点E$,延长$AD到F$,使$DF = DE$,连接$BF$。
(1) 求证:$CE = DE$。
(2) 若$AD平分\angle BAC$,求证:$BF为\odot O$的切线。

(1) 求证:$CE = DE$。
证明:∵ $ AB $ 是 $ ⊙O $ 的直径,∴ $ ∠C = ∠ADB = 90° $。在 $ Rt△ABC $ 和 $ Rt△BAD $ 中,$ \begin{cases} AB = BA \\ AC = BD \end{cases} $,∴ $ Rt△ABC ≌ Rt△BAD(HL) $,∴ $ BC = AD $,$ ∠ABC = ∠BAD $,∴ $ AE = BE $,∴ $ CE = DE $。
(2) 若$AD平分\angle BAC$,求证:$BF为\odot O$的切线。
证明:∵ $ ∠ADB = 90° $,∴ $ BD ⊥ AF $,∵ $ DF = DE $,∴ $ BE = BF $,∴ $ ∠BEF = ∠F $。∵ $ AD $ 平分 $ ∠BAC $,∴ $ ∠CAE = ∠BAF $。∵ $ ∠C = 90° $,∴ $ ∠CAE + ∠AEC = 90° $。∵ $ ∠AEC = ∠BEF $,∴ $ ∠CAE + ∠BEF = 90° $,∴ $ ∠BAF + ∠F = 90° $,∴ $ ∠ABF = 90° $,∴ $ AB ⊥ BF $,∵ $ OB $ 是 $ ⊙O $ 的半径,∴ $ BF $ 是 $ ⊙O $ 的切线。

答案:证明
(1) ∵ $ AB $ 是 $ ⊙O $ 的直径,∴ $ ∠C = ∠ADB = 90° $。在 $ Rt△ABC $ 和 $ Rt△BAD $ 中,$ \begin{cases} AB = BA \\ AC = BD \end{cases} $,∴ $ Rt△ABC ≌ Rt△BAD(HL) $,∴ $ BC = AD $,$ ∠ABC = ∠BAD $,∴ $ AE = BE $,∴ $ CE = DE $。
(2) ∵ $ ∠ADB = 90° $,∴ $ BD ⊥ AF $,∵ $ DF = DE $,∴ $ BE = BF $,
∴ $ ∠BEF = ∠F $。∵ $ AD $ 平分 $ ∠BAC $,∴ $ ∠CAE = ∠BAF $。
∵ $ ∠C = 90° $,∴ $ ∠CAE + ∠AEC = 90° $。∵ $ ∠AEC = ∠BEF $,∴ $ ∠CAE + ∠BEF = 90° $,∴ $ ∠BAF + ∠F = 90° $,
∴ $ ∠ABF = 90° $,∴ $ AB ⊥ BF $,∵ $ OB $ 是 $ ⊙O $ 的半径,∴ $ BF $ 是 $ ⊙O $ 的切线。
(1) ∵ $ AB $ 是 $ ⊙O $ 的直径,∴ $ ∠C = ∠ADB = 90° $。在 $ Rt△ABC $ 和 $ Rt△BAD $ 中,$ \begin{cases} AB = BA \\ AC = BD \end{cases} $,∴ $ Rt△ABC ≌ Rt△BAD(HL) $,∴ $ BC = AD $,$ ∠ABC = ∠BAD $,∴ $ AE = BE $,∴ $ CE = DE $。
(2) ∵ $ ∠ADB = 90° $,∴ $ BD ⊥ AF $,∵ $ DF = DE $,∴ $ BE = BF $,
∴ $ ∠BEF = ∠F $。∵ $ AD $ 平分 $ ∠BAC $,∴ $ ∠CAE = ∠BAF $。
∵ $ ∠C = 90° $,∴ $ ∠CAE + ∠AEC = 90° $。∵ $ ∠AEC = ∠BEF $,∴ $ ∠CAE + ∠BEF = 90° $,∴ $ ∠BAF + ∠F = 90° $,
∴ $ ∠ABF = 90° $,∴ $ AB ⊥ BF $,∵ $ OB $ 是 $ ⊙O $ 的半径,∴ $ BF $ 是 $ ⊙O $ 的切线。
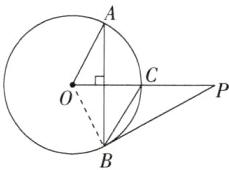
3. 「2024 广西防城港防城期末」已知$P是\odot O$外一点,$PO交\odot O于点C$,$OC = CP = 2$,弦$AB\perp OC$,$\angle AOC的度数为60^{\circ}$,连接$PB$、$BC$。
(1) 求$BC$的长。
(2) 求证:$PB是\odot O$的切线。

(1) 求$BC$的长。
(2) 求证:$PB是\odot O$的切线。

答案:
解析
(1) 如图,连接 $ OB $。
∵ $ AB ⊥ OC $,$ ∠AOC = 60° $,
∴ $ ∠OAB = 30° $。∵ $ OB = OA $,
∴ $ ∠OBA = ∠OAB = 30° $,
∴ $ ∠BOC = 60° $。∵ $ OB = OC $,
∴ $ △OBC $ 为等边三角形,∴ $ BC = OC $。∵ $ OC = 2 $,
∴ $ BC = 2 $。
(2) 证明:由(1)知,$ △OBC $ 为等边三角形,∴ $ ∠OBC = 60° $,∵ $ OC = CP $,∴ $ BC = PC $,∴ $ ∠P = ∠CBP $,∴ $ ∠OCB = 2∠CBP $,∵ $ ∠OCB = 60° $,∴ $ ∠CBP = 30° $,∴ $ ∠OBP = 90° $,即 $ OB ⊥ PB $,∵ $ OB $ 是 $ ⊙O $ 的半径,∴ $ PB $ 是 $ ⊙O $ 的切线。
解析
(1) 如图,连接 $ OB $。
∵ $ AB ⊥ OC $,$ ∠AOC = 60° $,
∴ $ ∠OAB = 30° $。∵ $ OB = OA $,
∴ $ ∠OBA = ∠OAB = 30° $,
∴ $ ∠BOC = 60° $。∵ $ OB = OC $,
∴ $ △OBC $ 为等边三角形,∴ $ BC = OC $。∵ $ OC = 2 $,
∴ $ BC = 2 $。
(2) 证明:由(1)知,$ △OBC $ 为等边三角形,∴ $ ∠OBC = 60° $,∵ $ OC = CP $,∴ $ BC = PC $,∴ $ ∠P = ∠CBP $,∴ $ ∠OCB = 2∠CBP $,∵ $ ∠OCB = 60° $,∴ $ ∠CBP = 30° $,∴ $ ∠OBP = 90° $,即 $ OB ⊥ PB $,∵ $ OB $ 是 $ ⊙O $ 的半径,∴ $ PB $ 是 $ ⊙O $ 的切线。

4. 「2025 河南许昌禹州期中」如图所示,$AB为半圆O$的直径,点$C$,$F$在半圆上,过点$C的直线与OF的延长线相交于点D$,与$AB的延长线相交于点P$,$AC与OF相交于点E$,$DC = DE$,$OD\perp AB$。
(1) 求证:$PC为半圆O$的切线。
(2) 若$OB = BP$,$AB = 4$,求点$C到AP$的距离。

(1) 求证:$PC为半圆O$的切线。
(2) 若$OB = BP$,$AB = 4$,求点$C到AP$的距离。

答案:
解析
(1) 证明:如图,连接 $ OC $,则 $ OC = OA $,
∴ $ ∠OCA = ∠A $,∵ $ DC = DE $,$ ∠DEC = ∠AEO $,
∴ $ ∠DCE = ∠DEC = ∠AEO $,∵ $ OD ⊥ AB $,∴ $ ∠AOE = 90° $,∴ $ ∠OCD = ∠OCA + ∠DCE = ∠A + ∠AEO = 90° $,
∴ $ PC ⊥ OC $,∵ $ OC $ 是半圆 $ O $ 的半径,∴ $ PC $ 为半圆 $ O $ 的切线。
(2) 如图,过点 $ C $ 作 $ CH ⊥ AP $ 于点 $ H $,∵ $ AB $ 是半圆 $ O $ 的直径,且 $ AB = 4 $,∴ $ OC = OB = \frac{1}{2}AB = 2 $,∵ $ OB = BP $,
∴ $ BP = 2 $,∴ $ OP = 4 $,∴ $ CP = \sqrt{OP^2 - OC^2} = \sqrt{4^2 - 2^2} = 2\sqrt{3} $,∵ $ S_{△OCP} = \frac{1}{2}OP \cdot CH = \frac{1}{2}CP \cdot OC $,∴ $ CH = \sqrt{3} $,
∴ 点 $ C $ 到 $ AP $ 的距离为 $ \sqrt{3} $。

解析
(1) 证明:如图,连接 $ OC $,则 $ OC = OA $,
∴ $ ∠OCA = ∠A $,∵ $ DC = DE $,$ ∠DEC = ∠AEO $,
∴ $ ∠DCE = ∠DEC = ∠AEO $,∵ $ OD ⊥ AB $,∴ $ ∠AOE = 90° $,∴ $ ∠OCD = ∠OCA + ∠DCE = ∠A + ∠AEO = 90° $,
∴ $ PC ⊥ OC $,∵ $ OC $ 是半圆 $ O $ 的半径,∴ $ PC $ 为半圆 $ O $ 的切线。
(2) 如图,过点 $ C $ 作 $ CH ⊥ AP $ 于点 $ H $,∵ $ AB $ 是半圆 $ O $ 的直径,且 $ AB = 4 $,∴ $ OC = OB = \frac{1}{2}AB = 2 $,∵ $ OB = BP $,
∴ $ BP = 2 $,∴ $ OP = 4 $,∴ $ CP = \sqrt{OP^2 - OC^2} = \sqrt{4^2 - 2^2} = 2\sqrt{3} $,∵ $ S_{△OCP} = \frac{1}{2}OP \cdot CH = \frac{1}{2}CP \cdot OC $,∴ $ CH = \sqrt{3} $,
∴ 点 $ C $ 到 $ AP $ 的距离为 $ \sqrt{3} $。

5. 「2024 江苏南京玄武期中」如图,在四边形$ABCD$中,$AC$,$BD相交于点E$,且$AB = AC = AD$,经过$A$,$C$,$D三点的\odot O交BD于点F$,连接$CF$。
(1) 求证:$CF = BF$。
(2) 若$CD = CB$,求证:$CB是\odot O$的切线。
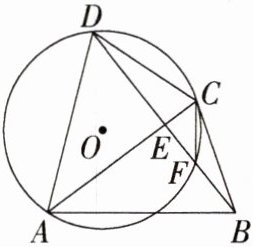
(1) 求证:$CF = BF$。
(2) 若$CD = CB$,求证:$CB是\odot O$的切线。

答案:
证明
(1) ∵ $ AB = AC $,∴ $ ∠ACB = ∠ABC $。∵ $ AB = AD $,
∴ $ ∠ADB = ∠ABD $,∵ $ ∠ADB = ∠ACF $,∴ $ ∠ACF = ∠ABD $,∴ $ ∠ACB - ∠ACF = ∠ABC - ∠ABD $,即 $ ∠BCF = ∠CBF $,∴ $ CF = BF $。
(2) 连接 $ CO $ 并延长交 $ ⊙O $ 于 $ G $ 点,连接 $ GF $,∵ $ CG $ 为 $ ⊙O $ 的直径,
∴ $ ∠GFC = 90° $,∴ $ ∠G + ∠GCF = 90° $。∵ $ ∠CDB = ∠G $,∴ $ ∠CDB + ∠GCF = 90° $。∵ $ CD = CB $,∴ $ ∠CDB = ∠CBD $。∵ $ ∠BCF = ∠CBD $,∴ $ ∠BCF = ∠CDB $,∴ $ ∠BCF + ∠GCF = 90° $,∴ $ ∠BCG = 90° $,∴ $ CG ⊥ BC $,∵ $ CG $ 为 $ ⊙O $ 的直径,∴ $ CB $ 是 $ ⊙O $ 的切线。

证明
(1) ∵ $ AB = AC $,∴ $ ∠ACB = ∠ABC $。∵ $ AB = AD $,
∴ $ ∠ADB = ∠ABD $,∵ $ ∠ADB = ∠ACF $,∴ $ ∠ACF = ∠ABD $,∴ $ ∠ACB - ∠ACF = ∠ABC - ∠ABD $,即 $ ∠BCF = ∠CBF $,∴ $ CF = BF $。
(2) 连接 $ CO $ 并延长交 $ ⊙O $ 于 $ G $ 点,连接 $ GF $,∵ $ CG $ 为 $ ⊙O $ 的直径,
∴ $ ∠GFC = 90° $,∴ $ ∠G + ∠GCF = 90° $。∵ $ ∠CDB = ∠G $,∴ $ ∠CDB + ∠GCF = 90° $。∵ $ CD = CB $,∴ $ ∠CDB = ∠CBD $。∵ $ ∠BCF = ∠CBD $,∴ $ ∠BCF = ∠CDB $,∴ $ ∠BCF + ∠GCF = 90° $,∴ $ ∠BCG = 90° $,∴ $ CG ⊥ BC $,∵ $ CG $ 为 $ ⊙O $ 的直径,∴ $ CB $ 是 $ ⊙O $ 的切线。
