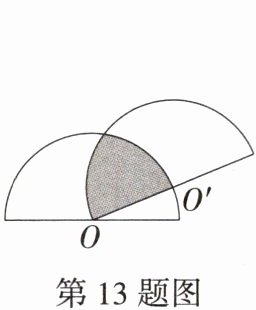
13.「2024山东泰安中考,★☆」两个半径相等的半圆按如图方式放置,半圆O'的一个直径端点与半圆O的圆心重合,若半圆的半径为2,则阴影部分的面积是( )
A.4/3π - √3
B.4/3π
C.2/3π - √3
D.4/3π - √3/4

A.4/3π - √3
B.4/3π
C.2/3π - √3
D.4/3π - √3/4
答案:
A 如图,设两个半圆的交点为 $A$,连接 $OA$,$AO'$,过点 $A$ 作 $AB \perp OO'$ 于点 $B$,$\because OA = OO' = AO' = 2$,$\therefore \triangle AOO'$ 是等边三角形,$\therefore \angle AOO' = 60^{\circ}$,$OB = \frac{1}{2}OO' = 1$,$\therefore AB = \sqrt{2^{2} - 1^{2}} = \sqrt{3}$,$\therefore S_{弓形AO'} = S_{扇形AOO'} - S_{\triangle AOO'} = \frac{60\pi \times 2^{2}}{360} - 2 \times \sqrt{3} \times \frac{1}{2} = \frac{2\pi}{3} - \sqrt{3}$,$\therefore S_{阴影} = S_{弓形AO'} + S_{扇形AO'O} = \frac{2\pi}{3} - \sqrt{3} + \frac{2\pi}{3} = \frac{4\pi}{3} - \sqrt{3}$。故选 A。

A 如图,设两个半圆的交点为 $A$,连接 $OA$,$AO'$,过点 $A$ 作 $AB \perp OO'$ 于点 $B$,$\because OA = OO' = AO' = 2$,$\therefore \triangle AOO'$ 是等边三角形,$\therefore \angle AOO' = 60^{\circ}$,$OB = \frac{1}{2}OO' = 1$,$\therefore AB = \sqrt{2^{2} - 1^{2}} = \sqrt{3}$,$\therefore S_{弓形AO'} = S_{扇形AOO'} - S_{\triangle AOO'} = \frac{60\pi \times 2^{2}}{360} - 2 \times \sqrt{3} \times \frac{1}{2} = \frac{2\pi}{3} - \sqrt{3}$,$\therefore S_{阴影} = S_{弓形AO'} + S_{扇形AO'O} = \frac{2\pi}{3} - \sqrt{3} + \frac{2\pi}{3} = \frac{4\pi}{3} - \sqrt{3}$。故选 A。

14.「2025河北石家庄裕华月考,★☆」如图,在

Rt△ABC中,∠C= 90°,∠ABC= 30°,AC= 1.将△ABC绕点B按顺时针方向旋转到△A'BC'的位置,使A,B,C'三点在同一直线上,则AB边扫过的面积为

Rt△ABC中,∠C= 90°,∠ABC= 30°,AC= 1.将△ABC绕点B按顺时针方向旋转到△A'BC'的位置,使A,B,C'三点在同一直线上,则AB边扫过的面积为
$\frac{5\pi}{3}$
.答案:答案 $\frac{5\pi}{3}$
解析 由旋转的性质得 $\angle A'BC' = \angle ABC = 30^{\circ}$,$\because A$,$B$,$C'$ 三点在同一直线上,$\therefore \angle ABA' = 180^{\circ} - \angle A'BC' = 150^{\circ}$,$\because$ 在 $Rt\triangle ABC$ 中,$\angle C = 90^{\circ}$,$\angle ABC = 30^{\circ}$,$AC = 1$,$\therefore AB = 2AC = 2$,$\therefore AB$ 边扫过的面积为 $\frac{150\pi \times 2^{2}}{360} = \frac{5\pi}{3}$。
解析 由旋转的性质得 $\angle A'BC' = \angle ABC = 30^{\circ}$,$\because A$,$B$,$C'$ 三点在同一直线上,$\therefore \angle ABA' = 180^{\circ} - \angle A'BC' = 150^{\circ}$,$\because$ 在 $Rt\triangle ABC$ 中,$\angle C = 90^{\circ}$,$\angle ABC = 30^{\circ}$,$AC = 1$,$\therefore AB = 2AC = 2$,$\therefore AB$ 边扫过的面积为 $\frac{150\pi \times 2^{2}}{360} = \frac{5\pi}{3}$。
15.「2023四川自贡中考,★☆」如图,小珍同学用半径为8 cm,圆心角为100°的扇形纸片,制作一个底面半径为2 cm的圆锥侧面,则圆锥上粘贴部分的面积是$______cm^2.$


答案:
答案 $\frac{16\pi}{9}$
解析 如图,由题意得 $\overparen{AC}$ 的长为 $2\pi \times 2 = 4\pi(cm)$,设 $\overparen{AC}$ 所对的圆心角为 $n^{\circ}$,则 $\frac{n\pi \times 8}{180} = 4\pi$,解得 $n = 90$,$\therefore$ 粘贴部分所对应的圆心角为 $100^{\circ} - 90^{\circ} = 10^{\circ}$,$\therefore$ 圆锥上粘贴部分的面积是 $\frac{10\pi \times 8^{2}}{360} = \frac{16\pi}{9}(cm^{2})$。

答案 $\frac{16\pi}{9}$
解析 如图,由题意得 $\overparen{AC}$ 的长为 $2\pi \times 2 = 4\pi(cm)$,设 $\overparen{AC}$ 所对的圆心角为 $n^{\circ}$,则 $\frac{n\pi \times 8}{180} = 4\pi$,解得 $n = 90$,$\therefore$ 粘贴部分所对应的圆心角为 $100^{\circ} - 90^{\circ} = 10^{\circ}$,$\therefore$ 圆锥上粘贴部分的面积是 $\frac{10\pi \times 8^{2}}{360} = \frac{16\pi}{9}(cm^{2})$。

16.「2025重庆沙坪坝期中,★☆」如图,长方形ABCD的长BC为4a,宽AB为2b,以点C为圆心,BC的长为半径作圆,与CD的延长线交于点E,以点A为圆心,AB的长为半径作圆,与AD交于点F,则阴影部分的面积为______.(结果保留π)


答案:
答案 $4\pi a^{2} + \pi b^{2} - 8ab$
解析 如图,设两个阴影部分的面积分别是 $S_{1}$,$S_{2}$,两个空白部分的面积分别是 $S_{3}$,$S_{4}$。根据图形,得 $S_{1} + S_{2} + S_{4} = S_{扇形BCE}$,$S_{1} + S_{3} = S_{扇形BAF}$,$S_{1} + S_{3} + S_{4} = S_{长方形ABCD}$,$\therefore S_{1} + S_{2} + S_{4} = \frac{90}{360}\pi \times (4a)^{2} = 4\pi a^{2}$ ①,$S_{1} + S_{3} = \frac{90}{360}\pi \times (2b)^{2} = \pi b^{2}$ ②,$S_{1} + S_{3} + S_{4} = 4a \cdot 2b = 8ab$ ③,把②代入③,得 $\pi b^{2} + S_{4} = 8ab$,解得 $S_{4} = 8ab - \pi b^{2}$ ④,把④代入①,得 $S_{1} + S_{2} + 8ab - \pi b^{2} = 4\pi a^{2}$,解得 $S_{1} + S_{2} = 4\pi a^{2} + \pi b^{2} - 8ab$,$\therefore$ 阴影部分的面积为 $4\pi a^{2} + \pi b^{2} - 8ab$。

答案 $4\pi a^{2} + \pi b^{2} - 8ab$
解析 如图,设两个阴影部分的面积分别是 $S_{1}$,$S_{2}$,两个空白部分的面积分别是 $S_{3}$,$S_{4}$。根据图形,得 $S_{1} + S_{2} + S_{4} = S_{扇形BCE}$,$S_{1} + S_{3} = S_{扇形BAF}$,$S_{1} + S_{3} + S_{4} = S_{长方形ABCD}$,$\therefore S_{1} + S_{2} + S_{4} = \frac{90}{360}\pi \times (4a)^{2} = 4\pi a^{2}$ ①,$S_{1} + S_{3} = \frac{90}{360}\pi \times (2b)^{2} = \pi b^{2}$ ②,$S_{1} + S_{3} + S_{4} = 4a \cdot 2b = 8ab$ ③,把②代入③,得 $\pi b^{2} + S_{4} = 8ab$,解得 $S_{4} = 8ab - \pi b^{2}$ ④,把④代入①,得 $S_{1} + S_{2} + 8ab - \pi b^{2} = 4\pi a^{2}$,解得 $S_{1} + S_{2} = 4\pi a^{2} + \pi b^{2} - 8ab$,$\therefore$ 阴影部分的面积为 $4\pi a^{2} + \pi b^{2} - 8ab$。

17.「2023江苏南通中考,★☆」如图,等腰三角形OAB的顶角∠AOB= 120°,⊙O和底边AB相切于点C,并与两腰OA,OB分别相交于D,E两点,连接CD,CE.
(1)求证:四边形ODCE是菱形.
(2)若⊙O的半径为2,求图中阴影部分的面积.

(1)求证:四边形ODCE是菱形.
(2)若⊙O的半径为2,求图中阴影部分的面积.

答案:
解析 (1) 证明:如图,连接 $OC$,$\because \odot O$ 和底边 $AB$ 相切于点 $C$,$\therefore OC \perp AB$。$\because OA = OB$,$\angle AOB = 120^{\circ}$,$\therefore \angle AOC = \angle BOC = \frac{1}{2}\angle AOB = 60^{\circ}$。$\because OD = OC$,$OC = OE$,$\therefore \triangle ODC$ 和 $\triangle OCE$ 都是等边三角形,$\therefore OD = OC = DC$,$OC = OE = CE$,$\therefore OD = CD = CE = OE$,$\therefore$ 四边形 $ODCE$ 是菱形。
(2) 如图,连接 $DE$ 交 $OC$ 于点 $F$,$\because$ 四边形 $ODCE$ 是菱形,$\therefore OF = \frac{1}{2}OC = 1$,$DE = 2DF$,$\angle OFD = 90^{\circ}$。在 $Rt\triangle ODF$ 中,$OD = 2$,$\therefore DF = \sqrt{OD^{2} - OF^{2}} = \sqrt{2^{2} - 1^{2}} = \sqrt{3}$,$\therefore DE = 2DF = 2\sqrt{3}$,$\therefore S_{阴影部分} = S_{扇形ODE} - S_{菱形ODCE} = \frac{120\pi \times 2^{2}}{360} - \frac{1}{2} \times 2 \times 2\sqrt{3} = \frac{4\pi}{3} - 2\sqrt{3}$,$\therefore$ 图中阴影部分的面积为 $\frac{4\pi}{3} - 2\sqrt{3}$。

解析 (1) 证明:如图,连接 $OC$,$\because \odot O$ 和底边 $AB$ 相切于点 $C$,$\therefore OC \perp AB$。$\because OA = OB$,$\angle AOB = 120^{\circ}$,$\therefore \angle AOC = \angle BOC = \frac{1}{2}\angle AOB = 60^{\circ}$。$\because OD = OC$,$OC = OE$,$\therefore \triangle ODC$ 和 $\triangle OCE$ 都是等边三角形,$\therefore OD = OC = DC$,$OC = OE = CE$,$\therefore OD = CD = CE = OE$,$\therefore$ 四边形 $ODCE$ 是菱形。
(2) 如图,连接 $DE$ 交 $OC$ 于点 $F$,$\because$ 四边形 $ODCE$ 是菱形,$\therefore OF = \frac{1}{2}OC = 1$,$DE = 2DF$,$\angle OFD = 90^{\circ}$。在 $Rt\triangle ODF$ 中,$OD = 2$,$\therefore DF = \sqrt{OD^{2} - OF^{2}} = \sqrt{2^{2} - 1^{2}} = \sqrt{3}$,$\therefore DE = 2DF = 2\sqrt{3}$,$\therefore S_{阴影部分} = S_{扇形ODE} - S_{菱形ODCE} = \frac{120\pi \times 2^{2}}{360} - \frac{1}{2} \times 2 \times 2\sqrt{3} = \frac{4\pi}{3} - 2\sqrt{3}$,$\therefore$ 图中阴影部分的面积为 $\frac{4\pi}{3} - 2\sqrt{3}$。

18.新学科动点最值问题「2023内蒙古通辽中考」如图,在扇形AOB中,∠AOB= 60°,OD平分∠AOB交⌢AB于点D,点C是半径OB上一动点,若OA= 1,则阴影部分周长的最小值为( )

A.√2 + π/6
B.√2 + π/3
C.2√2 + π/6
D.2√2 + π/3

A.√2 + π/6
B.√2 + π/3
C.2√2 + π/6
D.2√2 + π/3
答案:
A 如图,作 $D$ 点关于直线 $OB$ 的对称点 $E$,连接 $AE$,与 $OB$ 的交点为 $C$,此时阴影部分的周长最小,连接 $OE$,在扇形 $AOB$ 中,$\angle AOB = 60^{\circ}$,$OD$ 平分 $\angle AOB$ 交 $\overparen{AB}$ 于点 $D$,$\therefore \angle AOD = \angle BOD = 30^{\circ}$,由轴对称的性质,得 $\angle EOB = \angle BOD = 30^{\circ}$,$OE = OD$,$CD = CE$,$\therefore \angle AOE = 90^{\circ}$,$\therefore \triangle AOE$ 是等腰直角三角形,$\because OA = 1$,$\therefore AE = \sqrt{2}$,$\overparen{AD}$ 的长 $= \frac{30\pi \times 1}{180} = \frac{\pi}{6}$,$\therefore$ 阴影部分周长的最小值为 $\sqrt{2} + \frac{\pi}{6}$,故选 A。

A 如图,作 $D$ 点关于直线 $OB$ 的对称点 $E$,连接 $AE$,与 $OB$ 的交点为 $C$,此时阴影部分的周长最小,连接 $OE$,在扇形 $AOB$ 中,$\angle AOB = 60^{\circ}$,$OD$ 平分 $\angle AOB$ 交 $\overparen{AB}$ 于点 $D$,$\therefore \angle AOD = \angle BOD = 30^{\circ}$,由轴对称的性质,得 $\angle EOB = \angle BOD = 30^{\circ}$,$OE = OD$,$CD = CE$,$\therefore \angle AOE = 90^{\circ}$,$\therefore \triangle AOE$ 是等腰直角三角形,$\because OA = 1$,$\therefore AE = \sqrt{2}$,$\overparen{AD}$ 的长 $= \frac{30\pi \times 1}{180} = \frac{\pi}{6}$,$\therefore$ 阴影部分周长的最小值为 $\sqrt{2} + \frac{\pi}{6}$,故选 A。
