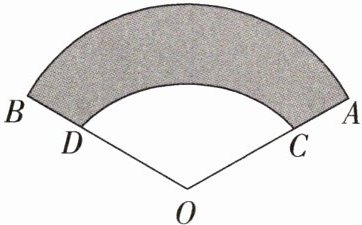
1. 学科 教材变式 特色 P116T8 「2023 四川雅安中考」如图,某小区要绿化一扇形 OAB 空地,准备在小扇形 OCD 内种花,在其余区域内(阴影部分)种草,测得$∠AOB = 120^{\circ}$,$OA = 15m$,$OC = 10m$,则种草区域的面积为 (
A.$\frac{25π}{3}m^{2}$
B.$\frac{125π}{3}m^{2}$
C.$\frac{250π}{3}m^{2}$
D.$\frac{125}{3}m^{2}$
$\frac{125π}{3}m²$
)
A.$\frac{25π}{3}m^{2}$
B.$\frac{125π}{3}m^{2}$
C.$\frac{250π}{3}m^{2}$
D.$\frac{125}{3}m^{2}$
答案:B S阴影=S扇形AOB−S扇形COD=$\frac{120π×15^2}{360}$−$\frac{120π×10^2}{360}$=$\frac{125π}{3}$(m²).故选B.
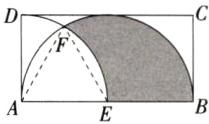
2.「2024 四川资阳中考」如图,在矩形 ABCD 中,$AB = 4$,$AD = 2$.以点 A 为圆心,AD 长为半径作弧交 AB 于点 E,再以 AB 为直径作半圆,与$\overset{\frown}{DE}$交于点 F,则图中阴影部分的面积为______.


答案:
答案$\sqrt{3}$+$\frac{2}{3}$π
解析 如图,连接AF、EF.由题意易知△AEF是等边三角形,∴S阴影=S半圆−S扇形AEF−S弓形AF=$\frac{1}{2}$×π×($\frac{4}{2}$)²−$\frac{60π×2^2}{360}$−($\frac{60π×2^2}{360}$−$\frac{1}{2}$×2×$\sqrt{3}$)=2π−$\frac{2}{3}$π−$\frac{2}{3}$π+$\sqrt{3}$=$\sqrt{3}$+$\frac{2}{3}$π.
答案$\sqrt{3}$+$\frac{2}{3}$π
解析 如图,连接AF、EF.由题意易知△AEF是等边三角形,∴S阴影=S半圆−S扇形AEF−S弓形AF=$\frac{1}{2}$×π×($\frac{4}{2}$)²−$\frac{60π×2^2}{360}$−($\frac{60π×2^2}{360}$−$\frac{1}{2}$×2×$\sqrt{3}$)=2π−$\frac{2}{3}$π−$\frac{2}{3}$π+$\sqrt{3}$=$\sqrt{3}$+$\frac{2}{3}$π.

3.「2024 重庆江津期末」如图,点 O 是以 AB 为直径的半圆的圆心,以 A 为圆心,AO 长为半径的弧交半圆于点 C,以 B 为圆心,BO 长为半径的弧交半圆于点 D,点 F 是$\overset{\frown}{CD}$上一点,$BF = 6$,$AF = 8$,则阴影部分的面积为

24 - $\frac{25π}{4}$
.(结果保留 π)
答案:答案 24 - $\frac{25π}{4}$
解析 ∵AB是半圆O的直径,∴∠AFB=90°,∴∠GAO+∠HBO=90°,AB=$\sqrt{AF^2+BF^2}$=10,∴OA=OB=AG=BH=5,∴S阴影部分=S△ABF−(S扇形AOG+S扇形OBH)=$\frac{1}{2}$×6×8−$\frac{90π×5^2}{360}$=24 - $\frac{25π}{4}$.
解析 ∵AB是半圆O的直径,∴∠AFB=90°,∴∠GAO+∠HBO=90°,AB=$\sqrt{AF^2+BF^2}$=10,∴OA=OB=AG=BH=5,∴S阴影部分=S△ABF−(S扇形AOG+S扇形OBH)=$\frac{1}{2}$×6×8−$\frac{90π×5^2}{360}$=24 - $\frac{25π}{4}$.
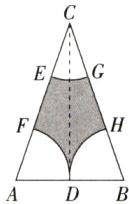
4. 学科 教材变式 特色 P123T7 「2023 山西太原模拟」如图,在$\triangle ABC$中,$CA = CB$,$AB = 4$,点 D 是 AB 的中点,分别以点 A,B,C 为圆心,AD 的长为半径画弧,交线段 AC,BC 于点 F,E,H,G,当点 E,F 是线段 AC 的三等分点时,图中阴影部分的面
积为 ( )

A.$8\sqrt{2} - 2π$
B.$16\sqrt{2} - 4π$
C.$8\sqrt{2} - 4π$
D.$16\sqrt{2} - 2π$
积为 ( )

A.$8\sqrt{2} - 2π$
B.$16\sqrt{2} - 4π$
C.$8\sqrt{2} - 4π$
D.$16\sqrt{2} - 2π$
答案:
A 如图,连接CD,∵CA=CB,点D是AB的中点,AB=4,∴CD⊥AB,AD=2,由题意可知AC=3AD=6,∴CD=$\sqrt{AC^2−AD^2}$=$\sqrt{6^2−2^2}$=4$\sqrt{2}$,∴S阴影=S△ABC−S扇形ADF−S扇形BDH−S扇形CEG=$\frac{1}{2}$×4×4$\sqrt{2}$−$\frac{180π×2^2}{360}$=8$\sqrt{2}$−2π.故选A.
A 如图,连接CD,∵CA=CB,点D是AB的中点,AB=4,∴CD⊥AB,AD=2,由题意可知AC=3AD=6,∴CD=$\sqrt{AC^2−AD^2}$=$\sqrt{6^2−2^2}$=4$\sqrt{2}$,∴S阴影=S△ABC−S扇形ADF−S扇形BDH−S扇形CEG=$\frac{1}{2}$×4×4$\sqrt{2}$−$\frac{180π×2^2}{360}$=8$\sqrt{2}$−2π.故选A.

5.「2025 重庆沙坪坝月考」如图所示的是半径为 5 的$\odot O$,直径$CD⊥AB$,$CD⊥EF$,点 F 为弧 BD 上一点,$FH⊥OB$,$∠EOD = 36^{\circ}$,则图中阴影部分的面积为 (

A. π
B. 5π
C.$\frac{5}{2}π$
D. 4π
C
)
A. π
B. 5π
C.$\frac{5}{2}π$
D. 4π
答案:C ∵CD⊥AB,CD⊥EF,∴AB//EF,EG=FG,∵FH⊥OB,∴四边形OGFH是矩形,∴OH=GF,∴OH=EG,∴四边形OEGH是平行四边形,∴S△OEG=S△OGH,∴S阴影=S扇形ODE=$\frac{36π×5^2}{360}$=$\frac{5}{2}$π.故选C.
6. 如图,CD 为大半圆的直径,O 为大半圆的圆心,小半圆的圆心$O_{1}$在线段 CD 上,大半圆的弦 AB 与小半圆交于点 E,F,$AB = 6cm$,$EF = 2cm$,且$AB// CD$,则阴影部分的面积为______$cm^{2}$.(结果保留 π)


答案:
答案4π
解析 如图,将两个半圆变为同心半圆,作OM⊥AB 于点M,连接OB,OF,则MF=$\frac{1}{2}$EF=1cm,BM=$\frac{1}{2}$AB=3cm,∴S阴影=$\frac{1}{2}$π·OB²−$\frac{1}{2}$π·OF²=$\frac{1}{2}$π(OB²−OF²)=$\frac{1}{2}$π[OM²+3²−(OM²+1²)]=4π(cm²).

答案4π
解析 如图,将两个半圆变为同心半圆,作OM⊥AB 于点M,连接OB,OF,则MF=$\frac{1}{2}$EF=1cm,BM=$\frac{1}{2}$AB=3cm,∴S阴影=$\frac{1}{2}$π·OB²−$\frac{1}{2}$π·OF²=$\frac{1}{2}$π(OB²−OF²)=$\frac{1}{2}$π[OM²+3²−(OM²+1²)]=4π(cm²).

7.「2024 四川成都模拟」如图,在$Rt\triangle ABC$中,$AC = BC = 2\sqrt{2}$,$∠ACB = 90^{\circ}$,D 是 AB 的中点,以点 D 为圆心,作圆心角为$90^{\circ}$的扇形 DEF,点 C 恰好在$\overset{\frown}{EF}$上(点 E,F 不与点 C 重合),半径 DE,DF 分别与 AC,BC 相交于点 G,H,则阴影部分的面积为______.


答案:
答案 π - 2
解析 如图,连接CD,作DM⊥AC于M,DN⊥BC 于N,∵∠ACB=90°,DM⊥AC,DN⊥BC,∴四边形DMCN是矩形,∠MDN=90°,又∵∠EDF=90°,∴∠MDG=∠NDH=90°−∠EDN,在Rt△ABC中,AC=BC=2$\sqrt{2}$,∴AB=$\sqrt{AC^2+BC^2}$=4,∵D是AB的中点,∴CD=$\frac{1}{2}$AB=2,由DM⊥AC,∠ACB=90°可知MD//BC,∴MD=$\frac{1}{2}$BC=$\sqrt{2}$,同理可得DN=$\frac{1}{2}$AC=$\sqrt{2}$,∴DM=DN,在△DMG和△DNH中,$\begin{cases} \angle MDG = \angle NDH \\ DM = DN \\ \angle DMG = \angle DNH = 90^{\circ} \end{cases}$,∴△DMG≌△DNH(ASA),∴S四边形DGCH=S矩形DMCN=$\sqrt{2}$×$\sqrt{2}$=2,∴S阴影=S扇形EDF−S四边形DGCH=$\frac{90π×2^2}{360}$ - 2=π - 2.

答案 π - 2
解析 如图,连接CD,作DM⊥AC于M,DN⊥BC 于N,∵∠ACB=90°,DM⊥AC,DN⊥BC,∴四边形DMCN是矩形,∠MDN=90°,又∵∠EDF=90°,∴∠MDG=∠NDH=90°−∠EDN,在Rt△ABC中,AC=BC=2$\sqrt{2}$,∴AB=$\sqrt{AC^2+BC^2}$=4,∵D是AB的中点,∴CD=$\frac{1}{2}$AB=2,由DM⊥AC,∠ACB=90°可知MD//BC,∴MD=$\frac{1}{2}$BC=$\sqrt{2}$,同理可得DN=$\frac{1}{2}$AC=$\sqrt{2}$,∴DM=DN,在△DMG和△DNH中,$\begin{cases} \angle MDG = \angle NDH \\ DM = DN \\ \angle DMG = \angle DNH = 90^{\circ} \end{cases}$,∴△DMG≌△DNH(ASA),∴S四边形DGCH=S矩形DMCN=$\sqrt{2}$×$\sqrt{2}$=2,∴S阴影=S扇形EDF−S四边形DGCH=$\frac{90π×2^2}{360}$ - 2=π - 2.
