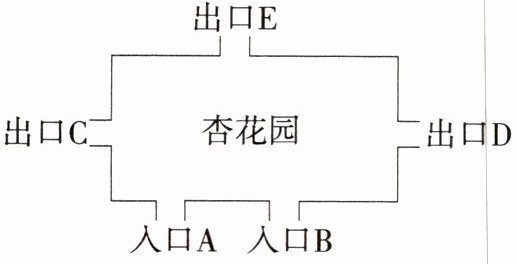
8. 「2025广东深圳月考,★☆」小明去“满阶芳草绿,一片杏花香”的杏花园赏花.如图,杏花园有两个入口、三个出口,则嘉嘉从入口B进入,从出口D离开的概率为(
A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{4}$
D. $\frac{1}{6}$
$\frac{1}{6}$
)
A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{4}$
D. $\frac{1}{6}$
答案:D 列表如下:
| | C | D | E |
| --- | --- | --- | --- |
| A | (A,C) | (A,D) | (A,E) |
| B | (B,C) | (B,D) | (B,E) |
共有6种等可能的结果,其中嘉嘉从入口B进入,从出口D离开的结果有1种,∴嘉嘉从入口B进入,从出口D离开的概率为$\frac{1}{6}$。故选D。
| | C | D | E |
| --- | --- | --- | --- |
| A | (A,C) | (A,D) | (A,E) |
| B | (B,C) | (B,D) | (B,E) |
共有6种等可能的结果,其中嘉嘉从入口B进入,从出口D离开的结果有1种,∴嘉嘉从入口B进入,从出口D离开的概率为$\frac{1}{6}$。故选D。
9. 「2024山东东营中考,★☆」如图,四边形ABCD是平行四边形,从①$AC = BD$,②$AC \perp BD$,③$AB = BC$这三个条件中任意选取两个,能使$□ ABCD$是正方形的概率为(

A. $\frac{2}{3}$
B. $\frac{1}{2}$
C. $\frac{1}{3}$
D. $\frac{5}{6}$
A
)
A. $\frac{2}{3}$
B. $\frac{1}{2}$
C. $\frac{1}{3}$
D. $\frac{5}{6}$
答案:A 列表如下:
| | ① | ② | ③ |
| --- | --- | --- | --- |
| ① | — | ①② | ①③ |
| ② | ②① | — | ②③ |
| ③ | ③① | ③② | — |
共有6种等可能的结果,其中能使□ABCD是正方形的结果有①②,①③,②①,③①,共4种,∴能使□ABCD是正方形的概率为$\frac{4}{6}=\frac{2}{3}$。故选A。
| | ① | ② | ③ |
| --- | --- | --- | --- |
| ① | — | ①② | ①③ |
| ② | ②① | — | ②③ |
| ③ | ③① | ③② | — |
共有6种等可能的结果,其中能使□ABCD是正方形的结果有①②,①③,②①,③①,共4种,∴能使□ABCD是正方形的概率为$\frac{4}{6}=\frac{2}{3}$。故选A。
10. 跨电路「2024四川内江中考,★☆」如图所示的电路中,当随机闭合开关$S_1$,$S_2$,$S_3$中的两个时,灯泡能发光的概率为(

A. $\frac{2}{3}$
B. $\frac{1}{2}$
C. $\frac{1}{3}$
D. $\frac{1}{6}$
A
)
A. $\frac{2}{3}$
B. $\frac{1}{2}$
C. $\frac{1}{3}$
D. $\frac{1}{6}$
答案:A 列表如下:
| | S₁ | S₂ | S₃ |
| --- | --- | --- | --- |
| S₁ | — | (S₁,S₂) | (S₁,S₃) |
| S₂ | (S₂,S₁) | — | (S₂,S₃) |
| S₃ | (S₃,S₁) | (S₃,S₂) | — |
共有6种等可能的结果,其中灯泡能发光的结果有4种,即(S₁,S₂),(S₁,S₃),(S₂,S₁),(S₃,S₁),∴灯泡能发光的概率为$\frac{4}{6}=\frac{2}{3}$。故选A。
| | S₁ | S₂ | S₃ |
| --- | --- | --- | --- |
| S₁ | — | (S₁,S₂) | (S₁,S₃) |
| S₂ | (S₂,S₁) | — | (S₂,S₃) |
| S₃ | (S₃,S₁) | (S₃,S₂) | — |
共有6种等可能的结果,其中灯泡能发光的结果有4种,即(S₁,S₂),(S₁,S₃),(S₂,S₁),(S₃,S₁),∴灯泡能发光的概率为$\frac{4}{6}=\frac{2}{3}$。故选A。
11. 「2022山东聊城中考,★☆」如图,有两个相同的可以自由转动的转盘A和B,转盘A被三等分,分别标有数字2,0,-1;转盘B被四等分,分别标有数字3,2,-2,-3.如果同时转动转盘A,B,转盘停止时,两个指针指向转盘A,B上的对应数字分别为x,y(当指针指在两个扇形的交线时,需重新转动转盘),那么点$(x,y)$落在直角坐标系第二象限的概率是


$\frac{1}{6}$
.答案:答案 $\frac{1}{6}$
解析 列表如下:
| | 2 | 0 | -1 |
| --- | --- | --- | --- |
| 3 | (2,3) | (0,3) | (-1,3) |
| 2 | (2,2) | (0,2) | (-1,2) |
| -2 | (2,-2) | (0,-2) | (-1,-2) |
| -3 | (2,-3) | (0,-3) | (-1,-3) |
由表可知,共有12种等可能的结果,其中点(x,y)落在直角坐标系第二象限的结果有2种,所以点(x,y)落在直角坐标系第二象限的概率是$\frac{2}{12}=\frac{1}{6}$。
解析 列表如下:
| | 2 | 0 | -1 |
| --- | --- | --- | --- |
| 3 | (2,3) | (0,3) | (-1,3) |
| 2 | (2,2) | (0,2) | (-1,2) |
| -2 | (2,-2) | (0,-2) | (-1,-2) |
| -3 | (2,-3) | (0,-3) | (-1,-3) |
由表可知,共有12种等可能的结果,其中点(x,y)落在直角坐标系第二象限的结果有2种,所以点(x,y)落在直角坐标系第二象限的概率是$\frac{2}{12}=\frac{1}{6}$。
12. 「2024广东佛山月考,★☆」“天宫课堂”第三课开讲,航天员陈冬、刘洋、蔡旭哲相互配合进行授课,激发了同学们学习航天知识的热情.在学校组织的航天知识竞赛中,小明和小雪均获得了一等奖,学校决定通过两人做游戏的方式,从中选取一名游戏获胜的同学作为代表分享获奖心得.游戏规则如下:甲口袋(不透明)装有编号为1,2,3的三个小球,乙口袋(不透明)装有编号为1,2,3,4的四个小球,每个口袋中的小球除编号外其他都相同.小明先从甲口袋中随机摸出一个球,小雪再从乙口袋中随机摸出一个球,若两球编号之和为偶数,则小明获胜;若两球编号之和为奇数,则小雪获胜.
(1)小明摸到小球的编号为2的概率为______
(2)请说明这个游戏对双方是否公平.
根据题意列表如下:
| 小雪和小明 | 1 | 2 | 3 | 4 |
| --- | --- | --- | --- | --- |
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 5 | 6 |
| 3 | 4 | 5 | 6 | 7 |
由表格知,共有12种等可能的结果,其中两球编号之和为偶数的结果有6种,两球编号之和为奇数的结果有6种,则小明获胜的概率是$\frac{1}{2}$,小雪获胜的概率是$\frac{1}{2}$,∵$\frac{1}{2}=\frac{1}{2}$,∴这个游戏对双方公平.
(1)小明摸到小球的编号为2的概率为______
$\frac{1}{3}$
.(2)请说明这个游戏对双方是否公平.
根据题意列表如下:
| 小雪和小明 | 1 | 2 | 3 | 4 |
| --- | --- | --- | --- | --- |
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 5 | 6 |
| 3 | 4 | 5 | 6 | 7 |
由表格知,共有12种等可能的结果,其中两球编号之和为偶数的结果有6种,两球编号之和为奇数的结果有6种,则小明获胜的概率是$\frac{1}{2}$,小雪获胜的概率是$\frac{1}{2}$,∵$\frac{1}{2}=\frac{1}{2}$,∴这个游戏对双方公平.
答案:解析 (1)$\frac{1}{3}$。
(2)根据题意列表如下:
| 小雪和小明 | 1 | 2 | 3 | 4 |
| --- | --- | --- | --- | --- |
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 5 | 6 |
| 3 | 4 | 5 | 6 | 7 |
由表格知,共有12种等可能的结果,其中两球编号之和为偶数的结果有6种,两球编号之和为奇数的结果有6种,则小明获胜的概率是$\frac{1}{2}$,小雪获胜的概率是$\frac{1}{2}$,∵$\frac{1}{2}=\frac{1}{2}$,∴这个游戏对双方公平。
方法总结 求出双方获胜的概率,若概率相等,则公平;若概率不相等,则不公平。
(2)根据题意列表如下:
| 小雪和小明 | 1 | 2 | 3 | 4 |
| --- | --- | --- | --- | --- |
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 5 | 6 |
| 3 | 4 | 5 | 6 | 7 |
由表格知,共有12种等可能的结果,其中两球编号之和为偶数的结果有6种,两球编号之和为奇数的结果有6种,则小明获胜的概率是$\frac{1}{2}$,小雪获胜的概率是$\frac{1}{2}$,∵$\frac{1}{2}=\frac{1}{2}$,∴这个游戏对双方公平。
方法总结 求出双方获胜的概率,若概率相等,则公平;若概率不相等,则不公平。