11. 某公司营销人员的月收入与每月的销售量成一次函数关系,已知销售 1 万件时,收入为 800 元,销售 3 万件时,收入为 1600 元,那么没有销售量时,收入为
400
元。答案:400
12. (2024·泰兴期末)如图,在平面直角坐标系中,$ A(2,0) $,$ B(0,4) $。
(1) 求直线 $ AB $ 的函数表达式;
(2) 点 $ D $ 在线段 $ AB $ 上,过点 $ D $ 作 $ DC // y $ 轴交 $ x $ 轴于点 $ C $,过点 $ C $ 作 $ CE // AB $ 交 $ y $ 轴于点 $ E $,若 $ BE = \frac{3}{2} $,求点 $ D $ 的坐标。
(1)设直线 $ AB $ 的函数表达式为 $ y = kx + b $,
则
$\begin{cases}2k + b = 0, \\b = 4,\end{cases}$
解得
$\begin{cases}k =
所以一次函数的表达式为 $ y =
(2)因为 $ CD // y $ 轴,$ CE // AB $,
所以四边形 $ CDBE $ 是平行四边形。
所以 $ CD = BE = \frac{3}{2} $,则点 $ D $ 的纵坐标为 $
将 $ y = \frac{3}{2} $ 代入函数表达式得,$ -2x + 4 = \frac{3}{2} $,解得 $ x =
所以点 $ D $ 的坐标为 $
(1) 求直线 $ AB $ 的函数表达式;
(2) 点 $ D $ 在线段 $ AB $ 上,过点 $ D $ 作 $ DC // y $ 轴交 $ x $ 轴于点 $ C $,过点 $ C $ 作 $ CE // AB $ 交 $ y $ 轴于点 $ E $,若 $ BE = \frac{3}{2} $,求点 $ D $ 的坐标。
(1)设直线 $ AB $ 的函数表达式为 $ y = kx + b $,
则
$\begin{cases}2k + b = 0, \\b = 4,\end{cases}$
解得
$\begin{cases}k =
-2
, \\b = 4
,\end{cases}$所以一次函数的表达式为 $ y =
-2x + 4
$。(2)因为 $ CD // y $ 轴,$ CE // AB $,
所以四边形 $ CDBE $ 是平行四边形。
所以 $ CD = BE = \frac{3}{2} $,则点 $ D $ 的纵坐标为 $
\frac{3}{2}
$。将 $ y = \frac{3}{2} $ 代入函数表达式得,$ -2x + 4 = \frac{3}{2} $,解得 $ x =
\frac{5}{4}
$。所以点 $ D $ 的坐标为 $
(\frac{5}{4}, \frac{3}{2})
$。答案:解:(1)设直线 $ AB $ 的函数表达式为 $ y = kx + b $,
则
$\begin{cases}2k + b = 0, \\b = 4,\end{cases}$
解得
$\begin{cases}k = -2, \\b = 4,\end{cases}$
所以一次函数的表达式为 $ y = -2x + 4 $。
(2)因为 $ CD // y $ 轴,$ CE // AB $,
所以四边形 $ CDBE $ 是平行四边形。
所以 $ CD = BE = \frac{3}{2} $,则点 $ D $ 的纵坐标为 $ \frac{3}{2} $。
将 $ y = \frac{3}{2} $ 代入函数表达式得,$ -2x + 4 = \frac{3}{2} $,解得 $ x = \frac{5}{4} $。
所以点 $ D $ 的坐标为 $ (\frac{5}{4}, \frac{3}{2}) $。
则
$\begin{cases}2k + b = 0, \\b = 4,\end{cases}$
解得
$\begin{cases}k = -2, \\b = 4,\end{cases}$
所以一次函数的表达式为 $ y = -2x + 4 $。
(2)因为 $ CD // y $ 轴,$ CE // AB $,
所以四边形 $ CDBE $ 是平行四边形。
所以 $ CD = BE = \frac{3}{2} $,则点 $ D $ 的纵坐标为 $ \frac{3}{2} $。
将 $ y = \frac{3}{2} $ 代入函数表达式得,$ -2x + 4 = \frac{3}{2} $,解得 $ x = \frac{5}{4} $。
所以点 $ D $ 的坐标为 $ (\frac{5}{4}, \frac{3}{2}) $。
13. $ y_1 $ 与 $ x + 1 $ 成正比例,$ y_2 $ 与 $ x - 1 $ 成正比例,$ y = y_1 + y_2 $,当 $ x = 2 $ 时,$ y = 9 $;当 $ x = 3 $ 时,$ y = 14 $。求 $ y $ 与 $ x $ 的函数表达式。
解:∵ $ y_1 $ 与 $ x + 1 $ 成正比例,∴设 $ y_1 = k_1(x + 1) $。
∵ $ y_2 $ 与 $ x - 1 $ 成正比例,∴设 $ y_2 = k_2(x - 1) $。
∵ $ y = y_1 + y_2 $,∴ $ y = k_1(x + 1) + k_2(x - 1) $。
∵当 $ x = 2 $ 时,$ y = 9 $;当 $ x = 3 $ 时,$ y = 14 $,
∴
$\begin{cases}3k_1 + k_2 = 9, \\4k_1 + 2k_2 = 14,\end{cases}$
解得
$\begin{cases}k_1 = 2, \\k_2 = 3.\end{cases}$
∴ $ y $ 与 $ x $ 的函数表达式为 $ y = 2(x + 1) + 3(x - 1) $,
即 $ y = $
解:∵ $ y_1 $ 与 $ x + 1 $ 成正比例,∴设 $ y_1 = k_1(x + 1) $。
∵ $ y_2 $ 与 $ x - 1 $ 成正比例,∴设 $ y_2 = k_2(x - 1) $。
∵ $ y = y_1 + y_2 $,∴ $ y = k_1(x + 1) + k_2(x - 1) $。
∵当 $ x = 2 $ 时,$ y = 9 $;当 $ x = 3 $ 时,$ y = 14 $,
∴
$\begin{cases}3k_1 + k_2 = 9, \\4k_1 + 2k_2 = 14,\end{cases}$
解得
$\begin{cases}k_1 = 2, \\k_2 = 3.\end{cases}$
∴ $ y $ 与 $ x $ 的函数表达式为 $ y = 2(x + 1) + 3(x - 1) $,
即 $ y = $
5x - 1
。答案:解:∵ $ y_1 $ 与 $ x + 1 $ 成正比例,∴设 $ y_1 = k_1(x + 1) $。
∵ $ y_2 $ 与 $ x - 1 $ 成正比例,∴设 $ y_2 = k_2(x - 1) $。
∵ $ y = y_1 + y_2 $,∴ $ y = k_1(x + 1) + k_2(x - 1) $。
∵当 $ x = 2 $ 时,$ y = 9 $;当 $ x = 3 $ 时,$ y = 14 $,
∴
$\begin{cases}3k_1 + k_2 = 9, \\4k_1 + 2k_2 = 14,\end{cases}$
解得
$\begin{cases}k_1 = 2, \\k_2 = 3.\end{cases}$
∴ $ y $ 与 $ x $ 的函数表达式为 $ y = 2(x + 1) + 3(x - 1) $,
即 $ y = 5x - 1 $。
∵ $ y_2 $ 与 $ x - 1 $ 成正比例,∴设 $ y_2 = k_2(x - 1) $。
∵ $ y = y_1 + y_2 $,∴ $ y = k_1(x + 1) + k_2(x - 1) $。
∵当 $ x = 2 $ 时,$ y = 9 $;当 $ x = 3 $ 时,$ y = 14 $,
∴
$\begin{cases}3k_1 + k_2 = 9, \\4k_1 + 2k_2 = 14,\end{cases}$
解得
$\begin{cases}k_1 = 2, \\k_2 = 3.\end{cases}$
∴ $ y $ 与 $ x $ 的函数表达式为 $ y = 2(x + 1) + 3(x - 1) $,
即 $ y = 5x - 1 $。
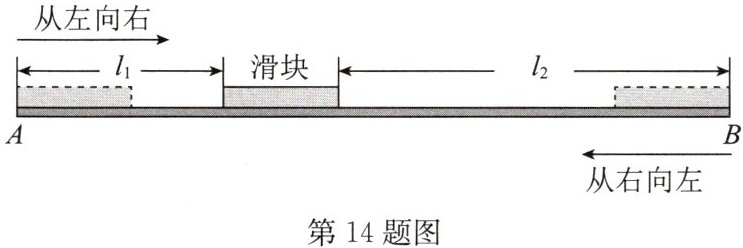
14. (2023·苏州)某动力科学研究院实验基地内装有一段笔直的轨道 $ AB $,长度为 1 m 的金属滑块在上面做往返滑动。如图,滑块首先沿 $ AB $ 方向从左向右匀速滑动,滑动速度为 9 m/s,滑动开始前滑块左端与点 $ A $ 重合,当滑块右端到达点 $ B $ 时,滑块停顿 2 s,然后再以小于 9 m/s 的速度匀速返回,直到滑块的左端与点 $ A $ 重合,滑动停止。设时间为 $ t(s) $ 时,滑块左端离点 $ A $ 的距离为 $ l_1(m) $,右端离点 $ B $ 的距离为 $ l_2(m) $,记 $ d = l_1 - l_2 $,$ d $ 与 $ t $ 具有函数关系。已知滑块在从左向右滑动过程中,当 $ t = 4.5 $ 和 5.5 时,与之对应的 $ d $ 的两个值互为相反数;滑块从点 $ A $ 出发到最后返回点 $ A $,整个过程总用时 27 s(含停顿时间)。请你根据所给条件解决下列问题:
(1) 滑块从点 $ A $ 到点 $ B $ 的滑动过程中,$ d $ 的值______
(2) 滑块从点 $ B $ 到点 $ A $ 的滑动过程中,求 $ d $ 与 $ t $ 的函数表达式;
(3) 在整个往返过程中,若 $ d = 18 $,求 $ t $ 的值。
(1) 滑块从点 $ A $ 到点 $ B $ 的滑动过程中,$ d $ 的值______
由负到正
;(填“由负到正”或“由正到负”)(2) 滑块从点 $ B $ 到点 $ A $ 的滑动过程中,求 $ d $ 与 $ t $ 的函数表达式;
(3) 在整个往返过程中,若 $ d = 18 $,求 $ t $ 的值。

答案:(1)由负到正
(2)解:设轨道 $ AB $ 的长为 $ n $ m,当滑块从左向右滑动时,
∵ $ l_1 + l_2 + 1 = n $,∴ $ l_2 = n - l_1 - 1 $,
∴ $ d = l_1 - l_2 = l_1 - (n - l_1 - 1) = 2l_1 - n + 1 = 2×9t - n + 1 = 18t - n + 1 $,∴ $ d $ 是 $ t $ 的一次函数。
∵当 $ t = 4.5 $ 和 $ 5.5 $ 时,与之对应的 $ d $ 的两个值互为相反数,∴当 $ t = 5 $ 时,$ d = 0 $,∴ $ 18×5 - n + 1 = 0 $,∴ $ n = 91 $,
∴滑块从点 $ A $ 到点 $ B $ 所用的时间为 $ (91 - 1)÷9 = 10 $(s)。
∵整个过程总用时 $ 27 $ s(含停顿时间),当滑块右端到达点 $ B $ 时,滑块停顿 $ 2 $ s,
∴滑块从 $ B $ 返回到 $ A $ 所用的时间为 $ 27 - 10 - 2 = 15 $(s)。
∴滑块返回的速度为 $ (91 - 1)÷15 = 6 $(m/s),
∴当 $ 12 ≤ t ≤ 27 $ 时,$ l_2 = 6(t - 12) $,
∴ $ l_1 = 91 - 1 - l_2 = 90 - 6(t - 12) = 162 - 6t $,
∴ $ d = l_1 - l_2 = 162 - 6t - 6(t - 12) = -12t + 234 $,
∴ $ d $ 与 $ t $ 的函数表达式为 $ d = -12t + 234 $。
(3)解:当 $ d = 18 $ 时,分两种情况:
由(2)可得,①当 $ 0 ≤ t ≤ 10 $ 时,$ 18t - 90 = 18 $,∴ $ t = 6 $;
②当 $ 12 ≤ t ≤ 27 $ 时,$ -12t + 234 = 18 $,∴ $ t = 18 $。
综上所述,当 $ t = 6 $ 或 $ 18 $ 时,$ d = 18 $。
(2)解:设轨道 $ AB $ 的长为 $ n $ m,当滑块从左向右滑动时,
∵ $ l_1 + l_2 + 1 = n $,∴ $ l_2 = n - l_1 - 1 $,
∴ $ d = l_1 - l_2 = l_1 - (n - l_1 - 1) = 2l_1 - n + 1 = 2×9t - n + 1 = 18t - n + 1 $,∴ $ d $ 是 $ t $ 的一次函数。
∵当 $ t = 4.5 $ 和 $ 5.5 $ 时,与之对应的 $ d $ 的两个值互为相反数,∴当 $ t = 5 $ 时,$ d = 0 $,∴ $ 18×5 - n + 1 = 0 $,∴ $ n = 91 $,
∴滑块从点 $ A $ 到点 $ B $ 所用的时间为 $ (91 - 1)÷9 = 10 $(s)。
∵整个过程总用时 $ 27 $ s(含停顿时间),当滑块右端到达点 $ B $ 时,滑块停顿 $ 2 $ s,
∴滑块从 $ B $ 返回到 $ A $ 所用的时间为 $ 27 - 10 - 2 = 15 $(s)。
∴滑块返回的速度为 $ (91 - 1)÷15 = 6 $(m/s),
∴当 $ 12 ≤ t ≤ 27 $ 时,$ l_2 = 6(t - 12) $,
∴ $ l_1 = 91 - 1 - l_2 = 90 - 6(t - 12) = 162 - 6t $,
∴ $ d = l_1 - l_2 = 162 - 6t - 6(t - 12) = -12t + 234 $,
∴ $ d $ 与 $ t $ 的函数表达式为 $ d = -12t + 234 $。
(3)解:当 $ d = 18 $ 时,分两种情况:
由(2)可得,①当 $ 0 ≤ t ≤ 10 $ 时,$ 18t - 90 = 18 $,∴ $ t = 6 $;
②当 $ 12 ≤ t ≤ 27 $ 时,$ -12t + 234 = 18 $,∴ $ t = 18 $。
综上所述,当 $ t = 6 $ 或 $ 18 $ 时,$ d = 18 $。