1. 若一次函数 $ y = kx - 5 $,当 $ x = - 2 $ 时,$ y = 7 $,则 $ k $ 的值是(
A. 6
B. - 1
C. - 6
D. 1
C
)A. 6
B. - 1
C. - 6
D. 1
答案:C
2. 如果 $ y $ 是 $ x $ 的正比例函数,$ x $ 是 $ z $ 的一次函数,那么 $ y $ 是 $ z $ 的(
A. 正比例函数
B. 一次函数
C. 正比例函数或一次函数
D. 不构成函数关系
B
)A. 正比例函数
B. 一次函数
C. 正比例函数或一次函数
D. 不构成函数关系
答案:B
3. 已知 $ y - 3 $ 与 $ x $ 成正比例,且当 $ x = 2 $ 时,$ y = 7 $,则 $ y $ 与 $ x $ 的函数表达式为(
A. $ y = 2x + 3 $
B. $ y = 2x - 3 $
C. $ y - 3 = 2x + 3 $
D. $ y = 3x - 3 $
A
)A. $ y = 2x + 3 $
B. $ y = 2x - 3 $
C. $ y - 3 = 2x + 3 $
D. $ y = 3x - 3 $
答案:A
4. 已知一次函数 $ y = kx + b $ 的图象经过点 $ ( - 1,2) $,且与 $ y $ 轴交点的纵坐标为 4,则该函数的表达式为
$ y = 2x + 4 $
。答案:$ y = 2x + 4 $
5. 一次函数 $ y = ax + 2 $ 的图象经过点 $ (1,0) $。当 $ y > 0 $ 时,$ x $ 的取值范围是
$ x < 1 $
。答案:$ x < 1 $
6. 当光线射到 $ x $ 轴时进行反射,如果反射光线经过点 $ A(0,1) $ 和点 $ B(3,4) $,那么入射光线所在直线的函数表达式为
$ y = -x - 1 $
。答案:1. 首先求反射光线所在直线的解析式:
设反射光线所在直线的解析式为$y = kx + b$。
因为反射光线经过$A(0,1)$和$B(3,4)$,把$A(0,1)$代入$y = kx + b$得$b = 1$。
把$B(3,4)$,$b = 1$代入$y = kx + b$得$4 = 3k + 1$,解得$k = 1$。
所以反射光线所在直线的解析式为$y = x + 1$。
2. 然后根据光的反射原理求入射光线:
设入射光线与$x$轴交点为$C$,因为反射光线与入射光线关于$x$轴对称。
反射光线$y = x + 1$与$x$轴交点$C$,令$y = 0$,则$0 = x + 1$,解得$x=-1$,即$C(-1,0)$。
点$A(0,1)$关于$x$轴的对称点$A'(0, - 1)$在入射光线上。
3. 最后求入射光线所在直线的解析式:
设入射光线所在直线的解析式为$y = mx + n$,把$A'(0, - 1)$,$C(-1,0)$代入$y = mx + n$。
把$A'(0, - 1)$代入得$n=-1$。
把$C(-1,0)$,$n = - 1$代入得$0=-m - 1$,解得$m=-1$。
所以入射光线所在直线的函数表达式为$y=-x - 1$。
设反射光线所在直线的解析式为$y = kx + b$。
因为反射光线经过$A(0,1)$和$B(3,4)$,把$A(0,1)$代入$y = kx + b$得$b = 1$。
把$B(3,4)$,$b = 1$代入$y = kx + b$得$4 = 3k + 1$,解得$k = 1$。
所以反射光线所在直线的解析式为$y = x + 1$。
2. 然后根据光的反射原理求入射光线:
设入射光线与$x$轴交点为$C$,因为反射光线与入射光线关于$x$轴对称。
反射光线$y = x + 1$与$x$轴交点$C$,令$y = 0$,则$0 = x + 1$,解得$x=-1$,即$C(-1,0)$。
点$A(0,1)$关于$x$轴的对称点$A'(0, - 1)$在入射光线上。
3. 最后求入射光线所在直线的解析式:
设入射光线所在直线的解析式为$y = mx + n$,把$A'(0, - 1)$,$C(-1,0)$代入$y = mx + n$。
把$A'(0, - 1)$代入得$n=-1$。
把$C(-1,0)$,$n = - 1$代入得$0=-m - 1$,解得$m=-1$。
所以入射光线所在直线的函数表达式为$y=-x - 1$。
7. (2024 春·常熟期末)如图,已知 $ B $ 中的实数与 $ A $ 中的实数之间的对应关系是某个一次函数。
(1) 若用 $ y $ 表示 $ B $ 中的实数,用 $ x $ 表示 $ A $ 中的实数,求 $ y $ 与 $ x $ 之间的函数表达式;
解:设一次函数表达式为 $ y = kx + b $,
把 $ (-3,9) $,$ (0,-3) $ 分别代入,得
$\begin{cases}-3k + b = 9, \\b = -3,\end{cases}$
解得
$\begin{cases}k = -4, \\b = -3,\end{cases}$
∴函数表达式为 $ y = $
(2) 求 $ m + n $ 的值。
解:在函数 $ y = -4x - 3 $ 中,当 $ x = -1 $ 时,$ y = 1 $,即 $ n = 1 $;
当 $ y = 5 $ 时,$ x = -2 $,即 $ m = -2 $,
∴ $ m + n = $
(1) 若用 $ y $ 表示 $ B $ 中的实数,用 $ x $ 表示 $ A $ 中的实数,求 $ y $ 与 $ x $ 之间的函数表达式;
解:设一次函数表达式为 $ y = kx + b $,
把 $ (-3,9) $,$ (0,-3) $ 分别代入,得
$\begin{cases}-3k + b = 9, \\b = -3,\end{cases}$
解得
$\begin{cases}k = -4, \\b = -3,\end{cases}$
∴函数表达式为 $ y = $
$-4x - 3$
。(2) 求 $ m + n $ 的值。
解:在函数 $ y = -4x - 3 $ 中,当 $ x = -1 $ 时,$ y = 1 $,即 $ n = 1 $;
当 $ y = 5 $ 时,$ x = -2 $,即 $ m = -2 $,
∴ $ m + n = $
$-1$
。答案:解:(1)设一次函数表达式为 $ y = kx + b $,
把 $ (-3,9) $,$ (0,-3) $ 分别代入,得
$\begin{cases}-3k + b = 9, \\b = -3,\end{cases}$
解得
$\begin{cases}k = -4, \\b = -3,\end{cases}$
∴函数表达式为 $ y = -4x - 3 $。
(2)在函数 $ y = -4x - 3 $ 中,当 $ x = -1 $ 时,$ y = 1 $,即 $ n = 1 $;
当 $ y = 5 $ 时,$ x = -2 $,即 $ m = -2 $,
∴ $ m + n = -2 + 1 = -1 $。
把 $ (-3,9) $,$ (0,-3) $ 分别代入,得
$\begin{cases}-3k + b = 9, \\b = -3,\end{cases}$
解得
$\begin{cases}k = -4, \\b = -3,\end{cases}$
∴函数表达式为 $ y = -4x - 3 $。
(2)在函数 $ y = -4x - 3 $ 中,当 $ x = -1 $ 时,$ y = 1 $,即 $ n = 1 $;
当 $ y = 5 $ 时,$ x = -2 $,即 $ m = -2 $,
∴ $ m + n = -2 + 1 = -1 $。
8. 当 $ x = 5 $ 时,一次函数 $ y = 2x + k $ 和 $ y = 3kx - 4 $ 的值相同,则 $ k $ 和 $ y $ 的值分别为(
A. 1,11
B. - 1,9
C. 5,15
D. 3,3
A
)A. 1,11
B. - 1,9
C. 5,15
D. 3,3
答案:A
9. 已知 $ y $ 是 $ x $ 的一次函数,下表中列出了 $ x $,$ y $ 的部分对应值,则 $ m $ 的值为(
| $ x $ | - 1 | 0 | 1 |
| --- | --- | --- | --- |
| $ y $ | 1 | $ m $ | - 1 |
A. - 1
B. 0
C. $ \frac{1}{2} $
D. - 2
B
)| $ x $ | - 1 | 0 | 1 |
| --- | --- | --- | --- |
| $ y $ | 1 | $ m $ | - 1 |
A. - 1
B. 0
C. $ \frac{1}{2} $
D. - 2
答案:B
10. (2024·宿城区期末)如图,在平面直角坐标系 $ xOy $ 中,$ O $ 为坐标原点,$ A(4,0) $,$ B(4,2) $,$ C(0,2) $,$ \triangle ODB $ 与 $ \triangle OAB $ 关于直线 $ OB $ 对称,$ OD $ 与 $ BC $ 交于点 $ E $,则 $ OD $ 所在直线的函数表达式为
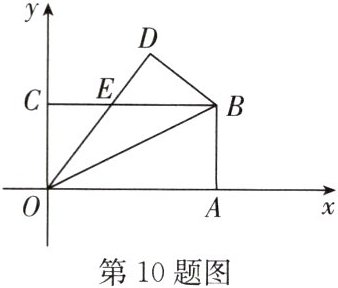
$ y = \frac{4}{3}x $
。
答案:1. 首先,根据已知条件判断四边形$OABC$的形状:
已知$A(4,0)$,$B(4,2)$,$C(0,2)$,$O(0,0)$,则$OA = 4$,$BC// OA$,$OC = AB=2$,$OC// AB$,所以四边形$OABC$是矩形。
因为$\triangle ODB$与$\triangle OAB$关于直线$OB$对称,所以$\angle DOB=\angle AOB$。
又因为$BC// OA$,所以$\angle EBO=\angle AOB$,则$\angle EBO=\angle DOB$,所以$OE = BE$。
2. 设$CE = x$:
因为$BC = 4$,$OC = 2$,$BE = OE=4 - x$。
在$Rt\triangle OCE$中,根据勾股定理$OC^{2}+CE^{2}=OE^{2}$,即$2^{2}+x^{2}=(4 - x)^{2}$。
展开$(4 - x)^{2}$得$16-8x + x^{2}$,则方程为$4+x^{2}=16 - 8x+x^{2}$。
移项可得:$8x=16 - 4$,即$8x = 12$,解得$x=\frac{3}{2}$。
所以$OE=4-\frac{3}{2}=\frac{5}{2}$,$E(\frac{3}{2},2)$。
3. 设$OD$所在直线的函数表达式为$y = kx(k\neq0)$:
把$E(\frac{3}{2},2)$代入$y = kx$中,得$2 = k×\frac{3}{2}$。
解得$k=\frac{4}{3}$。
所以$OD$所在直线的函数表达式为$y=\frac{4}{3}x$。
已知$A(4,0)$,$B(4,2)$,$C(0,2)$,$O(0,0)$,则$OA = 4$,$BC// OA$,$OC = AB=2$,$OC// AB$,所以四边形$OABC$是矩形。
因为$\triangle ODB$与$\triangle OAB$关于直线$OB$对称,所以$\angle DOB=\angle AOB$。
又因为$BC// OA$,所以$\angle EBO=\angle AOB$,则$\angle EBO=\angle DOB$,所以$OE = BE$。
2. 设$CE = x$:
因为$BC = 4$,$OC = 2$,$BE = OE=4 - x$。
在$Rt\triangle OCE$中,根据勾股定理$OC^{2}+CE^{2}=OE^{2}$,即$2^{2}+x^{2}=(4 - x)^{2}$。
展开$(4 - x)^{2}$得$16-8x + x^{2}$,则方程为$4+x^{2}=16 - 8x+x^{2}$。
移项可得:$8x=16 - 4$,即$8x = 12$,解得$x=\frac{3}{2}$。
所以$OE=4-\frac{3}{2}=\frac{5}{2}$,$E(\frac{3}{2},2)$。
3. 设$OD$所在直线的函数表达式为$y = kx(k\neq0)$:
把$E(\frac{3}{2},2)$代入$y = kx$中,得$2 = k×\frac{3}{2}$。
解得$k=\frac{4}{3}$。
所以$OD$所在直线的函数表达式为$y=\frac{4}{3}x$。